Аннотация
Показано, что ограниченный метод Харти-Фока (ОХФ) неустойчив по отношению к вариациям с переворотом спина для произвольного спина s ≠ 0 состояния. Введение ограничения спиновой чистоты на вариацию волновой функции устраняет эту универсальную нестабильность.
Введение
Имеются многочисленные указания на связь неустойчивости Хартри-Фока с реальными химическими явлениями [1,2]. Однако происхождение этой связи до сих пор остается неясным [3]. ВВозможно, это частично объясняется некоторой неполнотой самой теории устойчивости Хартри-Фока с открытыми оболочками. Так называемая нестабильность с переворотом спина [4], возникающая в результате вариаций занятых молекулярных орбиталей (МО) с противоположными спинами представляет собой один из таких примеров. Хотя гипотеза об ее общей природе была сделана на основе численного опыта в случае дублетных и триплетных состояний [2], строгого доказательства все еще нет. Причина в том, что нестабильность с переворотом спина возникает только во втором порядке по вариациям орбит, в отличие от более распространенных нестабильностей первого порядка с разными орбиталями для разных спинов (РОРС), и обычно полагают, что для этой ситуации необходимо было бы решать соответствующую задачу на собственные значения. Однако это не так, как будет показано в разделе 3, где доказана универсальная ОХФ-неустойчивость с переворотом спина для произвольного спина s ≠ 0, следующая непосредственно из выражения второй вариации энергии.
Ясно, что эта универсальная нестабильность не зависит от конкретной рассматриваемой системы и, следовательно, не может дать никакой физической информации. Она будет исключена в разделе 4 путем введения ограничения спиновой чистоты на вариацию полной волновой функции. Формализм матрицы плотности, кратко описанный для метода ОХФ с открытой оболочкой в разделе 2, используется повсюду. Благодаря своей инвариантности этот формализм особенно полезен в случае открытой оболочки, поскольку он позволяет одновременно рассматривать вариации и дважды, и однократно занятых орбиталей. Эти дополнительные преимущества лежат в основе простоты и краткости вывода.
Матрица плотности ОХФ и вариации энергии
Наша отправная точка – стандартный ОХФ определитель, построенный из дважды и однократно занятых орбиталей. Соответствующая матрица плотности, когда используются спиновые множители – это чистые α и β, хорошо известна [5]:
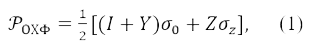
где I + Y и Z – матрица безспиновой и спиновой плотности, соответственно, I – единичная матрица, а σ – матрицы Паули. Удобство матрицы Y состоит в том, что указанные выше ограничения на орбитали оставляют Y как единственную независимую величину [6,7]:
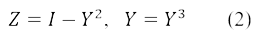
Оба соотношения легко проверяются в базисе МО, где Y и Z диагональны:
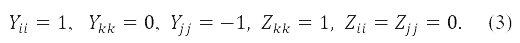
Собственные значения Y в (3) соответствуют числам заполнения 2, 1, 0 для дважды занятых, однократно заполненных и пустых МО, пронумерованных индексами i,k,j, соответственно.
Исходя с ОХФ волновой функции, мы рассмотрим наиболее общие вариации, которые нарушают свойство ОХФ, но сохраняют её одно детерминантную форму. В терминах вариации матрицы плотности δ𝒫 это означает, что
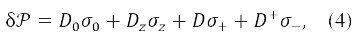
но 𝒫2 = 𝒫 и, следовательно, [2𝒫 - 1, δ𝒫]+ = 0. Последнее ограничение может быть переформулировано для бесспиновых компонентов δ𝒫 как [8,9]
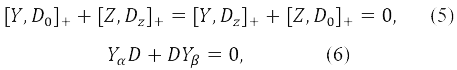
с помощью уравнений (1) и (4) и известных свойств матриц Паули. Здесь матрицы D0, Dz являются эрмитовыми, в то время как D может быть не эрмитовой, и D+ является эрмитово сопряженной матрице D. Для краткости мы продолжаем использовать символ Z для I - Y2 и ввели Yα = Y + Z, Yβ = Y - Z.
Матрицы D0, Dz относятся к обычным, различные орбитали для разных спинов (РОРС), вариациям молекулярных орбиталей (МО), в то время как матрица D соответствует вариации с переворачиванием спина, смешивающей МО со спином α и β. Как видно из уравнений (5) и (6) эти два вида искажения ОХФ волновой функции независимы друг от друга и могут быть рассмотрены отдельно. Это свойство остается также верным и для вариаций энергии. Энергия одно детерминантной волновой функции, построенной из спиновых орбиталей общего вида, были выражены через матрицу плотности 𝒫 с аналогичной (4) спиновой структурой,
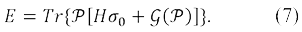
Для вариаций энергии легко заметить, что
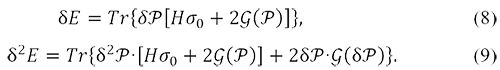
В уравнениях (7) – (9) 𝒢 обозначает усредненный оператор межэлектронного взаимодействия в спин-орбитальной форме. Его можно выразить через обычный Кулон-обменный, G, и обменный, K, операторы [8]. Например,
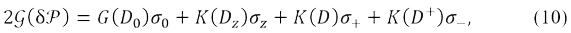
где G(A) и K(A) представлены в ортогональном базисе как
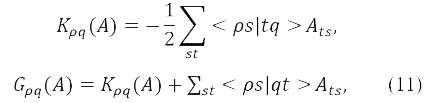
для произвольной матрицы A.
Универсальная нестабильность решения ОХФ с открытой оболочкой
Основными соотношениями в нашем рассмотрении проблемы устойчивости ОХФ с открытой оболочкой являются уравнения. (8) и (9), где 𝒫 должно быть равным 𝒫ОХФ из уравнения (1). Отсюда следует, что только вариации матрицы плотности РОРС, D0, Dz вносят вклад в δE. Полагая D0 = 0, можно показать, что δE = 2SpDzK(Z) где символ Sp, в отличие от Tr, не включает суммирование по спиновым переменным. Далее можно выбрать Dz = -kX, где k – малая положительная величина размерности (energy)-1
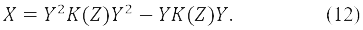
Таким образом, энергия уменьшается, δE = -kSpX2, и одновременно мы показали справедливость необходимого ограничения (5) на Dz поскольку [Y,X]+ = ZX = XZ = 0. Этот результат [10] распространяет на произвольный ненулевой спин доказательство [11] неустойчивости ОХФ решения относительно РОРС состояния, полученное ранее для дублетов. В частности, результаты полученные с помощью уравнений (3), (11) и (12) естественно обобщают уравнение (4) в статье [4]
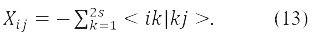
Для вариаций с переворотом спина единственная ненулевая матрица в уравнении (4) это D. Тогда δE обращается в ноль, и вариация энергии второго порядка δ2E необходима для решения проблемы стабильности. После редукции (свёртки) спинов уравнение (9) можно представить в виде
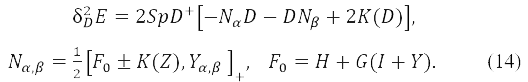
При выводе уравнения (14) условие (6) и соотношение δ2𝒫 = 2(δ𝒫)2 - 4𝒫(δ𝒫)2 были учтены.
Последнее верно, что можно проверить для матрицы 𝒫 Фока-Дирака, когда спин-орбитальные вариации ортогональны занятым спин-орбиталям. Но даже при этом ограничении теперь показано, что ОХФ решение всегда нестабильно к переворачиванию спина. Другими словами, можно выбрать какое-то конкретное D, для которого δ2DE < 0. Положим D = aZ+ kX, где a – малое безразмерное число, и найдем
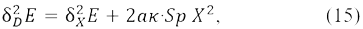
с учетом тождеств YZ = ZX = XZ = [Y,X]+ = 0, следующих из (2) и (12). Ясно, что если X ≠ 0, то δ2DE < 0 для a < -kδ2XE/2Sp(kX2) (в первом порядке как по a, так и по k). Ч.Т.Д.
Оставшаяся возможность X = 0 допускает более слабое неравенство δ2DE ≤ 0 = δ2aZE. Из-за ограничений симметрии патологический случай X = 0 иногда возникает в реальных расчетах [1,4] в результате использования минимального базисного набора. Достаточное расширение базиса всегда приводит к появлению пустой орбитали j, имеющей ту же симметрию, что и некоторая дважды занятая орбиталь i. Затем, согласно (13), X ≠ 0 и δ2 E < 0. Аналогичное изменение симметрии уровней может также случиться в минимальном базисе в точке пересечения орбитальной энергии [1], где пустая орбиталь j в уравнении (13) становится симметричной и появляется ненулевой интеграл <ik|kj>. В результате как РОРС, так и нестабильность с переворотом спина для ОХФ волновой функции возникают одновременно с матрицей X отличной от нуля.
Устойчивость при ограничении спиновой симметрии
В случае ОХФ естественно классифицировать вариации D с переворотом спина не только по изменению ΔM в проекции полного спина вариации δ&Ψ волновой функции, но также и по значению полного спина. Анализ показывает, что соответствующие ограничения на матрицу D для ΔM = -1 и произвольных Δs:
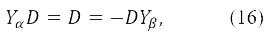
тогда, как для ΔM = Δs = 1,
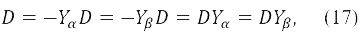
и для ΔM = Δs = -1,
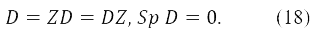
Приведенное выше доказательство неустойчивости переносится на случай ΔM = -1. Действительно, вывод неравенства δ2E < 0 здесь подробно следует выводам из раздела 3, если пробная матрица D выбрана в форме aZ + k(X + YX), удовлетворяющей уравнению (16). Следовательно, неустойчивость с переворотом спина зависит от примеси функций произвольных Δs и ΔM = -1 в δΨ. Ключевую роль в этой примеси играет функция S--Ψ0, принадлежащая тому же мультиплету Ψ0. Поскольку все функции некоторого мультиплета вырождены, можно гарантировать по крайней мере: δ2E = 0. Такой же вывод в отношении использованных выше матриц следует из тождества δ2ZE = 0. Заметим, что матрица спиновой плотности Z является также пространственной частью матрицы плотности перехода между Ψ0 и S-Ψ0. Другое определяющее значение X, следует из искажений замкнутой оболочки, дающем строгое неравенство δ2E < 0.
Чтобы прояснить источник установленной неустойчивости, рассмотрим трех электронный пример. Такая ОХФ функция Ψ0 = det[χα,χβ,φα]/61/2 после вариации с поворотом спина превращается, в
Ψ = det[χα+αψβ,χβ,φα+bφβ]/ [6(1+a2)(1+b2)]1/2,
где χ, φ, ψ – некоторые ортогональные орбитали. Линейная компонента δΨ, которая содержит a и b, от Ψ состоит S-Ψ0 = det[χα,χβ,φα]/61/2 и Ψ1 = det[ψβ,χβ,φα]/61/2. В выражении энергии E = <Ψ|H|Ψ> эти члены взаимодействуют друг с другом, но не с Ψ0 для бесспинового Гамильтониана H. Таким образом, до низшего порядка по a и b
E = E0 + a2(E1 - E0) - ab <χφ|φψ>,
где E = <Ψ0|H|Ψ0>, E1 = <Ψ1|H|Ψ1>. Ясно, что E < E0 получается подходящим выбором малых чисел a и b. Видно, что одновременное изменение однократно и двукратно заполненных МО является существенной особенностью нашего доказательства, тогда как в существующем выводе [12] уравнений вековой неустойчивости с переворотом спина такие вариации рассматриваются отдельно.
Однако наше настоящее доказательство не может быть перенесено на матрицы D, которые подчиняются уравнениям. (17) и (18), поскольку эти ограничения исключают D = aZ из множества допустимых матриц вследствие свойств YαZ = Z, Sp Z = 2s (см. уравнения (2) и (3)). В результате в этих случаях мы должны решать задачи на собственные значения, связанные с (14)
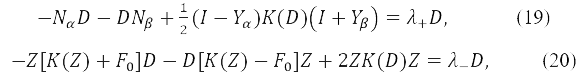
для Δs = ΔM = 1 и ΔM = Δs = -1 соответственно. Левые части этих уравнений являются проекциями, в терминах скобок в уравнении (14), на подпространства D-матриц, удовлетворяющих уравнениям (17) и (18). В заключение, следует подчеркнуть, что в этих случаях сохранение квадрата полного спина решает проблему устойчивости, она становится эквивалентной определению наименьшей энергии перехода в базисе всех однократно возбужденных конфигураций. Действительно, различие между этими двумя задачами на собственные значения обусловлено тем, что матричный элемент <δ2Ψ1|H|Ψ0> входит в δ2E. Дважды возбужденные конфигурации, образующие δ2Ψ, могут соответствовать либо ΔM = ±2, либо ΔM = 0, определяемых возбуждениями с переворотом спина. Первые не взаимодействуют с Ψ0, в то время как последние (вторые) вообще не появляются в δ2Ψ, когда на δΨ накладывается ограничение ΔM = ±1.
Обсуждение
Любое приближенное решение уравнения Шредингера «неустойчиво» по отношению к более точному. Это тривиальное замечание показывает, что такого рода нестабильность не может дать конкретной информации для частной системы. Как было продемонстрировано, все варианты неустойчивости указанного выше типа в случае ОХФ связаны с единственной ненулевой матрицей X (уравнение (12)), которая определяет направление, а также величину сдвига [13] от ОХФ, к более точной неограниченного Хартри – Фока (НХФ) волновой функции, и, одновременно, к еще более точной спин расширенной волновой функции, описывающей то же состояние. Поэтому в рамках ОХФ естественно исключить эти внешние нестабильности из рассмотрения. Тогда единственные уравнения устойчивости (19) и (20) и уравнения внутренней RHF устойчивости (65) из ссылки [10] остаются. Все они гарантируют сохранение спина и, следовательно, могут указывать на фактическое пересечение потенциальных гиперповерхностей разных состояний с одинаковой или разной мультиплетности. В последнем случае наименьшее собственное значение нестабильности совпадает с энергетическим разделением соседних низколежащих гиперповерхностей, вычисленных посредством суперпозиции всех однократно возбужденных конфигураций.
Таким образом, после устранения универсальной нестабильности, присущей любому приближенному решению, описание химического феномена в рамках теории нестабильности сведена, фактически, к определению пересечения энергетических уровней. Возможно, наиболее интересная проблема появления новых состояний, обусловленная межэлектронным взаимодействием, может быть исследована в рамках ОХФ метода, применением, учётом, порога его внутренней нестабильности так же, как и в случае замкнутой оболочки [14,15].
Список использованной литературы
1. K. Yamaguchi and H. Fukutome, Progr. Theor. Phys. Phys. 54 (1975) 1599.
2. K. Yamaguchi, Chem. Phys. 29 (1978) 117.
3. H. Fukutome, Intern. J. Quantum Chem. 20 (1981) 955.
4. K. Yamaguchi and T. Fueno, Chem. Phys. Letters 38 (1976) 47
5. R. McWeeny and B.T. Sutcliffe. Methods of molecular quantum mechanics (Academics Press, New York,
1969).
6. G.G. Bollini, J.J. Giambiagi, M. Giambiagi and M.S. de Giambiagi, Theoret. Chim. Acta 22 (1971) 234.
7. M.M. Mestechkin and G.E. Whyman, Intern. J. Quantum Chem. 8 (1974) 45.
8. A.V. Luzanov and M.M. Mestechkin, Teor. Ecsp. Khim. 8 (1972) 435.
9. H. Fukutome, Progr. Theor. Phys. 52 (1974) 115.
10. M.M. Mestechkin, Intern. J. Quantum Chem. 13 (1978) 469.
11. J. Paldus and J. ?i?ek, J. Chem. Phys. 52 (1974) 1766.
12. K. Hirao and H. Nakatsuji , J. Chem. Phys. 69 (1978) 4548.
13. G.E. Whyman and M.M. Mestechkin, Teor. Ecsp. Khim. 18 (1982) 723.
14. H. Fukutome, Progr. Theor. Phys. 53 (1975) 1320.
15. M.M. Mestechkin, Intern. J. Quantum Chem. 15 (1979) 601.