Материал сайта http://www.eidos.ru

Развитие интеллектуальной одаренности и творческих способностей учащихся в условиях научного общества учащихся

Маслова Вера Алексеевна, учитель математики, руководитель методического объединения математиков МОУ СОШ № 65, г. Воронеж

Среди школьных предметов математика занимает совершенно особое место. Весьма немногочисленную группу учеников составляют математические вундеркинды, учащиеся-звезды, победители олимпиад высокого уровня. Представители этой группы овладевают школьной программой «играючи». Их математические аппетиты требуют все новой и новой пищи. Им интересно изучать то, «что в школе никто не изучает». В работе с этими учениками важно не навредить, не помешать.

Возможно ли по поведению ребенка определить, что он талантлив?

Не существует модели одаренного ребенка и не существует специальных критериев, определяющих способности детей.

Проблема одаренности - это проблема личности. Если ребенок отличается от сверстников богатством своих эмоциональных состояний, неуправляемостью, повышенной любознательностью, неусидчивостью и бунтарством, независимостью поведения, честолюбием и усиленной потребностью в самовыражении, на него необходимо обратить внимание.

Исследования психологов показывают, что одаренные дети в школе зачастую имеют репутацию «непослушных», «странных» и даже «слабоумных» среди учителей и сверстников. Они не умеют приспосабливаться к традиционной системе обучения, т.е. быть как все, ведь они по каждому вопросу имеют свое собственное мнение и не скрывают его.

Что хочет одаренный ребенок - загадка для многих взрослых. Такой ребенок всегда индивидуальность, а индивидуальность всегда имеет свои пути в решении задач, уклоняясь от общих требований.

Не существует стандартной технологии, которая бы развивала ребенка, так как школьная система построена на общественной требовательности, обучение стандартизировано. В обучении есть общая цель, но у каждого ученика есть и частная цель обучения. Чаще всего появляется сталкивание этих целей, возникают противоречия. К сожалению, часто нестандартные дети «не вписываются» в систему государственной школы.

Данные, приводимые социологами, просто кричащие: 30% сверходаренных детей отчисляются из школы за неуспеваемость, 2/3 одаренных детей скрываются под личиной интеллектуальных саботажников, а процент самоубийств среди них выше в 2 раза. Это крик ребенка, который не смог адаптироваться к общепринятым стандартам.

Проблема взращивания одаренного ученика начинается с проблемы обучения одаренного учителя. Нередко педагог стремится сделать всех одноклассников одинаковыми, подстроить каждого под так называемого среднего ученика. И способные дети в таких условиях либо гаснут и становятся совсем неплохими дисциплинированными мальчиками и девочками, либо вопреки школе становятся Сахаровыми, Курчатовыми, Эйнштейнами. Вера учителя в ученика раскрывает в последнем множество возможностей. Равнодушие и невнимание - самое большое зло для всех детей. Помочь ребенку найти себя, а потом всячески поддерживать его - великая миссия настоящего учителя. Необходимо создать условия, в которых все дети могли бы реализоваться.

И вот эта-то задача, пожалуй, самая трудная для взрослых. Я бы назвала ее даже не задачей, а мечтой - той самой мечтой, без воплощения которой жизнь не может стать счастливой.

Как обучать одаренных детей?

Россия одаренными детьми занималась в начале прошлого века (недолго до 1936 года), а затем не занималась вообще, следовательно, научной школы нет, она только зарождается. Американцы за последние 90 лет разработали много моделей работы с одаренными детьми, эти модели и легли в основу разработок российских ученых. Среди этих моделей доминирует интеллектуальная одаренность. Здесь существует две стратеги обучения:
•  Акселерация (или ускоренный курс);
•  Расширенное обучение.

Интеллектуально одаренные дети обладают:
A) с хорошей памятью;
Б) с высокой способностью концентрации внимания;
B) с высоким уровнем воображения и фантазии;
Г) с высоким уровнем «достиженчества».

В нашей школе применяется стратегия расширенного обучения, то есть формируем профильные классы, если дети имеют способности по определенным предметам, а не вообще. Это: математический, химико- биологический, гуманитарный и т.д., а также осуществляем расширенное обучение детей по отдельным областям знания, организуя факультативы, спецкурсы, элективные курсы, кружки, а также научные общества учащихся по различным предметам.

Учение - это целенаправленный и мотивированный процесс, поэтому задача учителя состоит в том, чтобы включить каждого ученика в деятельность, обеспечивающую формирование и развитие познавательных потребностей.

Научное математическое общество (НМО) существует в школе № 65 семь лет. Оно объединяет учеников 7 - 10 классов, интересующихся математикой, склонных к исследовательской работе и имеющих нестандартное мышление. Руководителем общества является учитель, работающий в математическом классе.

Члены научного математического общества под руководством учителя проводят исследовательскую работу, это позволяет не развивать личность вообще, а развивать ее на конкретном материале. Этому процессу способствует осознание учеником цели предстоящей деятельности. Цепочка, по которой происходит этот процесс, выглядит так: потребность — мотив — цель — действие — рефлексия (самоанализ собственной деятельности).

Руководитель учит на семинарах детей оформлять рефераты и доклады по теме, вместе с учащимися подбирает литературу, проводит консультации, учит детей владению методикой эксперимента.

При организации деятельности учащихся в научном математическом обществе учитель переходит с позиций носителя знаний (дающего знания) в позицию организатора собственной познавательной деятельности учащихся, т.е. учитель управляет познавательной деятельностью ученика, создает ситуацию успеха, разрабатывает с учеником «самостоятельное открытие» математической закономерности, вызывающее положительные эмоции.

При организации работы в начале года ученики выбирают определенную тему для исследовательской работы в течение хода. Затем учащиеся появившуюся гипотезу воплощают в проект, занимается решением проблемы, поставленной перед ними, воплощают проведенные исследования в законченную работу. Вся работа проводится по следующей схеме:

Схема условна, но может иметь непосредственное реальное воплощение в процессе деятельности учащихся. В соответствии с ней деятельность школьников по изучению теории может быть организована так:

Таким образом, дети, выбирая «узкую» тему, проводят глубокое исследование ее и в конце учебного года защищают полученные результаты на общешкольной научной конференции. При этом выбор тем исследования происходят по желанию учащихся, но при условии практической значимости, наличии литературы, возможности многопланового исследования темы.

Цель работы научного общества математиков заключается в поиске будущих математиков. Задача НМО - обеспечить поэлементное усвоение опыта творческой деятельности (умение видеть проблему, высказывать предложение, формировать гипотезы, давать определения понятиям, строить доказательство, делать выводы). В итоге, все это должно привести к исследовательской практике, что, как известно, является основным методом обучения творческой деятельности. Ученик постепенно превращается из слушателя в собеседника, а затем в исследователя и на доступном ему уровне включается в учебно- исследовательскую, творческую работу.

В результате творческой деятельности у учащихся появляется интерес к математике. Ученик чувствует эстетическое удовлетворение от красиво решенной задачи, от установленной им возможности приложения математики к другим наукам.

Рассмотрим в качестве примера открытый урок по геометрии в 11 классе на тему «Конус, площадь его поверхности и объем»

“Проблемы нам создают не те вещи,
которые мы не знаем, а те, о которых
мы ошибочно полагаем, что знаем”
В. Роджерс

Цель урока: Систематизация и углубление знаний по теме “Конус”. Повысить интерес к геометрии, решая нестандартные задачи и отвечая на занимательные вопросы. Создание положительной внутренней мотивации обучения учащихся.

Ход урока.

I. Вопросы к классу с комментариями учителя:

1. Сегодня на уроке мы обобщим и систематизируем свои знания по теме “Конус”, повторим основные формулы и применим их при решении практических задач.
Вы должны были повторить основные понятия по теме и установить связь между картиной Шишкина “Корабельная роща” и геометрическим телом, которое называется “конус”. Кто из Вас нашел эту “связь”? (Учитель демонстрирует репродукцию картины).

Ответ: Конус в переводе с греческого языка означает “сосновая шишка”, а на картине изображен сосновый лес.

2. Фронтальная работа с классом по основным понятиям темы. Два ученика решают задачи на доске по карточкам.

Вопросы к классу:
•  Дайте определение конуса;
•  Какая поверхность называется конической;
•  Назовите элементы конуса и покажите их на чертеже;
•  Какой конус называется прямым?
•  Запишите формулы объема конуса, площади боковой и полной поверхности конуса.

3. Проверка задач, решенных учениками на доске:

Задача 1. Радиус основания конуса R. Осевым сечением является прямоугольный треугольник. Найти его площадь.

Задача 2. Осевым сечением конуса является равнобедренный прямоугольный треугольник, площадь которого 9 м² . Найти объем конуса.

4. Самостоятельная работа на 2 варианта с последующей проверкой (два ученика решают на закрытых досках).

Вариант I. Найдите высоту конуса, если его объем равен 48 pi см³, а радиус основания 4 см.

Вариант II. Найдите радиус основания конуса, если его объем равен 2,25 pi см ³ , а высота 3 см.

5. Решить задачу: Образующая конуса равна 18 см и наклонена к плоскости основания под углом 60° . Найдите площадь осевого сечения, площадь полной поверхности конуса и его объем.

II. Примените полученные знания на практике.

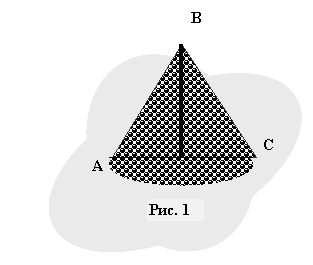
Комментарии учителя : Итак, Вы уже знаете, как найти элементы конуса, его поверхность и объем, но сможете ли Вы применить эти знания, выходя на “вольный воздух”. Ведь куча щебня по краям шоссейной дороги также представляет предмет, заслуживающий внимания. Посмотрев на рисунок 1, мы можем задать себе вопросы:
•  Какую площадь занимает щебень?
•  Какова поверхность этой кучи щебня?
•  Каков её объем?

Задачи довольно сложные для человека, привыкшего преодолевать математические трудности только на бумаге или на классной доске. Ведь необходимо вычислить объем и поверхность конуса, высота и радиус которого не доступны для непосредственного измерения. Вопросы к классу:
•  Как найти радиус?
(измерить окружность основания и разделить на 6,28 = 2 pi );
•  Как найти образующую?
(определить две образующие: перекинув метровую ленту через вершину кучи);
•  Как найти высоту?
(определить по теореме Пифагора).

Задача: Пусть окружность конической кучи щебня 12 м. Длина двух образующих – 4,6 м. Найти площадь поверхности кучи щебня и её объем.

Решение.

l = 4,6 / 2 = 2,3 м

r = 12,1 / 6,28 = 1,9 м

S = pi *r*l = 3,14 * 1,9 * 2,3 = 13,7 м ²

V = 1/3* p * r² * H = 1/3*3,14*1,9 ² * = 1/3*3,14*3,61* = 1/3*3,14*3,61* =1/3*3,14*3,61*1,3 = 4,9 м ³

Комментарии учителя: При взгляде на коническую кучу щебня или песка мне вспоминается старинная легенда восточных народов, рассказанная у А.С. Пушкина в “Скупом рыцаре”. Послушайте её:

“Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу,-
И гордый холм возвысился,
И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли”.

Какие ассоциации вызывают у Вас эти стихи ?

Холм – конус.
Какого объема может быть этот холм ?
Какой высоты мог быть этот холм ?
На сколько километров может увеличиться панорама для наблюдения, поднявшегося с подножия холма к его вершине ?

Давайте попытаемся ответить на эти вопросы и проанализировать этот текст (три ученика заранее подготовили ответ).

Первый ученик рассказывает. Это одна из тех немногих легенд, в которых при кажущемся правдоподобии нет и зерна правды. Дело в том, что если какой-нибудь древний деспот вздумал бы осуществить такую затею, то он был бы обескуражен мизерностью результата: перед ним высилась бы настолько жалкая кучка земли, что никакая фантазия не в силах была бы раздуть в легендарный, “гордый холм”. Сделаем примерный расчет: Старинные армии были не так многочисленны, как в наше время. У Аттилы было самое многочисленное войско, какое знал древний мир. Историки оценивают его в 700 тысяч человек.

Остановимся на этом числе, то есть примем, что холм составился из 700000 горстей. Захватите самую большую горсть земли и насыпьте в стакан: Вы не наполните его одной горстью. Все же примем, что горсть древнего воина равнялась одному стакану, примерно 1/5 литра или 1/5 куб. дм.

Определим объем холла: (1/5)*700 000 = 140000 куб. дм. = 140 куб. м. Значит холм представлял собой конус объемом не более 140 куб. м. Такой скромный объем уже разочаровывает.

Учитель: Но продолжим расчеты. Найдем высоту этого холма.

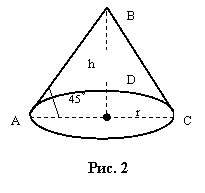Второй ученик рассказывает: Чтобы определить высоту холма, нужно знать какой угол составляет образующая конуса с его основанием. В нашем случае можно принять его равным углу естественного откоса, то есть 45° (рис. 2). Более крупных склонов нельзя допустить, так как земля будет осыпаться. Остановившись на угле в 45° , рассмотрим треугольник АВС.

Высота такого конуса равна радиусу его основания. h = R; V = 140 м ³;

V = (1/3)*S*h = (1/3)* p *R ² *h =

(1/3)* pi *h 3 ; 140 = (1/3)* pi *h³ ;

pi *h³ = 420; h³ = 133,76; h = 5,1 м .

В результате вычислений получили, что при объеме холма 140 м³, высота его составляет 5,1 м. Сомнительно, чтобы курган подробных размеров мог удовлетворять честолюбие Аттилы. С таких небольших возвышений легко было бы видеть дол, покрытый белыми шатрами, но обозревать море, было бы возможно только если дело происходило невдалеке от берега.

Учитель: Итак, ответили на один вопрос, но остается еще вопрос, возникший у нас : как далеко можно видеть с той или иной высоты?

Посмотрите на рисунок 3.

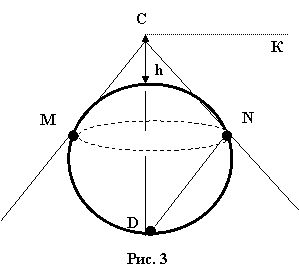Третий ученик рассказывает. Ответим на вопрос, как велик радиус круга, в центре которого видим себя на ровной местности или на высоте. Задача сводится к вычислению длины отрезка СN касательной, проведенной из точки на уровне глаза наблюдателя к земной поверхности.

Пусть h – рост наблюдателя (внешний отрезок секущей); R – радиус Земли равный 6400 км. (h + 2R) – длина секущей CD, тогда СN² = h*(h + 2R). Так как рост человека мал по сравнению с R, то h + 2R = 2R, следовательно СN² = h*2R. Рост человека до глаз примерно h = 1,6 м или 0,0016 км, тогда СN = = = 80* = 4,52 км.

Воздушные облака Земли искривляют путь лучей и горизонт отодвигает на 6%, тогда дальность видимости будет соответствовать 4,52*1,06 = 4,8 км, то есть на ровном месте человек видит не далее 4,8 км. Это гораздо меньше, чем обычно думают люди, которые описывают дальний простор степей, окидываемых взглядом.

Cходную ошибку делает А.С. Пушкин, говоря в “Скупом рыцаре” о далеком горизонте.

Мы нашли, что высота холма приблизительно 5 метров. Если наблюдатель встал на вершину конического холма, то глаз его возвысился бы над почвой на 6.6 км. В этом случае дальность горизонта была бы равна = 9 км. Это всего на 4 км больше того, чем можно видеть, стоя на ровной земле.

---

Для ссылок:
Маслова В. А. Развитие интеллектуальной одаренности и творческих способностей учащихся в условиях научного общества учащихся // Интернет-журнал "Эйдос". - 2007. - 15 января. http://www.eidos.ru/journal/2007/0115-6.htm. - В надзаг: Центр дистанционного образования "Эйдос", e-mail: list@eidos.ru.