МОДЕЛИРОВАНИЕ ДВУХМАССОВЫХ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ С УЧЕТОМ ЗАЗОРА В КИНЕМАТИЧЕСКОЙ ПЕРЕДАЧЕ
Тищенко А.А., студент
5-го курса, Толочко О.И., к.т.н., доц.
Донецкий государственный
технический университет
toi@elf.dgtu.donetsk.ua
Многие электромеханические
системы исполнительный механизм-двигатель
могут быть представлены в виде двух сосредоточенных
масс с моментами инерции J1, J2,
связанных между собой безынерционной упруго-вязкой
кинематической передачей с коэффициентом
упругости c12, коэффициентом вязкого
трения b12 и зазором d,
обусловленным неточностью изготовления
или износом узлов передачи [1].
Структурная схема
такой двухмассовой электромеханической
системы (ДЭМС) без учета моментов сухого
трения, воздействующих на сосредоточенные
массы, представлена на рис. 1, где обозначены w1, w2 – угловые скорости двигателя и механизма,
M – электромагнитный момент двигателя,
MC – момент сопротивления механизма,
MУ, MВ и M12 – упругий, вязкий
и упруго-вязкий моменты, Dw, Dj – скорость и угол скручивания передачи
(все величины и параметры механизма и кинематической
передачи приведены к валу двигателя). Типовая
нелинейность "зона нечувствительности"
моделирует зазор в передаче, обеспечивая
наличие упругого и вязкого моментов только
после выбора зазора: ïDj0+Djï³d/2,
где ïDj0ï£d/2 – начальное значение координаты Dj.
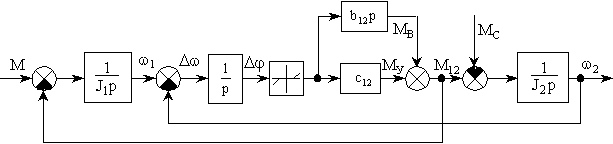
Рисунок 1
Существенным недостатком
этой структуры является наличие звена
чистого дифференцирования, которое не
может быть исключено из модели простым
переносом параллельной связи на вход интегратора,
как это делается при отсутствии зазора
в передаче. Этого недостатка лишена предлагаемая
модель ДЭМС, представленная на рис. 2. Исключение
операции чистого дифференцирования здесь
оказалось возможным за счет включения
следующих нелинейных звеньев: выделение
модуля, знаковая функция и блок умножения.
Эти звенья легко реализуются как на аналоговых,
так и на цифровых вычислительных машинах
и не вносят погрешностей, связанных с численным
дифференцированием или заменой идеального
дифференцирования реальным (включением
апериодического звена с постоянной времени,
намного меньшей постоянной времени дифференцирования).
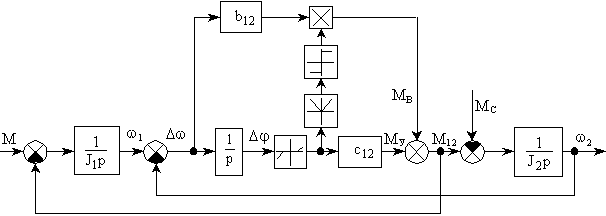
Рисунок 2
Моделирование на ЭВМ
в среде приложения Simulink пакета
Matlab
показало идентичность динамических свойств
рассматриваемых моделей (рис. 1 и 2). На рис.
3 показаны графики переходных процессов
в системе рис. 2 при d=1°
(MН – номинальный момент двигателя).
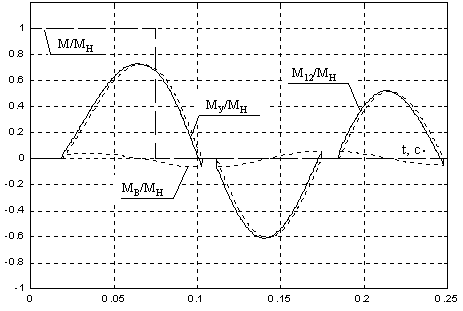
Рисунок 3
ЛИТЕРАТУРА
- Башарин А. В., Новиков
В. А., Соколовский Г. Г. Управление электроприводами:
Учебное пособие для вузов. – Л.: Энергоиздат.
Ленингр. отд-ние, 1982. - 392 с.
Ольга
Толочко, Артем Тищенко. Моделирование двухмассовых
электромеханических систем с учетом зазора
в кинематической передаче / Тези доповідей
міжнародної науково-технічної конференції,
м. Львів, 1999. - с. 265-266.
НАЗАД
НА ПУБЛИКАЦИИ
©
Тищенко А.А., 2000.



