
 |
Статья в сборник ДонГТУ, 2000 г. |
ПОВЫШЕНИЕ ТОЧНОСТИ УСОВЕРШЕНСТВОВАННОГО
ГРАДИЕНТОМЕТРИЧЕСКОГО МЕТОДА ИЗМЕРЕНИЯ ПРОФИЛЕЙ ТЕМПЕРАТУР
Ефименко Е. И., Зори А. А.,Ким Нарзан
Для уменьшения динамической погрешности измерения температур градиентометрическим методом при контактном зондировании морской среды был разработан усовершенствованный градиентометрический метод [1]. В нем применены коррекции для уменьшения статической и динамической составляющих погрешности, присущих градиентометрическому методу измерения профилей температур. При коррекции статической составляющей погрешности [1] автор принял гипотезу о линейном законе ее распределения по глубине. Согласно этой гипотезе, коррекцию температуры в зоне термоклина выполняют в соответствии с выражением:
 |
(1) |
где Ткстi— скорректированное значение
температуры на i-ом шаге с учетом накопленной
статической составляющей погрешности D
К в зоне термоклина;
hn, ha— глубины начала и конца
термоклина.
С целью повышения точности коррекции погрешности нами предложено принять гипотезу о степенном законе распределения статической составляющей этой погрешности по глубине с определением оптимального показателя степени. При этом коррекцию температуры в зоне термоклина следует выполнять согласно выражению
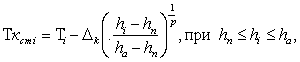 |
(2) |
где р – некоторое рациональное число.
С целью подтверждения правильности
предложенной гипотезы и оценки эффективности
нового метода коррекции накапливаемой
статической составляющей погрешности,
определяемой степенью снижения погрешности
измерения профилей температур по отношению к
известному методу, предложенному в [1], проведено
имитационное моделирование с помощью
прикладного математического пакета MATHCAD 7.0. При
оценке эффективности коррекции использовалась
методика, изложенная в [2]. Погрешность измерения
профилей температур определяется степенью
отклонения скорректированного соответствующим
методом измеренного профиля с учетом
инерционных свойств измерительного канала, по
отношению к истинному профилю, который
устанавливается при моделировании в
соответствии с его теоретической моделью. Как
показали результаты исследований, степень
отклонения скорректированного и истинного
профилей температур при градиентометрическом
методе измерений тем больше, чем больше разность
постоянных времени датчиков t 1 и t 2 измерительных
каналов температуры, образующих градиентомер.
Сравнение результатов моделирования при
рассогласованиях постоянных времени датчиков на
10%, 15%, 20%, 25%, что реально имеет место, для
предложенной гипотезы о степенном законе
распределения по сравнению с линейным законом
позволило констатировать уменьшение
погрешности измерения профилей температур, как
минимум в 1,5…2 раза. Как показали результаты
моделирования, значение оптимального показателя
степени полинома, характеризующего максимальное
приближение скорректированного профиля с
истинным и обеспечивающего минимальную
погрешность, зависит от степени рассогласования
постоянных времени измерительных каналов
температур градиентомера D t /t СР
=(t 2-t 1)/t СР . Это требует,
при применении нового метода, их предварительной
оценки. При моделировании, для сравнительной
оценки использованы профили температур,
приведенные в [1]. На рис. 1 представлена
зависимость математического ожидания (МО)
абсолютной погрешности измерения профиля
температуры ![]() , определяемого
средним значением разности температур для
модели истинного профиля и профиля после
коррекции статической составляющей погрешности,
от показателя степени р. Моделирование
проводилось при 20% отклонении постоянных времени
датчиков от номинального значения t
Н=0,3с (t1 =0,27с и t2 = 0,33с).
, определяемого
средним значением разности температур для
модели истинного профиля и профиля после
коррекции статической составляющей погрешности,
от показателя степени р. Моделирование
проводилось при 20% отклонении постоянных времени
датчиков от номинального значения t
Н=0,3с (t1 =0,27с и t2 = 0,33с).
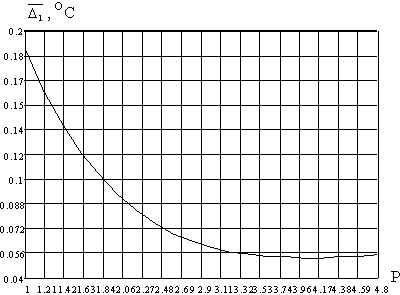 |
Рисунок 1– Распределение МО абсолютной погрешности измерения профиля температур
Результаты моделирования позволяют
установить для данного случая оптимальное
значение р= 4, при котором МО абсолютной
погрешности измерения профиля температуры после
коррекции снижается до значения ![]() = 0,0533 оС. Сравнивая
значения
= 0,0533 оС. Сравнивая
значения ![]() при оптимальном
значении р=4 с аналогичным результатом в [1] для
линейного закона изменения статической
составляющей погрешности по глубине (
при оптимальном
значении р=4 с аналогичным результатом в [1] для
линейного закона изменения статической
составляющей погрешности по глубине (![]() =0,1888 оС), установим
коэффициент эффективности предложенного метода:
=0,1888 оС), установим
коэффициент эффективности предложенного метода:
КЭФ1=![]() /
/![]() = 3,54.
= 3,54.
Учитывая, что оптимальное значение р
зависит от разницы постоянных времени каждого из
каналов измерения температуры градиентомера,
проведены аналогичные исследования при 10%, 15% и 25%
отклонениях постоянных времени датчиков от
номинальных значений. В табл. 1 приведены
результаты расчетов оптимальных значений р,
оценок МО абсолютных погрешностей измерения
профиля температуры после коррекций по методу,
изложенному в [1] ![]() ,
предложенному в данной работе
,
предложенному в данной работе ![]() и коэффициентов эффективности КЭФ1
и коэффициентов эффективности КЭФ1
Таблица 1– Результаты исследований
эффективности предложенного метода коррекции по
статической составляющей погрешности при
различных отклонениях D t
/t СР.
(t 2-t 1)/t СР, % |
Оптимальн. Значение р |
Кэф1 |
||
10 |
600 |
517 |
1521 |
2,93 |
15 |
18 |
493 |
1589 |
3,39 |
20 |
4,0 |
533 |
1888 |
3,55 |
25 |
3,1 |
609 |
2074 |
3,41 |
Эффективности предложенного метода
при 10-25% рассогласовании постоянных времени
измерительных каналов температуры
градиентомера составляют 3…3,5 и имеют тенденцию
к незначительному увеличению с ростом
рассогласования постоянных времени . При этом
также незначительно увеличиваются значения
абсолютной погрешности![]() .
.
Коррекция динамической составляющей
погрешности измерения температуры выполнялась
по методике , изложенной в [1]. При этом с учетом
суммарногодействия коррекций по статической и
динамической составляющим для получения
минимальных погрешностей рассчитывались новые
значения оптимальных показателей степени р. В
табл. 2 приведены результаты исследований для
предложенного метода коррекции значений
абсолютных погрешностей ![]() при
тех же отклонениях D t/
t СР, аналогичные
данные по методу, изложенному в [1]
при
тех же отклонениях D t/
t СР, аналогичные
данные по методу, изложенному в [1] ![]() и коэффициенты эффективности нового
метода коррекции К эф2.
и коэффициенты эффективности нового
метода коррекции К эф2.
Таблица 2 – Результаты исследований
эффективности предложенного метода коррекции по
статической и динамической составляющим при
различных отклонениях D t
/t СР.
(t 2-t 1)/t СР, % |
Оптимальн. Значение р |
Кэф1 |
||
10 |
3 |
423 |
599 |
1,42 |
15 |
3,1 |
504 |
785 |
1,56 |
20 |
3,4 |
591 |
1031 |
1.74 |
25 |
3,5 |
661 |
1277 |
1,93 |
Эффективность предложенного метода
после коррекций статической и динамической
составляющих составляет 1,4…1,9 и также имеет
тенденцию к возрастанию при увеличении
рассогласования постоянных времени. Для этого
случая оптимальные значения параметра р
незначительно изменяются (3…3,5) при отклонениях D t /t СР в тех же пределах.
Учитывая, что в области минимума функции
погрешности ее значения несущественно
изменяются при изменении параметра р на ± 25% (см. рис. 1), можно рекомендовать
применять значение р= 3,25 без предварительной
оценки постоянных времени измерительных каналов
температуры. Для сравнения на рис. 2 представлены
наряду с истинным профилем температуры,
скорректированные двумя рассмотренными
методами и измеренные каналами градиентомера
профили температуры.
Здесь: 1– истинный профиль температуры
по теоретической модели; 2,3– профили, полученные
с учетом постоянных времени первого и второго
измерительных каналов температуры
градиентомера соответственно; 4–
скорректированный по базовому
градиентометрическому методу профиль
температуры; профили температуры после
компенсации статической и динамической
составляющих погрешности по методу, изложенному
в [1] – 5, и предложенному в данной работе – 6.

Рисунок 2– Профили температуры
Как следует из результатов
исследований, предложенный метод, в основу
которого положена гипотеза о степенной
зависимости статической составляющей ошибки по
глубине с определением оптимального значения
показателя степени р, более эффективен, чем
усовершенствованный градиентометрический метод
измерения профилей температур. Он позволяет
уменьшить абсолютную погрешность измерения
температуры как минимум в 1,5-2 раза при постоянном
оптимальном значении параметра р= 3,25 для
реальных значений рассогласования постоянных
времени измерительных каналов температуры
градиентомера D t
/t СР в пределах 10–25%.
Выводы
Литература
2000 г.
[ Главная страница ] [ Mагистeрская работа ] [
Избраные ссылки ]
Рекомендуемое разрешение
экрана 800x600
Последнее обновление - 11.04.2000
Разработчик: Ефименко Е. И.