УДК 621.316.935-52
ВЛИЯНИЕ НА РАБОТУ ФАЗОВОГО РЕГУЛЯТОРА
АКТИВНОЙ И ЕМКОСТНОЙ НЕСИММЕТРИИ СЕТИ
Кобазев В.П., Кошин Б.А., Бакуновская Н.В.
Донецкий государственный технический университет, кафедра ЭСИС
r504a@fcita.dn.ua
The influence of cable network capacity and active asymmetry on the phase controller work is estimated. The relation for the determination of relative capacity and active asymmetry are developed.
При автоматической компенсации емкостного тока замыкания на землю чаще всего используются регуляторы, основанные на фазовом принципе. Область применения таких регуляторов ограничена величиной естественной несимметрии сети [1].
Для описания электрической сети с изолированной нейтралью примем за основу трехфазную схему замещения приведенную в[2]..
При составлении схемы замещения и математическом описании сети примем следующие допущения.
Ввиду относительно небольшой суммарной длины линий в схеме замещения они представляются сосредоточенными параметрами. Активные и индуктивные сопротивления линий не учитываются.
Междуфазные емкости не учитываются, так как они не оказывают влияния на установившиеся процессы в сети.
Напряжения питающей сети относительно симметричны земли, т.е. U
A = UB = UC и сдвиг фаз составляет 120 эл. град.Схема замещения сети приведена на рис.1.
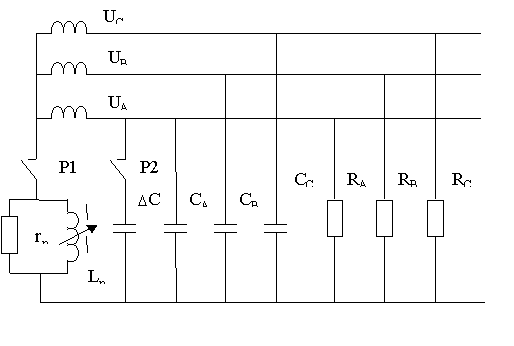
Рисунок – 1 Трехфазная схема замещения
С учетом допущений для трехфазной сети ( на схеме разъединители Р1 и Р2 отключены) напряжение
смещения нейтрали, в общем виде, определяется известным выражением:
![]()
где U
A, UB, UC, - фазные напряжения питающей сети. YA, YB, YC, - проводимости фаз сети относительно земли. Y - суммарная проводимость сети. При условии симметрии напряжения имеем:![]() . (1)
. (1)
С целью представления полученного выражения в относительных величинах введем следующие обозначения:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Подставляя эти величины в (1) получим следующее выражение:
![]() . (2)
. (2)
Учтем фазные множители симметричной трехфазной системы:
![]()
![]() .
.
Подставим множители в выражение (2) для 3U
o. После преобразования имеем: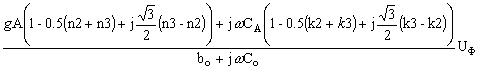
Представим комплексные числа в последнем выражении в показательной форме:
![]() , (3)
, (3)
где
![]() ;
;
![]() , (4)
, (4)
где
![]() ;
;
![]() ,
, ![]() .
.
Структура подкоренных выражений (3) и (4) одинакова, поэтому выполним преобразование одного из них, например (4). Для этого возведем во вторую степень подкоренные выражения:
![]() ,
,
![]() .
.
Объединим эти два выражения, и после проведения преобразований получим:
![]() .
.
Для выражения (3) по аналогии имеем:
![]() .
.
Таким образом, с учетом выполненных преобразований выражение (2) может быть записано в следующем виде:
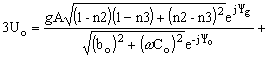
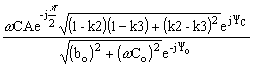
Представим эти выражения в виде двух составляющих:
![]() ,
,
где Uнс
R - составляющая, обусловленная несимметрией активных проводимостей изоляции сети относительно UнсС - составляющая, вызванная несимметрией емкостей фаз относительно земли.Первая составляющая определяется по соотношению:
![]() ,
,
где
Вторая составляющая вычисляется по выражению:
![]() ,
,
где
Рассмотрим отношение составляющих напряжения нейтрали:
![]() , (5)
, (5)
где dи - коэффициент успокоения сети с изолированной нейтралью.
Результаты расчета несимметрии по (5) для dи = 0.06 при изменении ко от 0.001 до 0.03 с шагом 0.05 и по n
o от 0.2 до 1, приведены на рис.2.
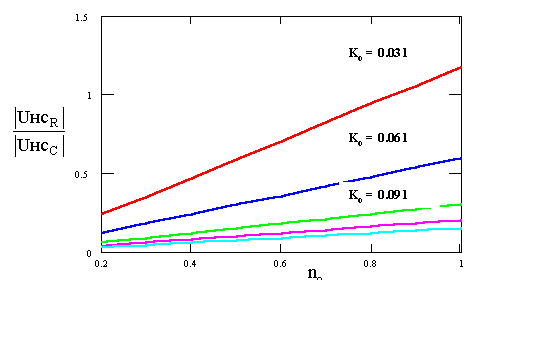
Рисунок 2 – Характеристики несимметрии сети
Из результатов расчета следует, что чем больше емкостная несимметрия тем меньше влияние несимметрии активных проводимостей. В кабельных электрических сетях при ко < 0.001 напряжение несимметрии определяется несимметрией активных проводимостей, питающих напряжений, т.е. по существу случайными факторами. Поэтому при неизменной конфигурации сети напряжение несимметрии в кабельной сети менее стабильно, чем в воздушной линии, хотя по величине оно и не велико. Таким образом, при включении дополнительного конденсатора D С между фазой сети и землей будет практически полностью подавляться естественная несимметрия в кабельных сетях. Следовательно для математического моделирования фазового регулятора необходимо учитывать только несимметрию создаваемую конденсатором D С.
Для сети с компенсацией емкостного тока и при отсутствии несимметрии активных проводимостей относительно земли выражение, описывающее напряжение смещения нейтрали имеет вид:
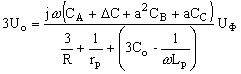 .
.
Учитывая, что
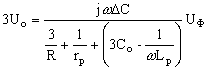 .
.
Разделим числитель и знаменатель на
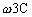 и учтем, что
и учтем, что
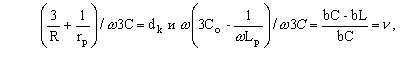
где d
k – коэффициент успокоения компенсированной сети,n
- степень расстройки дугогосящего реактора (ДР)тогда это выражение для 3U
o представим в следующем виде:![]() . (6)
. (6)
Комплексное выражение (6) это амплитудно-фазовая характеристика сети, описываемая следующими соотношениями:
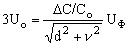
![]()
Фаза напряжения дана относительно тока, ID
C конденсатора D С в зависимости от степени расстройки. Так как сопротивление конденсатора во много раз больше суммарного сопротивления контура нулевой последовательности, то положение вектора ID C при расстройке ДР практически неизменно, а вектор напряжения смещения нейтрали 3Uo перемещается.При резонасной настройке ДР (n = 0) сопротивление контура нулевой последовательности становится активным. При этом напряжение 3U
o совпадает по направлению с током ID C При включении конденсатора D С между фазой А сети и землей векторы тока ID C и линейного напряжения UCB совпадают. В связи с этим на практике угол j измеряют между напряжениями 3Uo и UCB. В данном случае напряжение UCB является опорным.При емкостном сопротивлении сети 3w
Co меньшем индуктивного сопротивление реактора 1/w Lp сопротивление контура нулевой последовательности имеет емкостной характер. Поэтому вектор 3Uo отстает от вектора тока ID C, а расстройка ДР характеризуется недокомпенсацией (n >0).Если 3w
Co >1/w L сеть переходит в режим перекомпенсации (n <0), что вызывает изменение взаимного расположения векторов 3Uo и ID C. В этом случае вектор тока ID C опережает вектор 3Uo.В процессе эксплуатации емкость сети изменяется и соответственно изменяется соотношение емкостей конденсатора D С и сети Со При резонансной настройке дугогасящего реактора будет максимальное напряжение
смещения нейтрали 3Uo. В соответствии с правилами технической эксплуатации сети величина 3Uo не должна превышать 0.15 UФ. Поэтому емкость конденсатора D С можно выбрать из условия:![]()
где 3U
oрез – напряжение смещения нейтрали при резонансной настройке ДР,U
Ф – фазное напряжение сети;Соmin – минимальная емкость сети относительно земли.
Так как необходимая чувствительность измерительного органа регулятора обеспечивается при
![]()
ВЫВОДЫ
Получены соотношения для определения относительной, активной и емкостной несимметрии кабельной сети.
Из результатов расчета следует, что при моделировании работы регулятора, нужно учитывать только емкостную несимметрию кабельной сети.
Несимметрия необходимая для работы регулятора может создаваться искусственно, емкостью конденсатора, включенного между фазой сети и землей. При этом, естественная несимметрия кабельной сети не оказывает существенного влияния на работоспособность фазового регулятора.
ЛИТЕРАТУРА
1. Сирота И.М., Кисленко С.Н., Михайлов А.Н. Режимы нейтрали электрических сетей. - К. Наук. Думка, 1985г. - 264с.
2. Ершов А.М., Петров О.А. Амплитудно-фазовые характеристики компенсированной сети // Энергетика Известия вузов. - 1980, №5 с. 23-27