МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В СИСТЕМЕ ЭЛЕКТРОСНАБЖЕНИЯ СОБСТВЕННЫХ НУЖД ЭЛЕКТРОСТАНЦИЙ ПРИ ОТКЛОНЕНИЯХ НАПРЯЖЕНИЯ И ЧАСТОТЫ
Талал Ал Ас
Донецкий государственный технический университет
Главной особенностью систем электроснабжения собственных нужд (с.н.) электростанций является применение трансформаторов рабочего и резервного питания с расщепленной обмоткой низшего напряжения, а также применение асинхронных двигателей (АД) большой единичной мощности (200-8000 кВт), короткозамкнутый ротор которых выполняется глубокопазным с целью улучшения пусковых и рабочих характеристик за счет использования эффекта вытеснения тока.
Для анализа стационарных и переходных процессов в системах с.н. требуется разработка математических моделей как их отдельных элементов (трансформаторов, асинхронных двигателей, шинопроводов и др.), так и системы в целом. Особенно это актуально для прогноза сбалансированного деления узлов нагрузки при глубоких снижениях частоты. Этим вопросам посвящены работы [1,3,5]. К основным недостаткам этих работ относятся возможность применения разработанных моделей для анализа только стационарных [1,5] или только переходных [3] процессов. Приближенный учет эффектов вытеснения тока и насыщения магнитных цепей с помощью импирических зависимостей [1,5] вызывает в ряде случаев несоответствие расчетов реальным физическим процессам или несоответствие расчетных данных в синтезированной схеме каталожным [2]. Кроме того, в [2-5] отсутствует возможность выполнения расчетов потребляемой мощности и ее потерь, токов статора, ротора и других параметров двигателей и системы с.н. для важных эксплуатационных режимов, которые сопровождаются отклонением частоты и величины напряжения и др.
В данной работе предлагается математическая модель системы электроснабжения с.н
. не имеющая указанных недостатков, что достигнуто за счет более корректного учета указанных выше явлении вытеснения тока и насыщения магнитной системы асинхронного двигателя, а также учета потерь и явлений взаимоиндукции между расщепленными обмотками трансформатора. Модель позволяет выполнить анализ
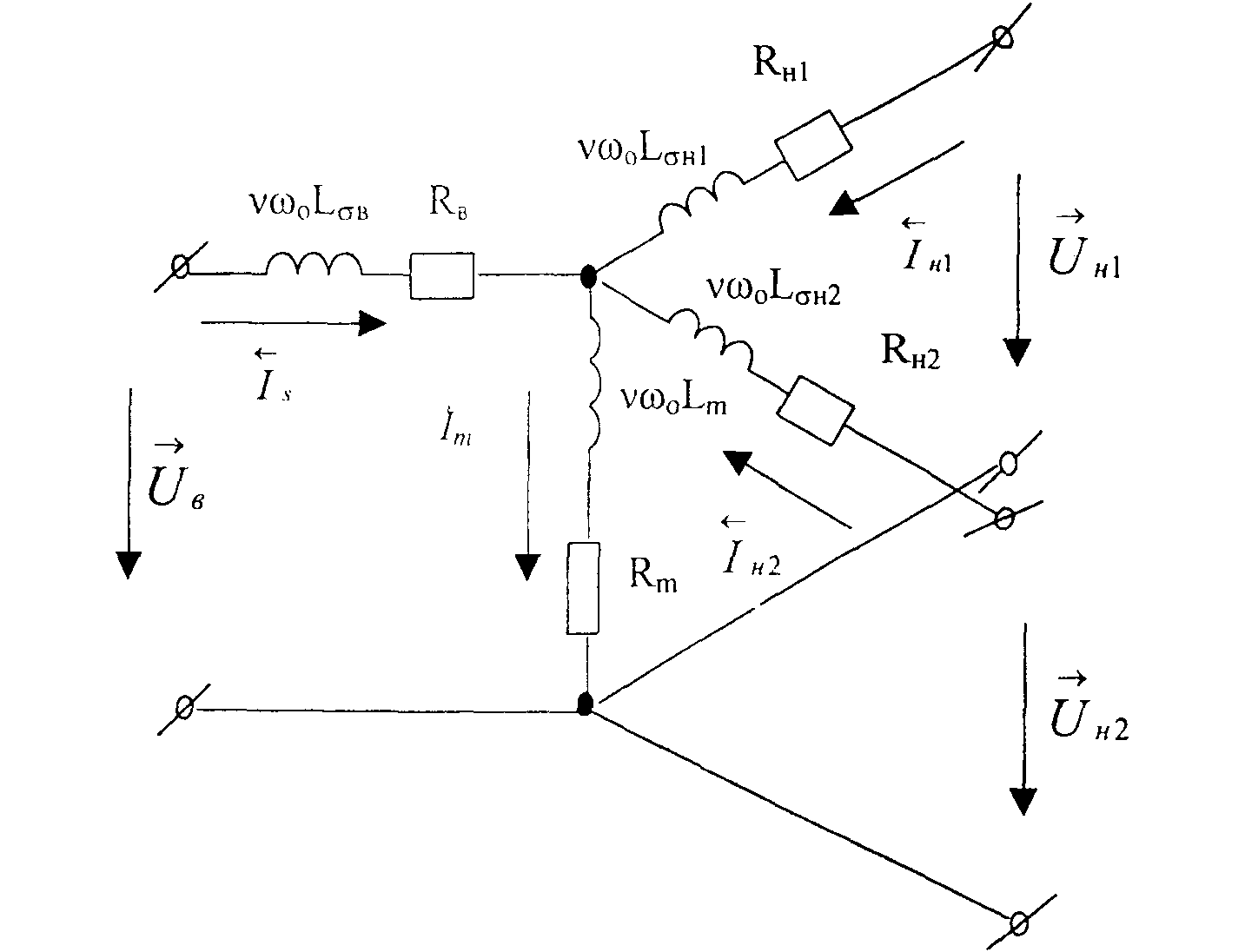
Рисунок 1- Эквивалентная схема замещения трансформатора с расщепленной обмоткой
процессов в системе с.н. для различных напряжений и частоты.
Для типовой схемы электроснабжения с.н. ТЭС математическая модель представлена уравнениями
рабочего и резервного трансформаторов, асинхронных двигателей с.н., шинных или кабельных магистралей резервного питания с.н.Расчетная схема замещения трансформатора с расщепленной обмоткой, приведенная к одной ступени напряжения, показана на рисунке 1.
Уравнения равновесия э.д.с. для контуров, образованных обмотками высшего и низшего напряжения
трансформатора, имеют вид.
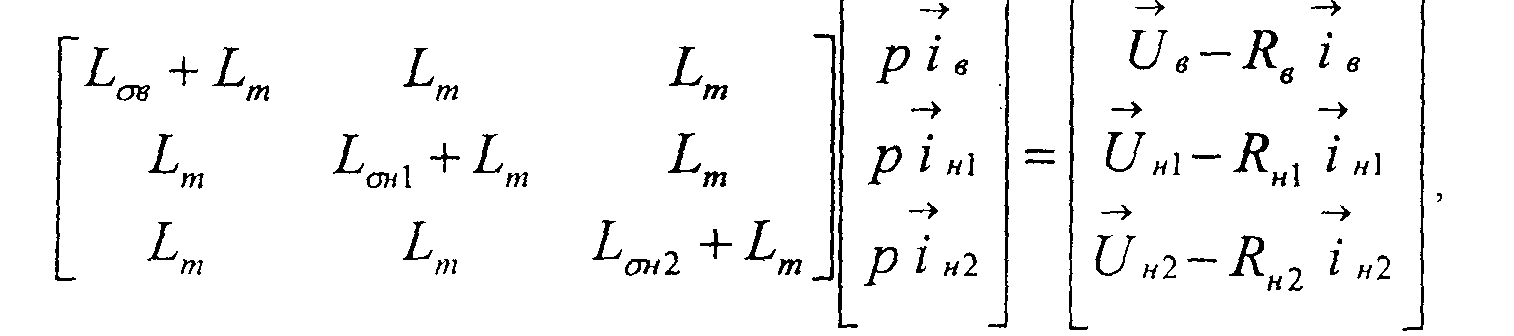
где р =
d/dt для переходных режимов и р =jw - для стационарных режимов.Параметры схемы (рис. I), определяем, используя каталожные данные и данные опытов короткого замыкания и холостого хода (хх) трансформатора:
Схему замещения глубокопазного асинхронного двигателя (рис. 2) примем с учетом явления вытеснения тока в роторе путем представления последнего двумя эквивалентными контурами, с учетом насыщения главного магнитного потока, представив индуктивность ветви намагничивания, на основе характеристики хх машины, как нелинейную функцию от тока намагничивания, а насыщение магнитных потоков рассеяния всей машины с помощью нелинейной индуктивности обмотки статора, являющейся функцией тока статора.
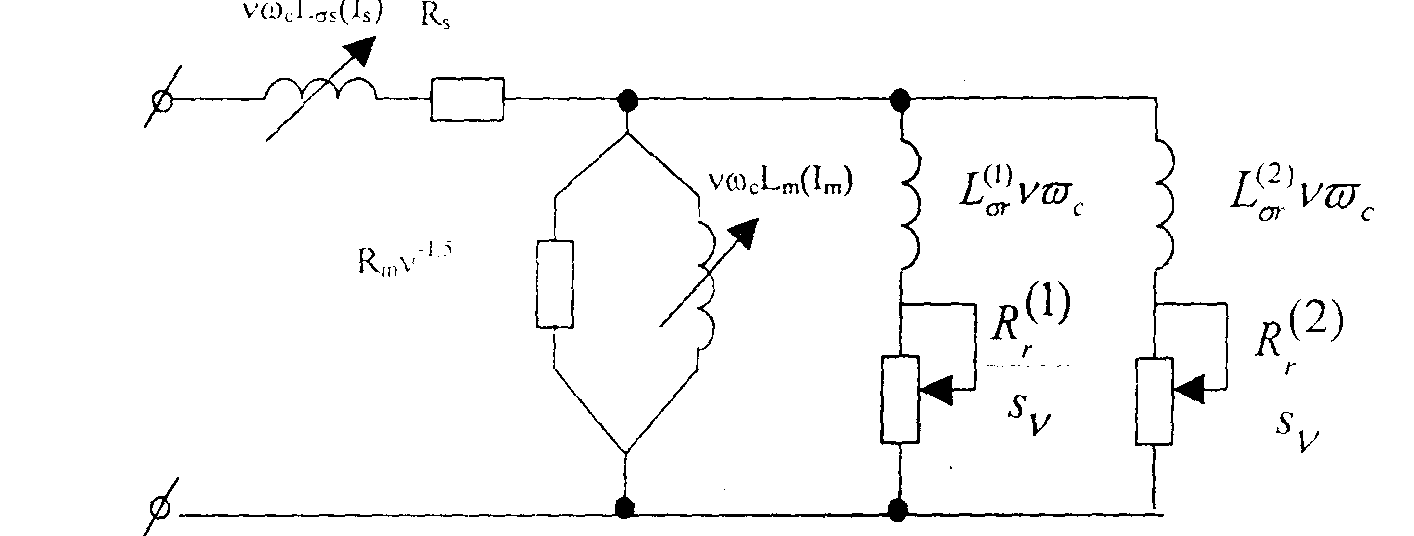
Рисунок 2 - Эквивалентная схема замещения глубокопазной асинхронной машины для
cmaционарных режимов,в которой учтены явления вытеснения тока в роторе и насыщение
магнитных цепейПри синтезе параметров указанной схемы замещения будем исходить из известных каталожных данных двигателя, из типовой характеристики хх двигателей с.н. и зависимости сопротивления рассеяния статора от тока, приведенной в [3] и полученной на основе расчетно-экспериментальных исследований. Эта зависимость
L
σ(i) может быть представлена, как![]()
где
I s - ток статора в отн. ед.; K0= 0,6 - 0,9 начальное значение коэффициента насыщения при пусковомтоке статора с заторможеным ротором и Us=Uном; Lσsном -значение индуктивности рассеяния при
номинальном токе статора.
Влияние частоты питающего напряжения учтено в схеме замещения (рис. 2) с помощью коэффициента
V
ω0, на который умножаются соответствующие индуктивности. При этом ω0 =314,15с-1 ,что соответствует номинальной частоте f0 =50 Гц, а v - это отношение текущей частоты f к номинальной f0 .Как известно [4], отклонение частоты питающего напряжения от номинальной влияет на потери в стали,
что в схеме замещения (рис. 2) учтено умножением сопротивления
Rm, соответствующего частоте f0 , на коэффициент v в степени -1,5Зависимость индуктивности ветви намагничивания от тока намагничивания на основе характеристики хх [3] была нами получена с использованием ее аппроксимации отношением двух полиномов. Ниже она приведена в виде аналитической зависимости, справедливой для всех двигателей
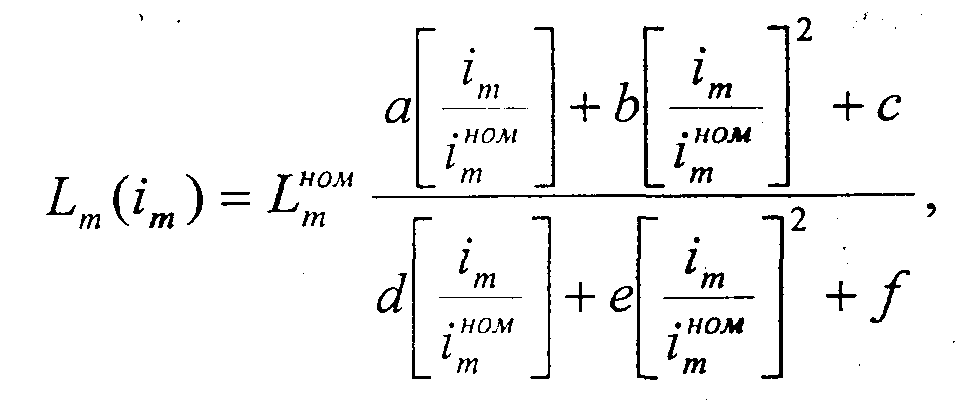
где Lmном - значение индуктивности ветви намагничивания при номинальном токе намагничивания
Im
ном ,имеющем место при номинальном напряжении статора и холостом ходе двигателя, а = 58379; b = -183,7; с = 0,00275; d = 347,7; e = 1,034; f= 51,966.Для синтеза схемы замещения составим минимизируемую функцию цели, равную сумме квадратов отклонений вращающих моментов двигателя, рассчитанных по схеме замещения, и каталожных для скольжений Sном, Sкр и 1, токов статора для Sном и 1, к.п.д. двигателя расчетного и каталожного при Sном . Ниже приведен фрагмент MathCad-документа, с помощью которого осуществлялся синтез параметров эквивалентных схем замещения асинхронного двигателя.
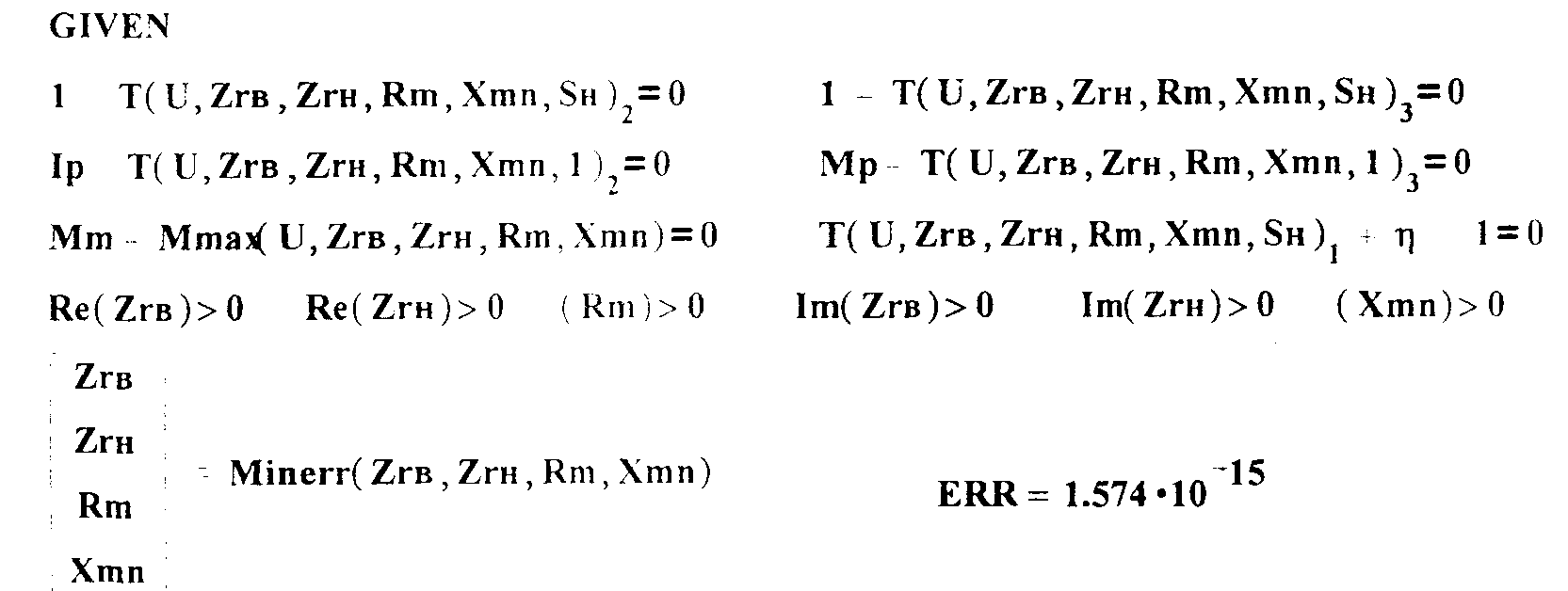
В качестве примера приведем значения в отн.ед. найденных по каталожным данным по изложенной методике параметров схем замещения для трансформатора с.н. типа ТРДНС 40000/110:
Rs=0.002124; Xσв= -,045;R
н1= Rн2=0,004247; Xσн1= Хσν2=0.15; Rm=28,072; Xm=179,68, а также для асинхронного двигателя типа ВДД 213/54-16 мощностью 1700 кВт: Zs=0,0054 + j0,093; Zr(1)=0,152 + J0.142; Zr(2) =0,0065 – j0.162; Rm=21;Xm
ном=2,225. При проверке пусковых токов и моментов, найденных по схеме замещения, они совпали с исходными каталожными с высокой точностью (расхождение менее 0,01 процента). Зависимости от скольжения тока статора и вращающего момента для различных напряжений при f= const приведены на рисунке 3, а для различных частот при U = const - на рисунке 4. Как видно из рисунков при понижении напряжения или при повышении частоты вращающий момент и ток статора АД снижаются.Функциональные зависимости критического момента и критического скольжения от величины питающего напряжения (таблица 1) и разных значений частоты (таблица 2) позволяют выявить влияние вытеснения тока и насыщения на эти величины.
Таблица I-Данные максимального момента и критического скольжения АД типа ВДД 21 3/54-
|
Показатель |
Кратность напряжения по отношению к номинальному |
||||
|
0,9 |
0,95 |
1,0 |
1,05 |
1,1 |
|
|
Ммакс |
2,027 |
2,27 |
2,5 |
2,76 |
3,02 |
|
skp,% |
2,586 |
2,588 |
2,59 |
2,6 |
2,623 |
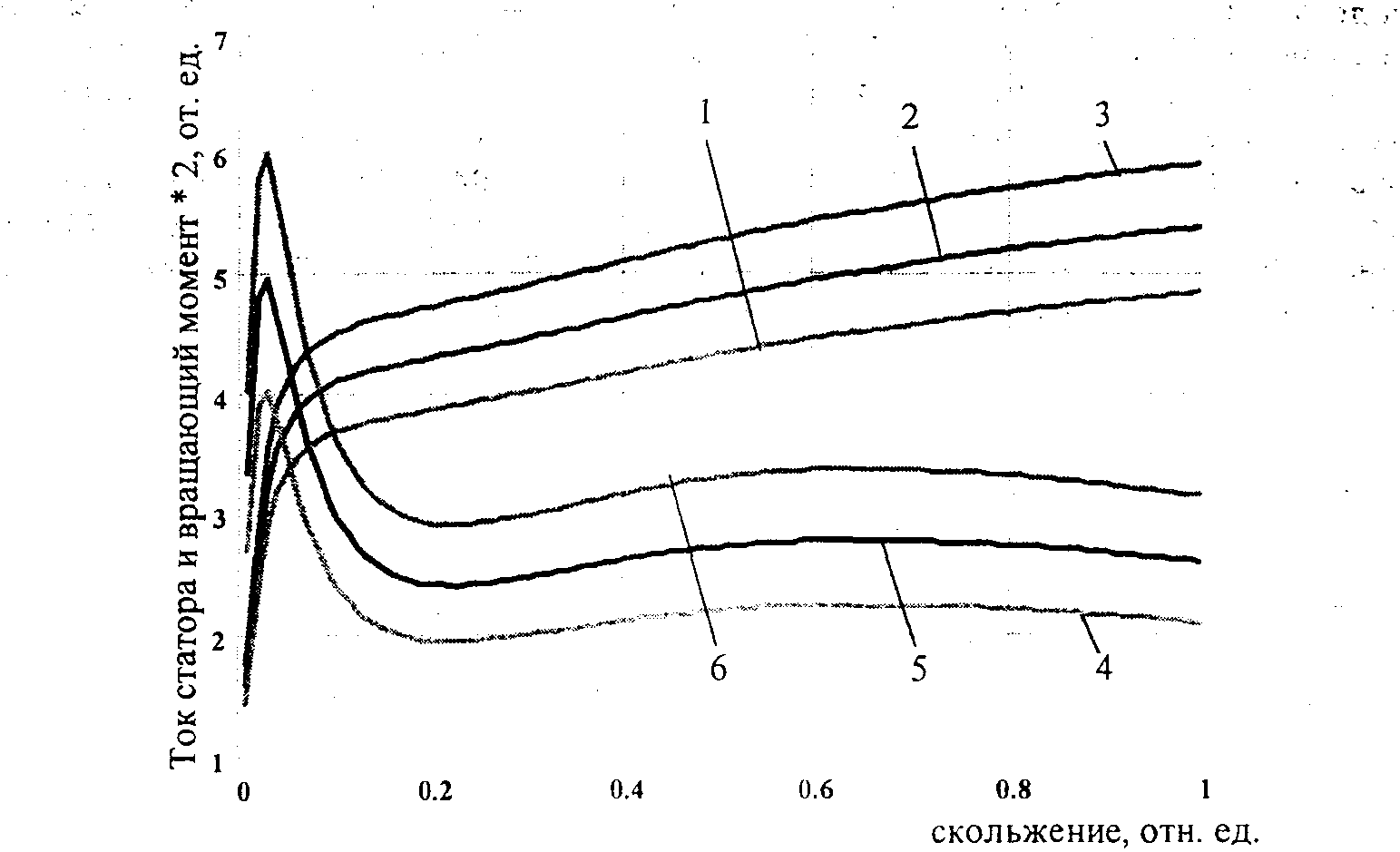
Рисунок 3 — Пусковые характеристики тока статора (/,2,3) и вращающего момента (4,5,6) асинхронного двигате.-м типа ВДЦ213/54-16 при напряжениях соответственно равных 0,9, I и 1,1 от номинального
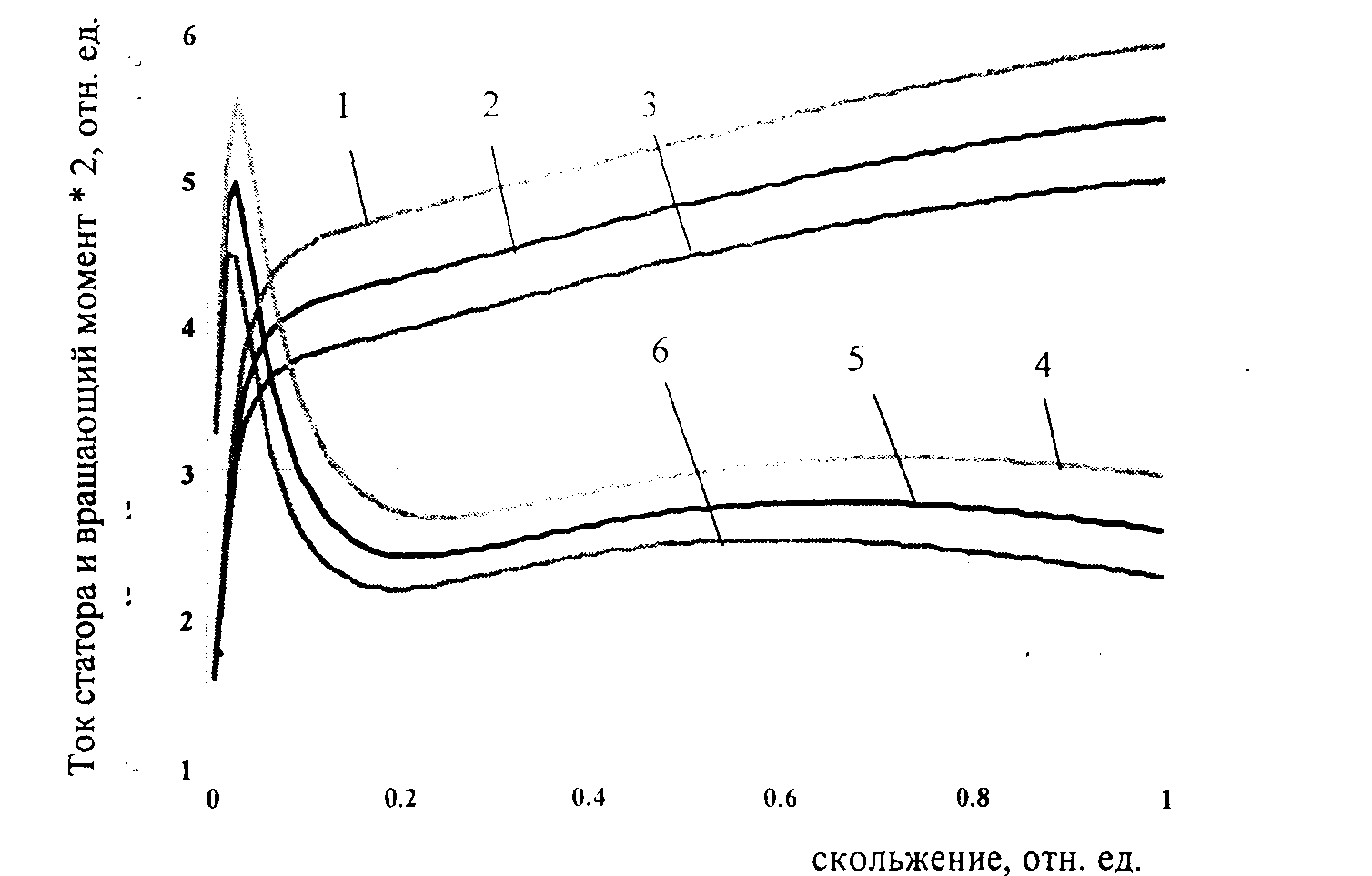
Рисунок 4 - Пусковые характеристики тока статора (1,2,3) и вращающего момента (4,5,6) асинхронного двигателя типа ВДД 213/54-16 при частотах
сети соответственно равных 0,9, J и 1,1 от номинальнойТаблица 2- Данные максимального момента и критического скольжения АД типа ВДД 213/54-16
при изменении частоты
питания|
Показатель |
Кратность частоты |
||||
|
0,9 |
0,95 |
1,0 |
1,05 |
1,1 |
|
|
Ммакс |
2,768 |
2,627 |
2,5 |
2,38 |
2,28 |
|
sкр .% |
2,89 |
2,75 |
2,59 |
2,48 |
2,36 |
Разработанная модель позволяет оценить влияние на режимные параметры отклонений частоты, напряжения, а также влияние совместного их отклонения. Характер изменения тока статора, вращающего момента и суммарных потерь двигателя при изменении напряжения в диапазоне 0,9 - 1,1 номинального показан на рисунке 5, а при изменении частоты в таком же диапазоне - на рисунке 6. При моделировании момент сопротивления принимался пропорциональным коэффициенту загрузки и квадрату частоты вращения, что позволяет по значению вращающего момента дать оценку производительности механизма с вентиляторным моментом сопротивления. Для различных значений частоты и напряжения ток статора и другие режимные параметры могут быть найдены по графикам или таблицам, построенным по результатам расчета (рисунок 7).
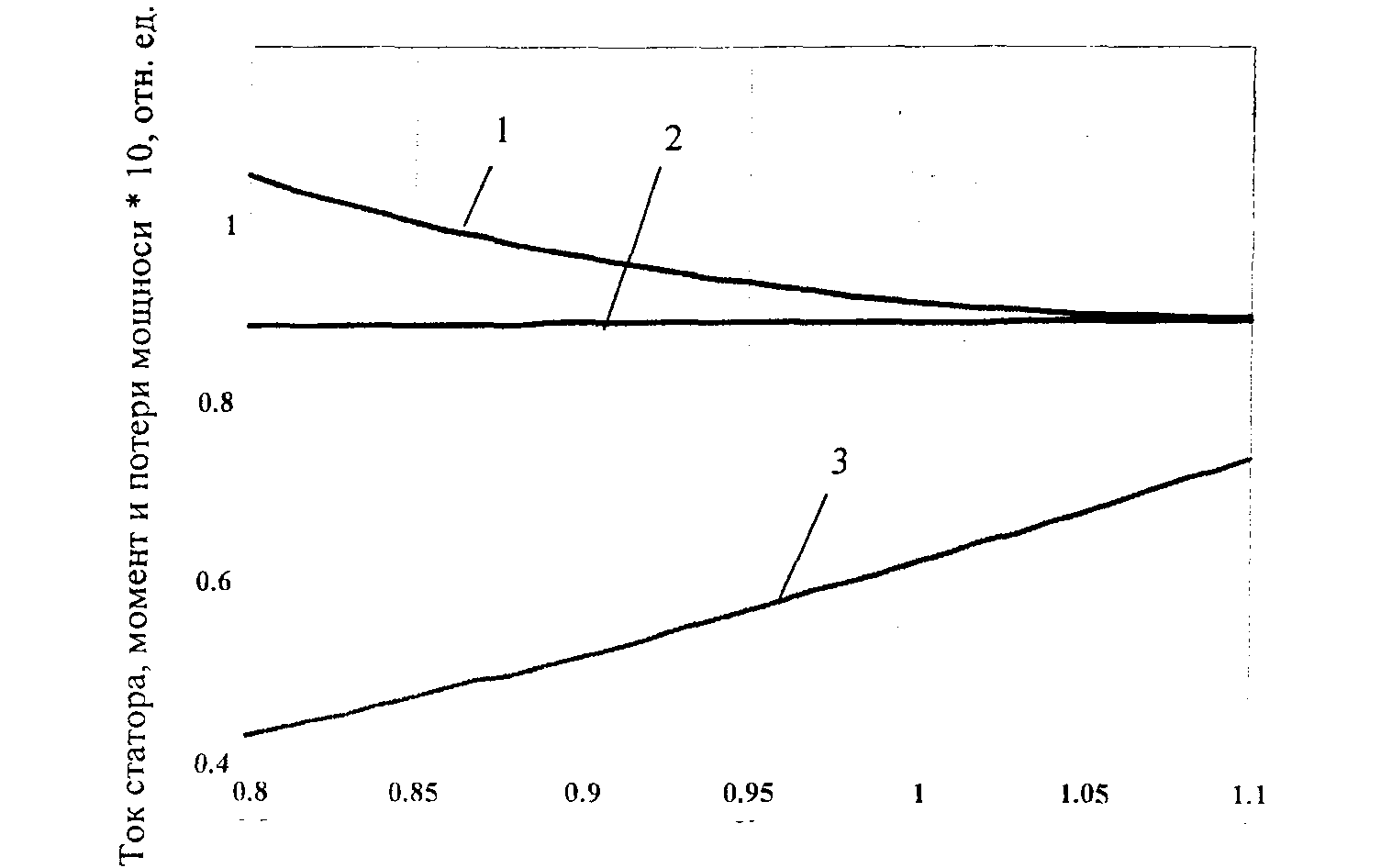
Рисунок 5 - Изменение тока статора (I), вращающего момента (2) и потерь мощности (3) асинхронного двигателя типа ВДД 213/54-16 при изменении напряжения
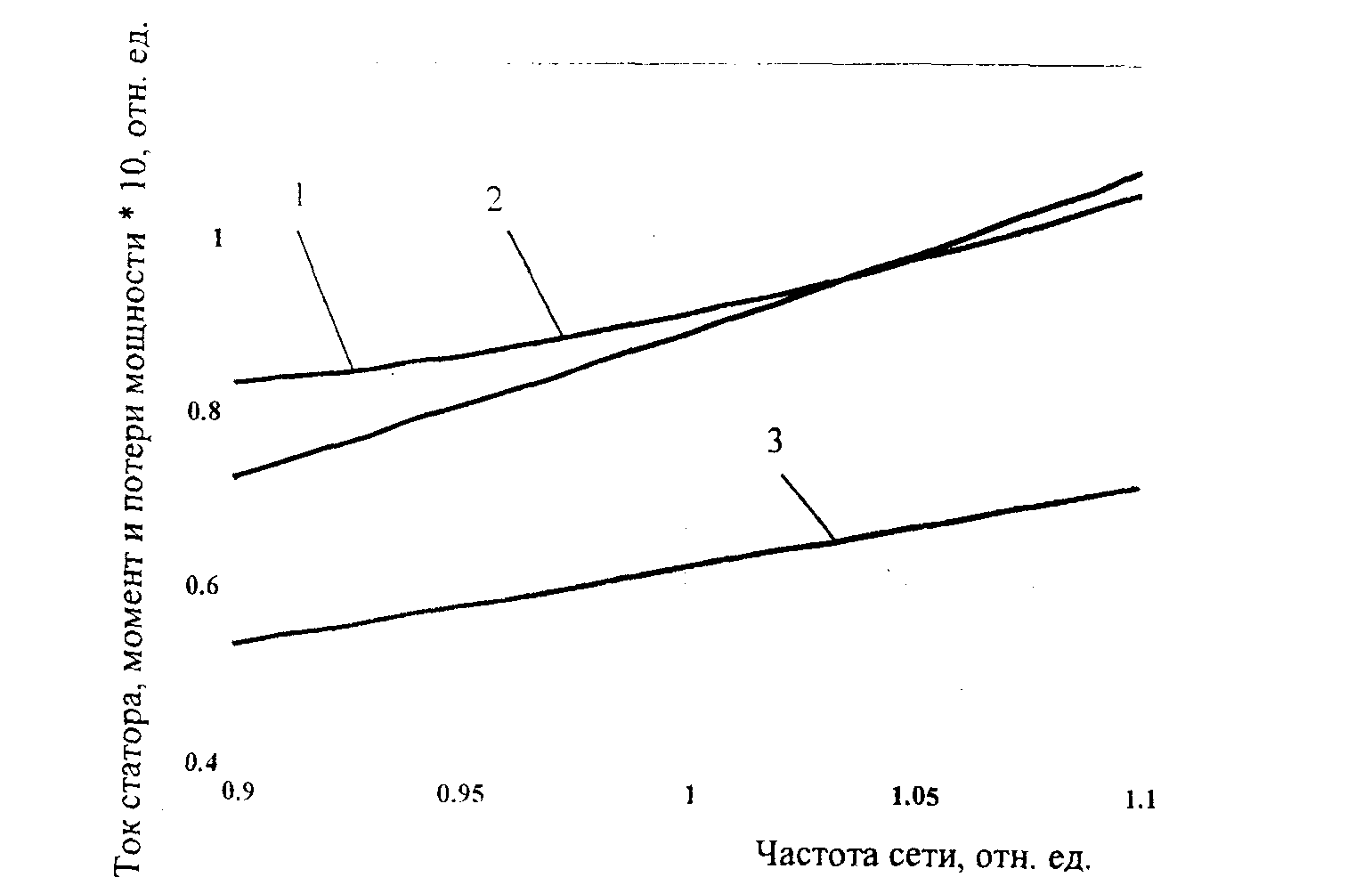
Рисунок 6 - Изменение тока статора (1), вращающего момента (2) и потерь мощности (3) асинхронного двигателя типа ВДД 213/54-16 при изменении частоты
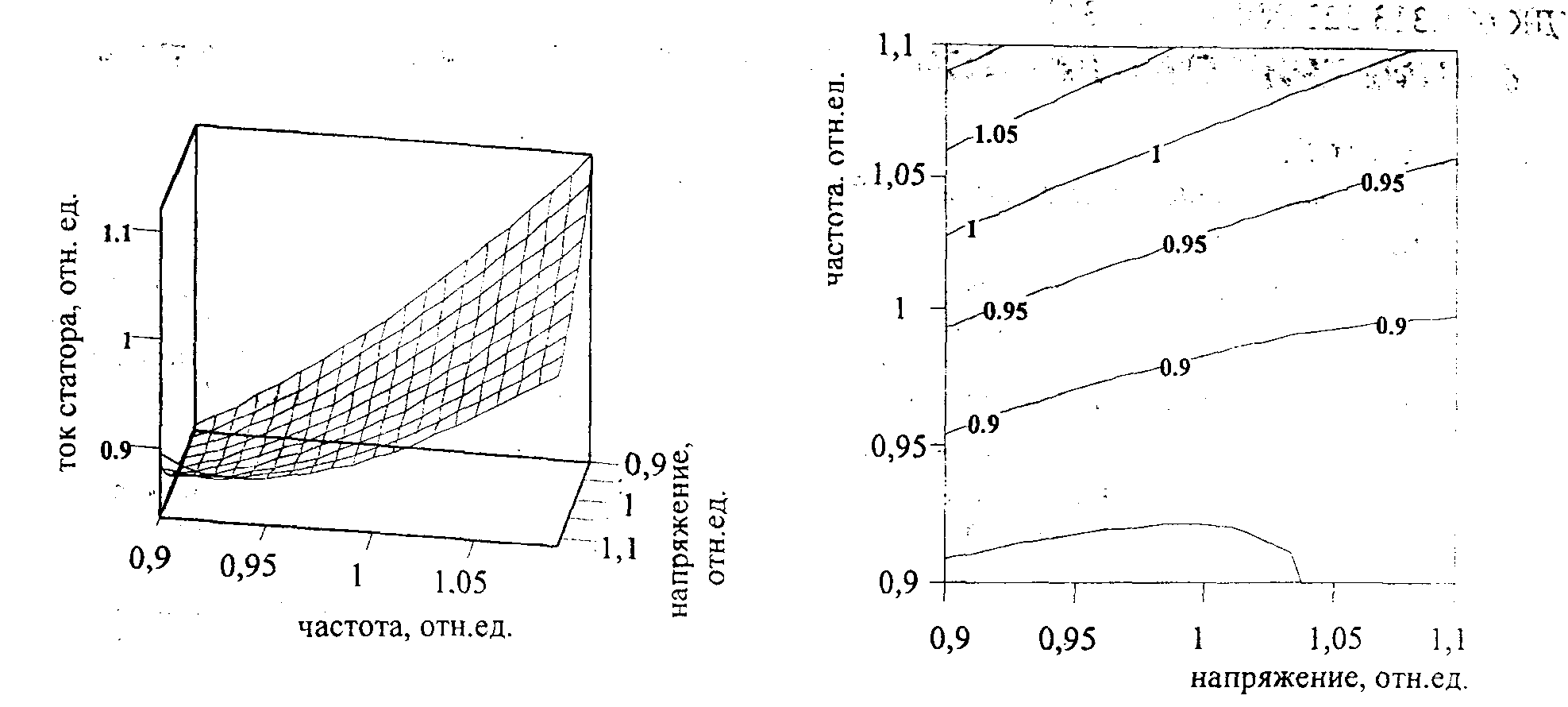
Рисунок 7 -Характер изменения тока статора в функции величин напряжения статора и частоты питающей сети
Приведенная математическая модель позволяют выполнить анализ режимов работы и потерь для анормальных значений напряжения и частоты как для отдельных элементов, так и для системы с.н. в целом. При моделировании с учетом большого количества двигателей на каждом шаге расчета сначала находим напряжение на сборных шинах, а затем из уравнений для отдельных элементов итерационным методом определяем значения их текущих параметров режима. Приведем результаты расчета потребляемой мощности, тока трансформатора и потерь мощности в системе с.н. блока 300 МВт при номинальном питающем напряжении 115 кВ для частот 50 и 47,5 Гц. Эти величины составили соответственно 26 и 23,9 МВт; 153,57 и 161,65 А; 6,2 и 5.8 °о. Oтклонение этих расчетных параметров от экспериментальных данных не превышает 2,2%.
ВЫВОДЫ
1. Разработана математическая модель системы электроснабжения с.н., позволяющая определить режимные параметры системы с.н. и отдельных ее элементов при отклонениях напряжения и частоты, в связи с чем представляется возможным прогнозировать поведение системы с.н. в рабочих и аварийных режимах.
2. Отличительной особенностью модели является учет вытеснения тока в роторе глубокопазных АД г потерь в стали с учетом насыщения и явления гистерезиса, а также насыщения потоков рассеяния. Предложен и реализован метод синтеза параметров АД по каталожным данным с учетом отмеченных явлений.
ЛИТНРАТУРА
1. Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей Под ред Л.Г.Мамиконянца. - М.: Энергоатомиздат, 1984. - 240 с..
2. Мощинский Ю.А., Беспалов В.Я., Кирякин А.А. Определение параметров схемы замещение асинхронной машины по каталожным данным. Электрнчесво, 1998, № 4, с. 38-42.
3. Сивокобыленко В.Ф., Костенко В.И. Математическое моделирование электродвигателей собственны' нужд электрических станций. Учебное пособие. Допецк, ДПИ, 1979- 111с.
4. Копылов И.П. Электрические машины: Учебник для вузов. - М.: Энергоатомиздат, 1986. - 360 с.
5.Баков Ю.В. Проектирование электрической части электростанций с применением ЭВМ: Учеб. nocooiiL для вузов - М.: Энергоатомиздат, 1991 - 272 с.