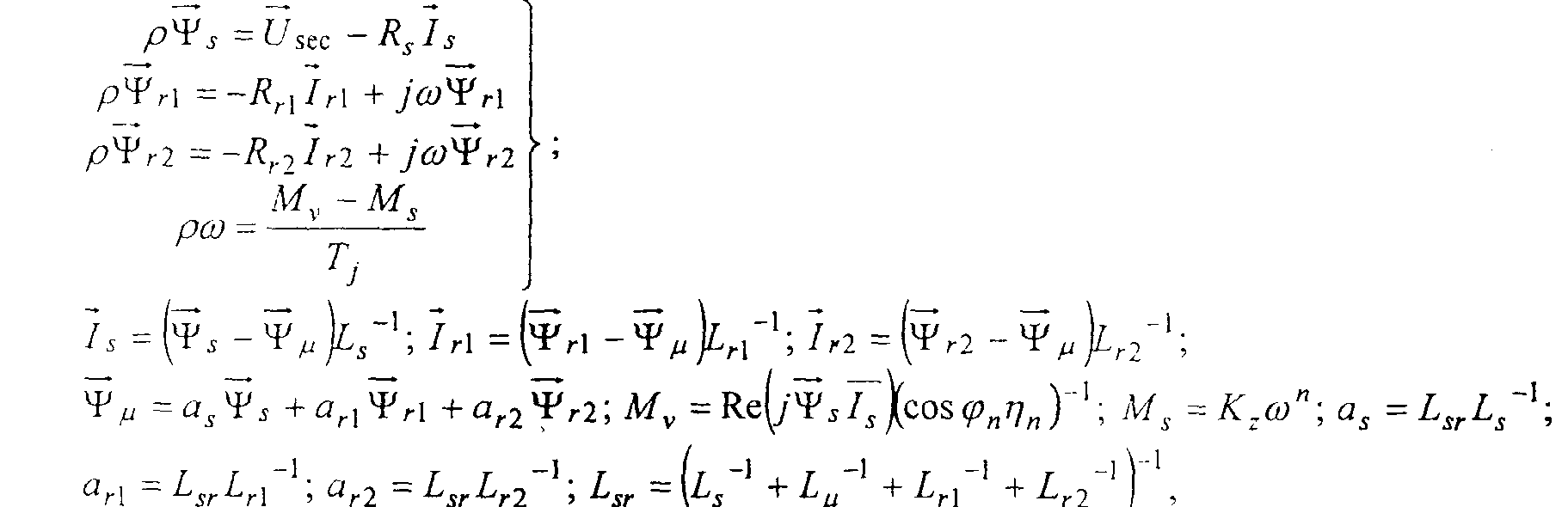
МЕТОД УЧЕТА ПОДПИТКИ МЕСТА КОРОТКОГО ЗАМЫКАНИЯ АСИХРОННЫМИ ДВИГАТЕЛЯМИ В СИСТЕМЕ СОБСТВЕННЫХ НУЖД
ЭЛЕКТРОСТАНЦИИСивокобыленко В. Ф., Павлюков В. А., Берепубо Э. Ф.
Донецкий государственный технический университет
В системе собственных нужд (с.н.) электрической станции основными потребителями являются глубокопазные асинхронные двигатели (АД). 6 - 0,4 кВ. Питание с.н. осуществляется от трансформаторов, подключаемых к выводам генераторов или к системам сборных шин (с.ш.) высокого напряжения. При коротких замыканиях (к.з.) двигатели посылают ток в точку к.з., значение которого соизмеримо с током от системы или генераторов. Таким образом, значение тока подпитки от двигателей во многом определяет тип выбранной коммутационной аппаратуры, сечения кабелей и другие параметры распределительных устройств. По этой причине методам расчета тока к.з. от двигателей уделяется большое внимание [1,2,3,4 и др.]. Однако, существующие методы или весьма приближенны и имеют большие погрешности [1] или достаточно сложны в реализации и требуют данные, которые отсутствуют в каталогах и информационных материалах заводов изготовителей [З].
С учетом изложенного, в данной работе на основе метода эквивалентирования [2] разработан способ расчета тока подпитки АД в системе с.н., отличающийся более высокой точностью по сравнению с [1] при использовании одинаковых с ним исходных данных. Это достигнуто за счет выявления и использования особенностей схем замещения глубокопазных АД, применяемых в системе с.н.
Рассмотрим сначала наиболее точный способ расчета тока к.з. в системе с.н., используя полные дифференциальные уравнения всех ее элементов.
Схема замещения типовой системы электроснабжения с.н. приведена на рис.1 и состоит из источника питания, двухобмоточного трансформатора, с.ш., асинхронных двигателей, статической нагрузки и шунта к.з. для моделирования удаленности места к.з.
Дифференциальные уравнения элементов расчетной схемы, записанные в неподвижной системе координат
:а
) для асинхпонного лвигателя: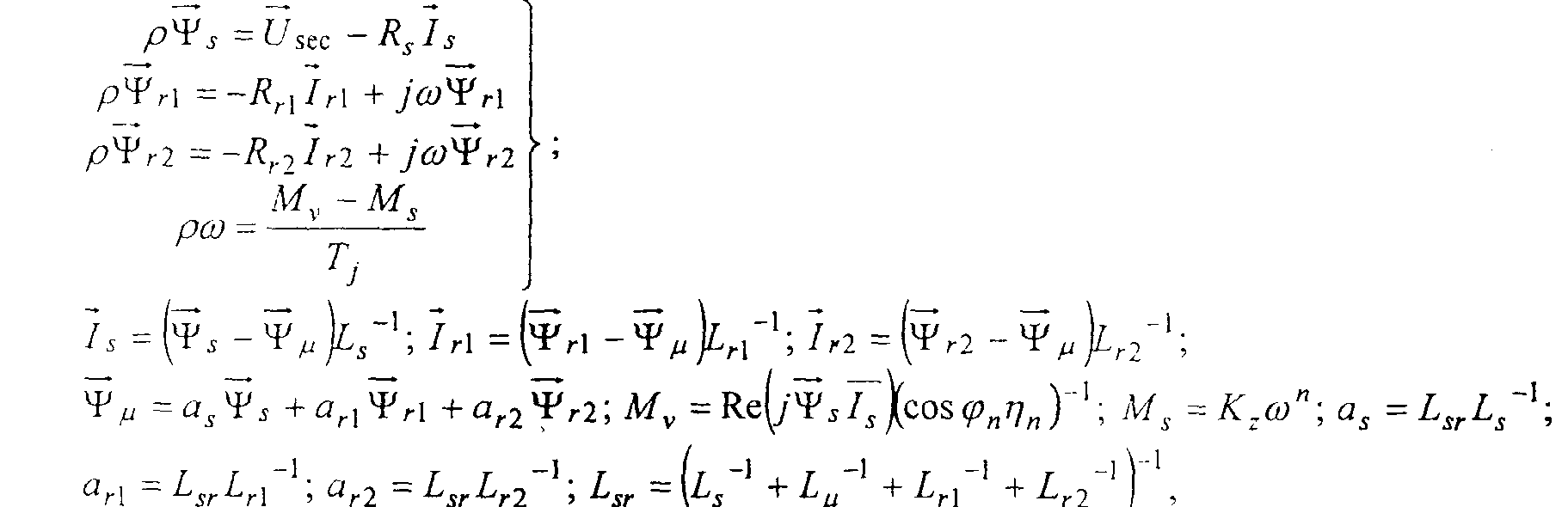
где:
Rs, Rr1, Rr2 и Lμ, Lσs, Lr1, Lr2 - активные сопротивления и индуктивности цепи намагничивания , рассеяния статора и контуров ротора эквивалентной схемы замещения глубокопазного АД, полученные по методике [2]; U sec- напряжение секции; Т.- механическая постоянная времени злектродвигательного агрегата с.н.;п -показатель степени, зависящий от типа механизма;
cosφn ,ηn- номинальные коэффициенты соответственно мощности и к.п.д. АД.б) для двухобмоточного трансфооматооа
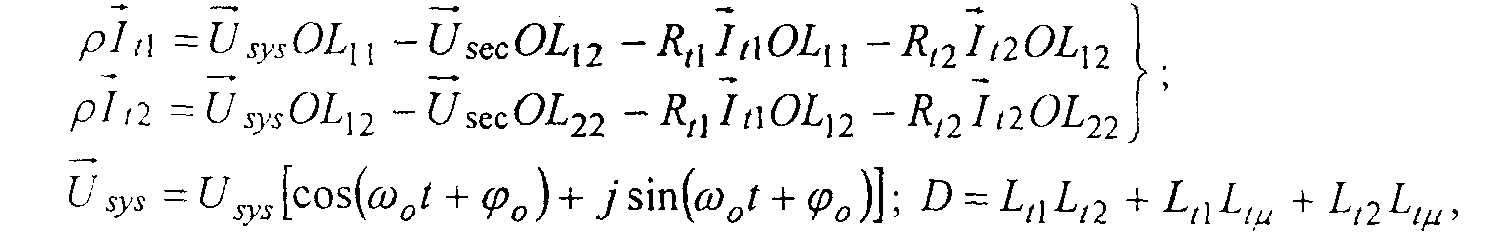
где:
OL11 =(L12+Ltμ)D-1 ; OL12 =LtμD-1 ; OL22 =(Lt1+Ltμ)D-1 - величины обратные индуктивностям трансформатора; Rt1,Rt2 и L1μ,Lt1,Lt2 - активные сопротивления и индуктивности соответственно цепи намагничивания, первичной и вторичной обмотки трансформатора; Usys , φ0 - модуль и фаза включения напряжения системы; ω0 =314,15 с-1 - синхронная частота вращения.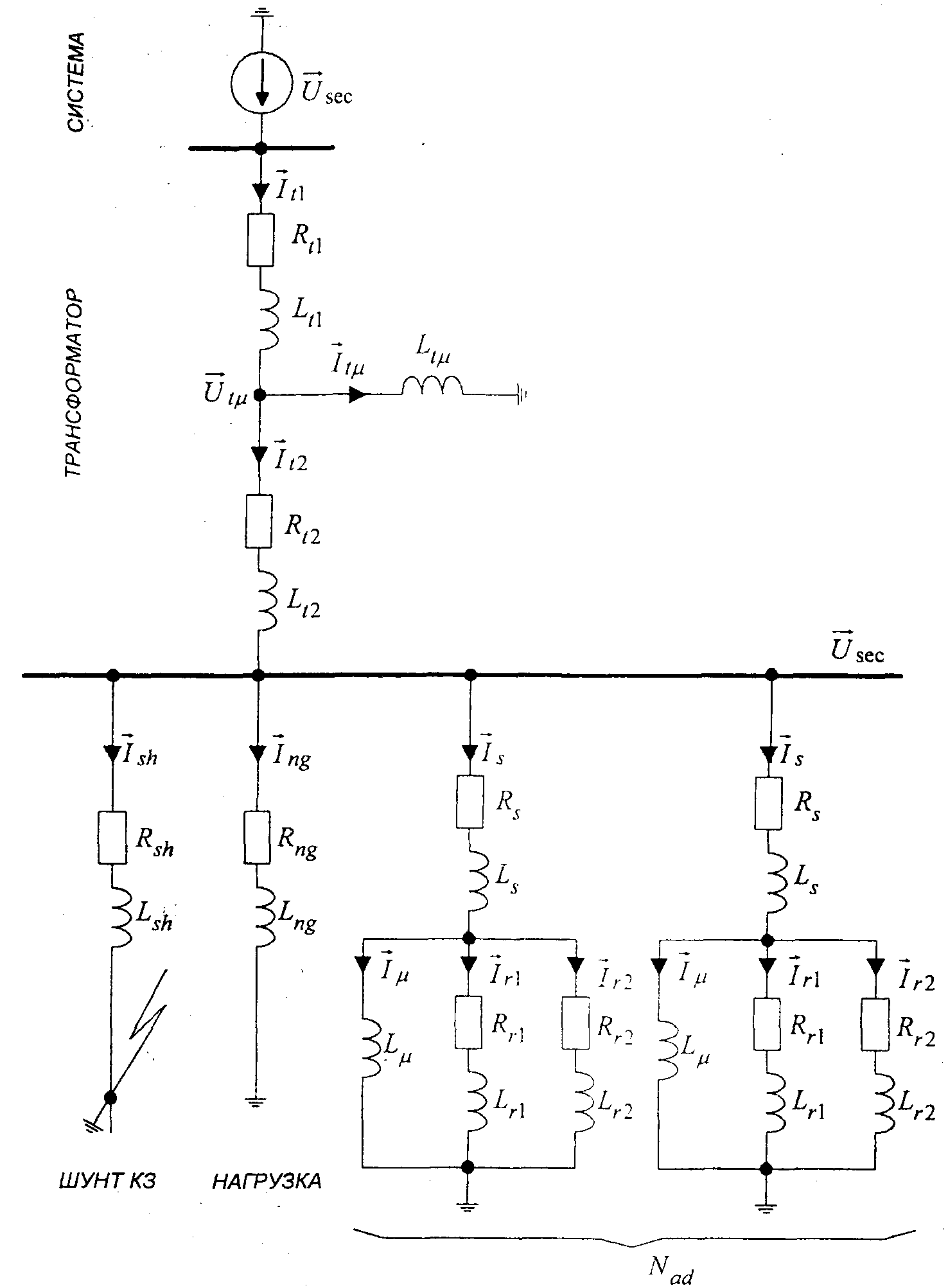
Рисунок 1 - Схема замещения системы электроснабжения собственных нужд в переходных режимах
Для решения дифференциальных уравнений элементов должно быть известно напряжение на шинах рабочего питания. Последнее на каждом шаге расчета находим по формуле, полученной в результате сложения выражений для производных токов всех элементов схемы, подключенных к шинам рабочего питания.
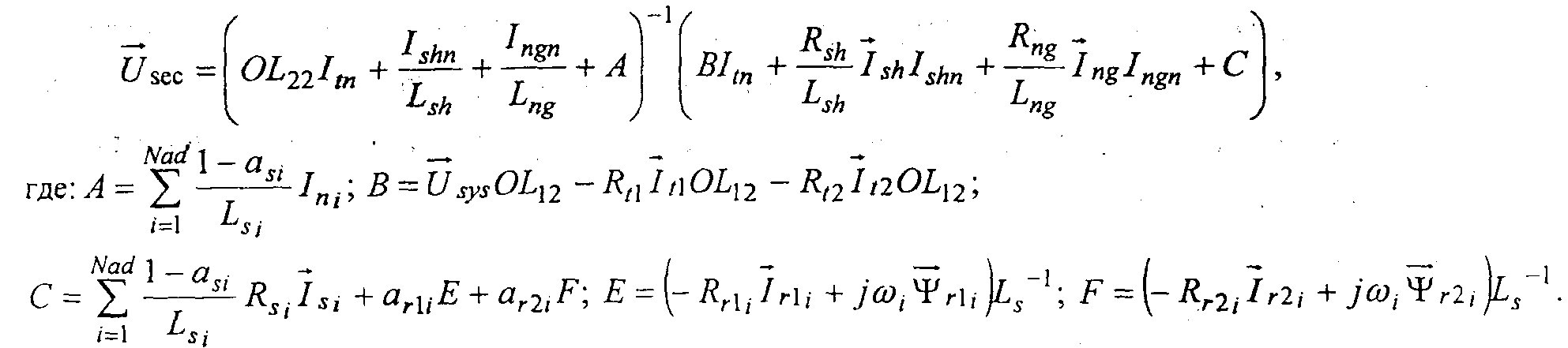
Один из путей моделирования тока подпитки места к.з. и характера протекания переходного процесса заключается в численном решении приведенных выше систем дифференциальных уравнений. Этот метод обладает достаточной точностью и может, служит в качестве эталонного. Однако, его недостаток заключается в сложности подготовки исходных данных, т.к. по каждому двигателю, число которых может достигать 20 и более на одной секции, требуется большой объем сведений для синтеза параметров схемы замещения методом
минимизации. Поэтому рассмотрим возможность использования только одного эквивалентного двигателя (ЭД) с.н. подобно рекомендуемого в ГОСТ [I], параметры которого найдем на основе моделирования по приведенным выше дифференциальным уравнениям для различного состава двигателей.С указанной целью выполним моделирование тока к.з. при различной его удаленности для двух случаев:
когда к секции подключены 7 двигателей, которые учитываются по дифференциальным уравнениям и параметры которых указаны в таблице 1, и когда к секции подключен только один эквивалентный двигатель (в табл. 1 параметры всех АД указаны в о.е. при базисном номинальном, а для ЭД при базисном пусковом сопротивлениях).
Таблица 1 - Параметры АД блок 200 МВт
|
Обозначение Двигателя |
Рп, кВт |
Tj .с |
Параметры статора и цепи намагничивания, о.е. |
Параметры ротора, о.е. |
|||||
|
Rs |
Lσ s |
L μ |
Rr1, |
Lri |
Rr2 |
Lr2 |
|||
|
ПЭН |
3800 |
4,54 |
0,0052 |
0,0782 |
2,78 |
0,0072 |
0,1369 |
0,0615 |
0,0967 |
|
ЦЭН |
1700 |
2,85 |
0,0093 |
0,0524 |
2,34 |
0,0211 |
0,2149 |
0,2570 |
0,3510 |
|
д |
1500 |
10,77 |
0,0102 |
0,1164 |
1.98 |
0.0061 0,1425 |
0,0611 |
0,1070 |
|
|
MB |
800 |
8,10 |
0,0098 |
0,1196 4.69 |
0,0119 0,1330 |
0,0797 |
0,0868 |
||
|
ДВ |
630 |
52,47 |
0,0093 |
0,1110 |
3,02 |
0,0092 0,1329 |
0,1013 |
0,1620 |
|
|
кэн |
250 |
1,83 |
0,0093 |
0.1159 |
4,02 |
0,0152 0,0873 |
0,1160 |
0,0745 |
|
|
вгд |
240 |
11,75 |
0,0092 |
0,1594 |
2,87 |
0,0197 0,1305 |
0,0887 |
0,0461 |
|
|
ЭД |
8920 |
9,088 |
0,0640 |
0,6000 |
18,0 |
0,0690 0,9470 |
1,1170 |
1,8010 |
|
По существующей методике ГОСТ [1] рекомендует учитывать ток подпитки как состоящий из периодической и апериодической составляющих, затухающих соответственно с постоянными времени
Td'
= 0,07с и Ta= 0,04с. Амплитудные значения обеих составляющих (периодической и апериоди-ческой
) принимаются равными (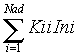 ) сумме пусковых токов двигателей, а
) сумме пусковых токов двигателей, а
огибающие амплитудных значений тока подпитки места к.з. находятся как i(t)=
В качестве примера на рис.2 приведены результаты расчеты токов к.з. по полным дифференциальным уравнениям по изложенной методике для группы из 7 двигателей (см. табл. 1) при близком к.з.
Согласно рис.2 амплитудные значения тока подпитки для соответствующих времен составляют (см. табл.2).
Таблица 2
– Амплитудные значения тока подпитки|
Амплитудные значения, о.е. |
8,444 |
6,081 |
4,592 |
3,459 |
2,575 |
1,882 |
|
Время t,с |
0,01 |
0,03 |
0,05 |
0,07 |
0,09 |
0,11 |
Огибающую амплитудных значений апериодической ( А
1), периодической переходной (a2 ) и сверхпереходной ( A3) составляющих и соответствующие постоянные времени Ta, T’ и Т" можно представить как сумму трех затухающих экспонент с различными амплитудами и постоянными времени:
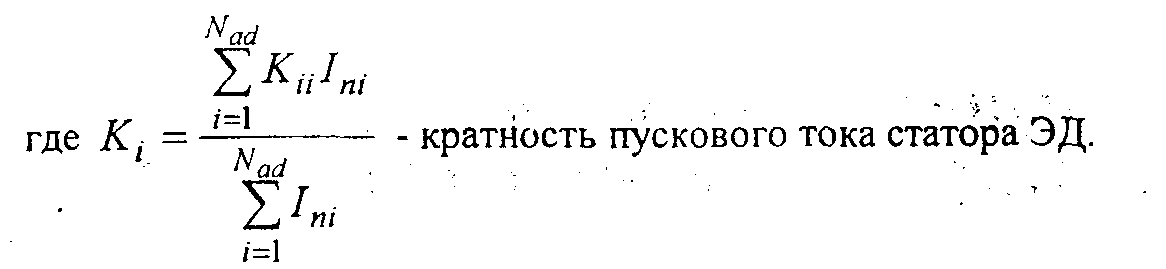
Используя данные табл.2 и уравнение (1) методом минимизации находим значения A1=1,0; .A2 =0,6;
A3=0,2; Ta
=0,06 с; T'=0,07 с и T"=0,006 с. Эти значения позволяют определить параметры эквивалентного глубокопазного двигателя используя известные [2] соотношения: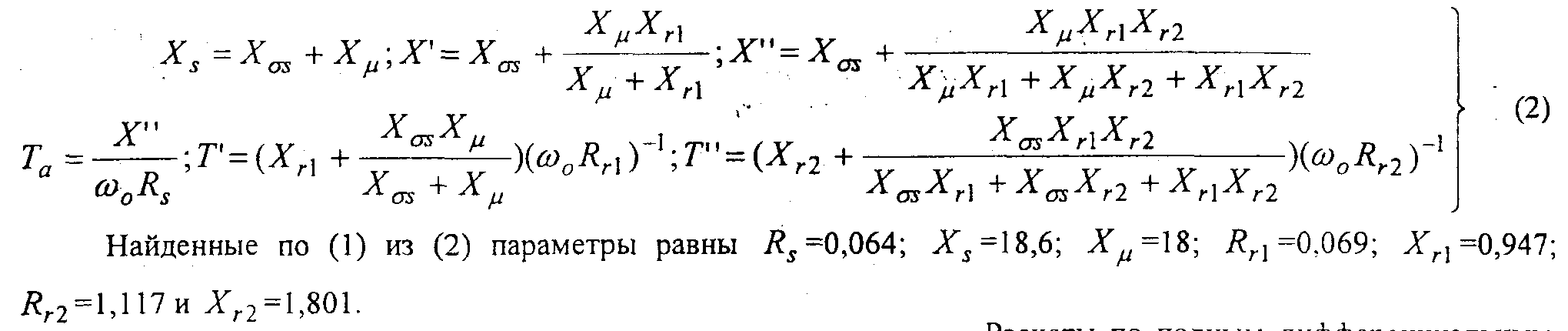
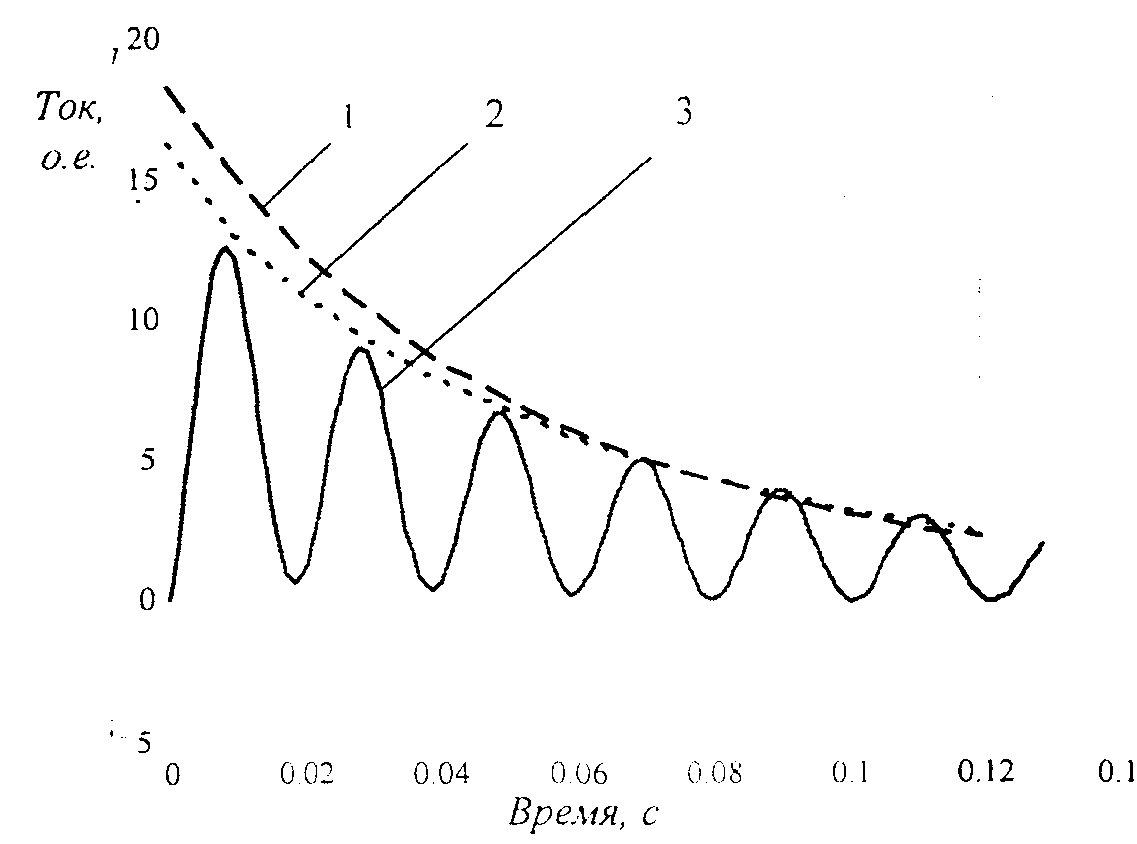
Рисунок 2
– Сравнительный анализ результатов расчета токов к.з. секции с.н.1 -расчет по методике ГОСТ [I],
2 -расчет по изложенной .методике (1);
3 -расчет по полным дифференциальным
Расчеты по полным дифференциальным уравнениям для различного состава двигателей и для блочных агрегатов мощностью 200, 300 и 800 МВт показали, что огибающая амплитудных значений по (1) может быть принята для всех случаев состава двигателей при условии использования конкретного значения суммы пусковых токов двигателей.
На рис.2 приведена для сопоставления с точным решением (кривая 3) огибающая амплитудных токов подпитки, рассчитанная по ГОСТ (кривая 1) и предложенной по (1) эквивалентной характеристике (кривая 2).
Как видно из приведенных данных погрешность в оценке тока подпитки по кривой ГОСТ достигает 25%, а по предложенной методике не превышает 7%. Более высокая точность по (1) достигнута за счет того, что группа глубокопазных двигателей заменена эквивалентным глубокопазным двигателем,
у которого кроме переходной составляющей тока учитывается и сверхпереходная. Уравнение (1) может быть рекомендовано для широкого применения как уточняющее методику ГОСТ.ВЫВОДЫ
1. Изложена методика моделирования на ПЭВМ токов к.з. в системе с.н. электростанции по полным дифференциальным уравнением всех ее элементов.
2. Для расчета тока подпитки места к.з. от группы АД по эквивалентным обобщенным характеристикам предложено выражение (1), отличающееся от имеющегося в ГОСТ наличием сверхпереходной составляющей тока, что позволяет повысить точность определения тока в системе с.н. электростанции, где используются, как правило, глубокопазные АД.
ЛИТЕРАТУРА
1. ГОСТ-27514-67. Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением свыше 1 кВ. -40 с.
2. Сивокобыленко В. Ф., Павлюков В.А. Метод эквивалентирования и расчет короткого замыкания в системе асинхронных машин. Электричество, №1, 1979. с.45-50.
3. Жуков В. В. Короткие замыкания в узлах комплексной нагрузки электрических систем. / Под ред. А.Ф. Дьякова. - М.: Издательство МЭИ, 1994. - 224 с.
4. Сивокобыленко В. Ф., Костенко В. И. Математическое моделирование электродвигателей собственных нужд электрических станций. Донецк, ДПИ, 1979, 110с.
5. Сивокобыленко В. Ф., Совпель В.Б, Павлюков В.А. Метод определения эквивалентных параметров машин переменного тока. Известия АН СССР. Сер. Энергетика и транспорт, №2, 1975. с.93-97.