РАСЧЕТ НА ПЭВМ ТОКОВ КОРОТКИХ ЗАМЫКАНИЙ ДЛЯ
ВЫБОРА УСТАВОК РЕЛЕЙНОЙ ЗАЩИТЫ ЭЛЕКТРОСТАНЦИЙСивокобыленко В. Ф; Меженкова М.А.
Донецкий государственный технический университет
В настоящее время на электростанциях (ЭС) и в энергетических системах получают применение быстродействующие микропроцессорные устройства релейной защиты (РЗ), реагирующие на мгновенные значения величин. Для оценки поведения таких защит и выбора уставок их срабатывания требуются расчеты мгновенных значений токов и напряжений в электрических сетях, особенно это важно для мощных системных узлов, какими являются блочные электростанции с агрегатами единичной мощностью 200-800 МВт.
Существующие методики расчета токов коротких замыканий (КЗ) для выбора уставок РЗ, как правило основаны на использовании кривых затухания токов [I]. Приближенный учет параметров генераторов и других элементов системы, изменений их скоростей, особенностей систем возбуждения и некоторых других факторов при таком подходе не только вносит погрешности в расчеты токов КЗ, но, в ряде случаев, не позволяет оценить поведение защит (например, работу резервной максимальной токовой защиты генератора с системой самовозбуждения при близких КЗ).
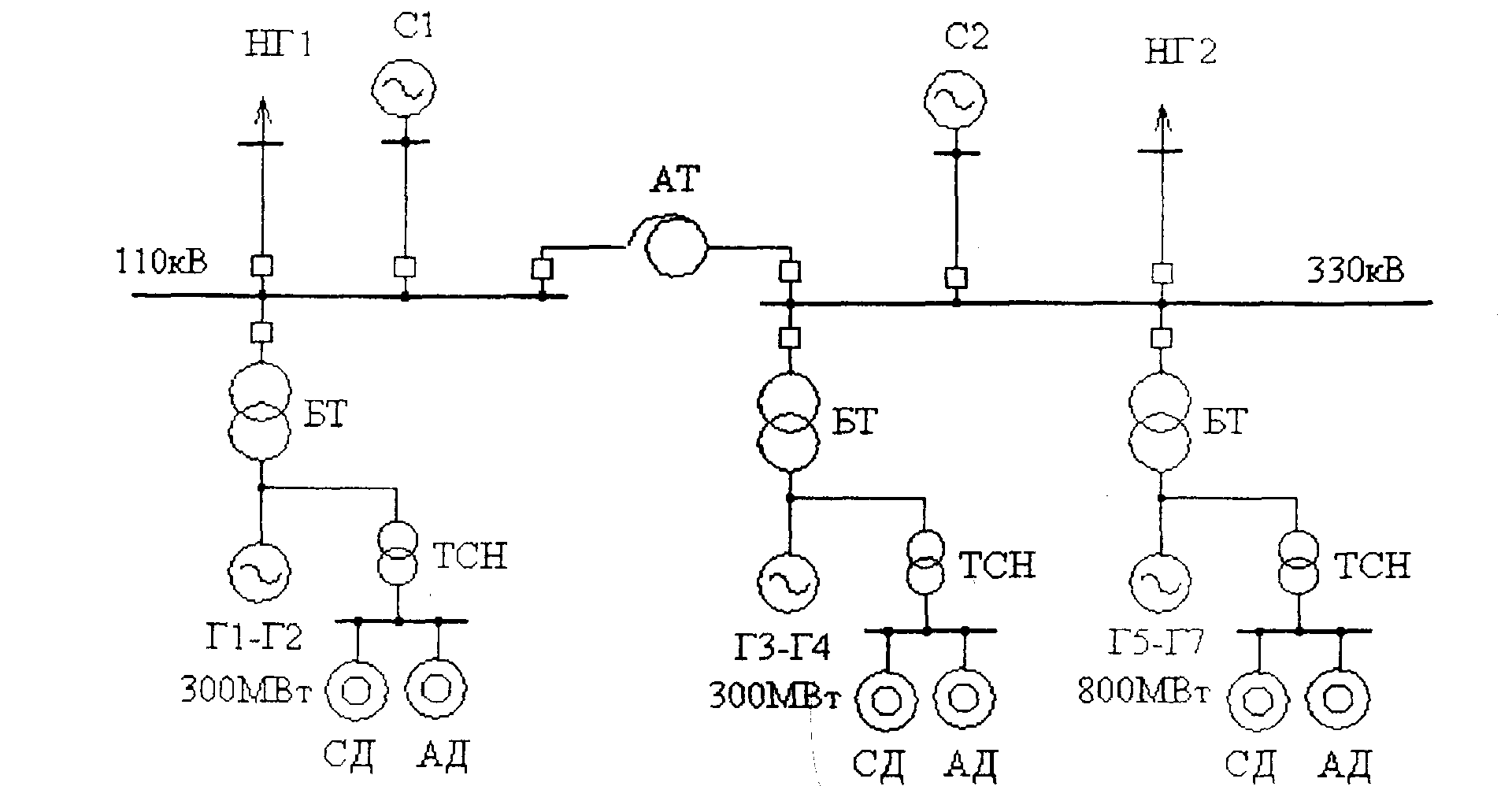
Для решения вышеуказанных проблем разработана и реализована на ПЭВМ математическая модель типовой блочной электростанции показанной на
рис 1
Рисунок 1 - Схема моделируемой электростанции
1На станции имеется два уровня напряжения 110 и 330 кВ, соединенные автотрансформаторной связью. К системе шин 110 кВ присоединены два энергоблока турбогенератор-трансформатор мощностью 300 МВт каждый. К системе шин 330 кВ подключены два энергоблока по 300 МВт и три энергоблока по 800 МВт. Нз каждом блоке учтена двигательная нагрузка собственных нужд, включающая синхронные и асинхронные двигатели. От каждой системы шин отходят линии связи с электрической системой, а также тупиковая линия с активно-индуктивной нагрузкой. Генераторы 300 МВт снабжены системами самовозбуждения, генераторы 800 МВт - системами независимого возбуждения. Имеется возможность изменять загрузку генераторов, их кратность форсировки, состав двигателей собственных нужд, мощность электрической системы.
Математические модели генераторов, трансформаторов, двигателей, линий электропередачи описаны полными дифференциальными уравнениями Парка-Горева. Уравнения асинхронных двигателей записаны в
неподвижных осях d и q. Уравнения трансформаторов и линий записаны в трехфазной системе координат а,Ь,с, учтена группа соединения блочных трансформаторов Y-Δ с заземленной нейтралью. Уравнения генераторов и синхронных двигателей записаны в собственных осях d,q, зависящих от углового положения ротора. На каждом шаге производится пересчет переменных к осям а,Ь,с. Для учета вытеснения тока массивы роторов генераторов и двигателей представлены двумя эквивалентными демпферными контурами по каждой из осей d и q, а также обмоткой возбуждения по оси d для синхронных машин. Более подробное описание математических моделей элементов приведено в [2,3].Для определения напряжений в узлах схемы используется метод Гаусса. Для определения токов в ветвях потокосцеплений вращающихся машин на каждом шаге расчета с помощью метода Рунге-Кутта система дифференциальных уравнений, записанных на основании первого закона Кирхгофа для производных токов. Режим короткого замыкания моделируется подключением шунта в месте КЗ.
Предлагаемая программа позволяет получать мгновенные значения токов, напряжений, мощностей в каждой фазе, а также обобщенные вектора этих параметров по трем фазам, углов, описывающих поведение системы; действующие значения токов и напряжений по трем фазам; токи и напряжения прямой, обратной и нулевой последовательностей.
Моделировались 1,2,3-фазные и 2-фазные на землю короткие замыкания на выводах генераторов, на системах шин 110 и 330 кВ, на секциях собственных нужд 6 кВ, на отходящих от шин линиях электропередачи.
Далее приведены некоторые осциллограммы, полученные при моделировании ЭС, аналогичной Углегорской. Полученные результаты сравнивались с имеющимися на Углегорской ТЭС расчетноэкспериментальными данными.
На рис. 2-4 показаны осциллограммы мгновенных значений токов в месте замыкания в каждой из фаз при возникновении в момент времени 0.02 с 3-фазного КЗ на шинах 110 кВ. Максимального значения 108.6 кА достигает ток в фазе С. Апериодическая составляющая в фазных токах к моменту отключения выключателей (0.2 с) еще имеет существенную величину.
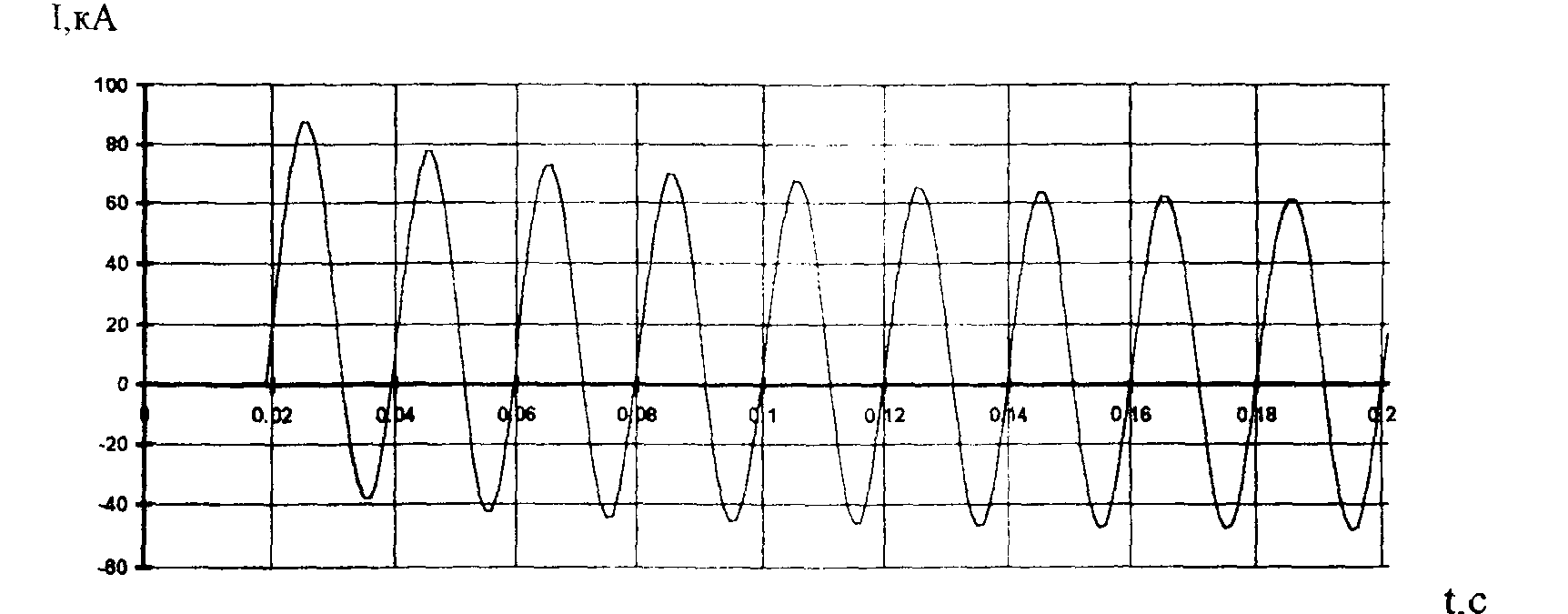
Рисунок 2 - 3-фазное КЗ на шинах 110 кВ, ток в месте КЗ,
фаза А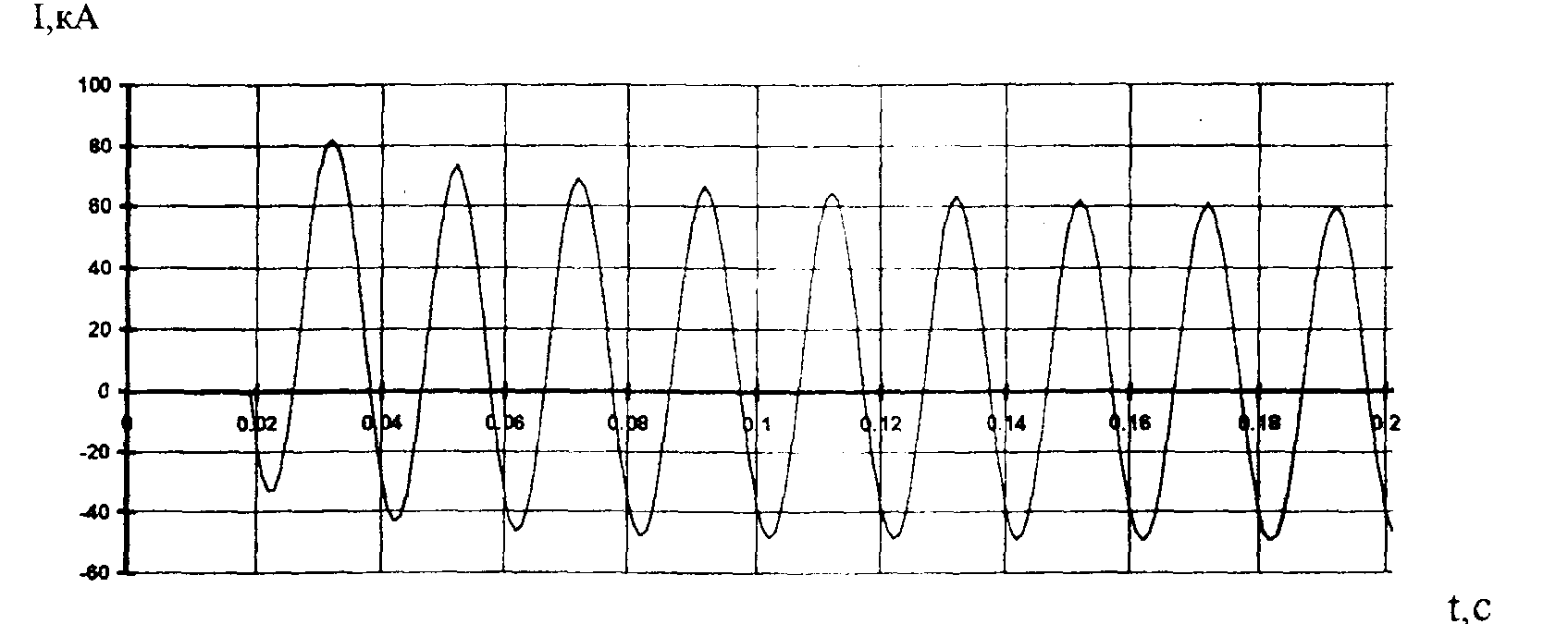
Рисунок 3 - 3-фазное КЗ на шинах
110 кВ. ток в месте КЗ. фаза В
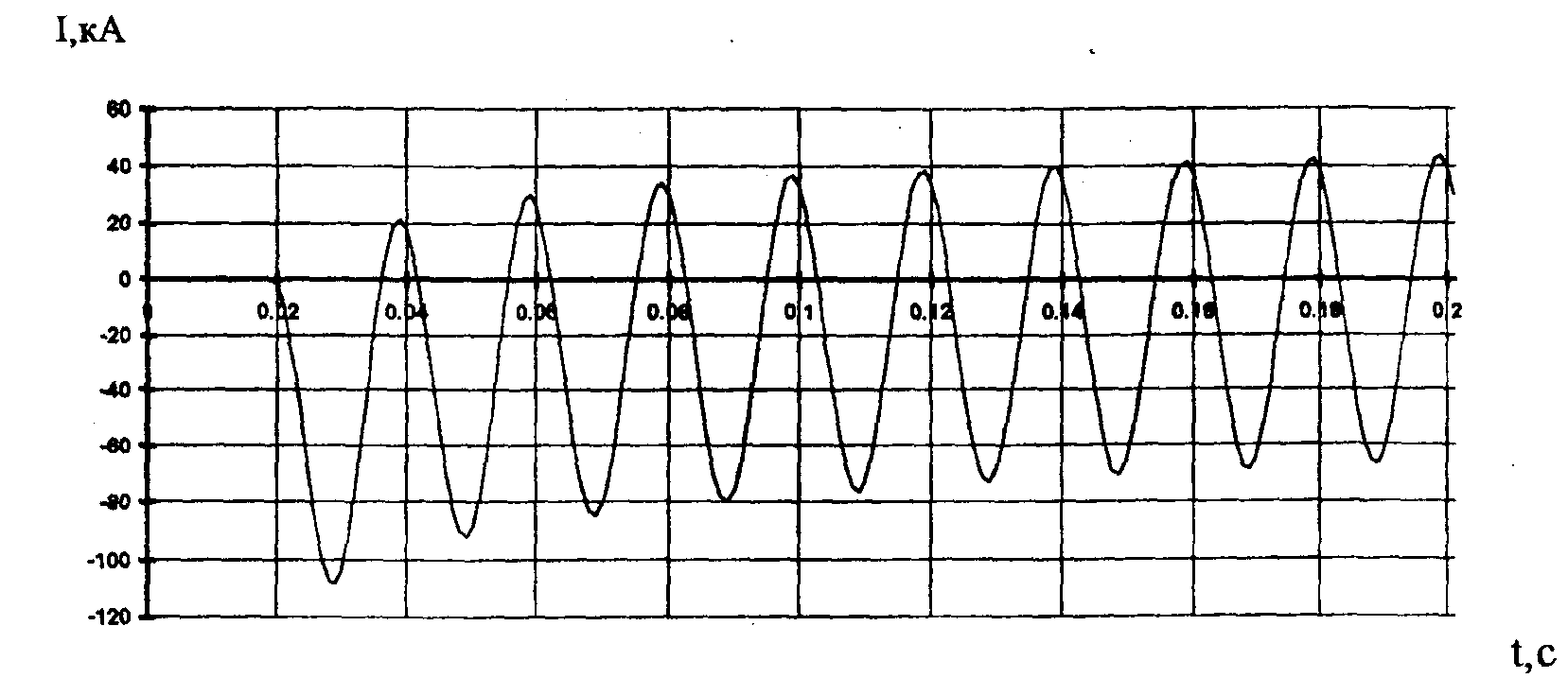
Рисунок 4 - 3-фазное КЗ на шинах 110 кВ, ток в месте КЗ, фаза С
Ток можно представить в виде вектора, вращающегося с синхронной скоростью в координатах
a,b,c, проекции которого на оси в каждый момент времени являются мгновенными значениями тока в фазах a,b,c. Такой вектор называется обобщенным или результирующим. На рис. 5 показано, как изменяется его модуль при рассматриваемом КЗ. Амплитудное значение равно 108.6 кА. Начальное значение периодически составляющей 66.5 кА, а по расчетам, предоставленным Углегорской ТЭС, эта величина равна 67.83 kA. Соответствующие действующие значения токов при 3-фазном КЗ на шинах 330 кВ составляют 50.5 и 51.54 кА.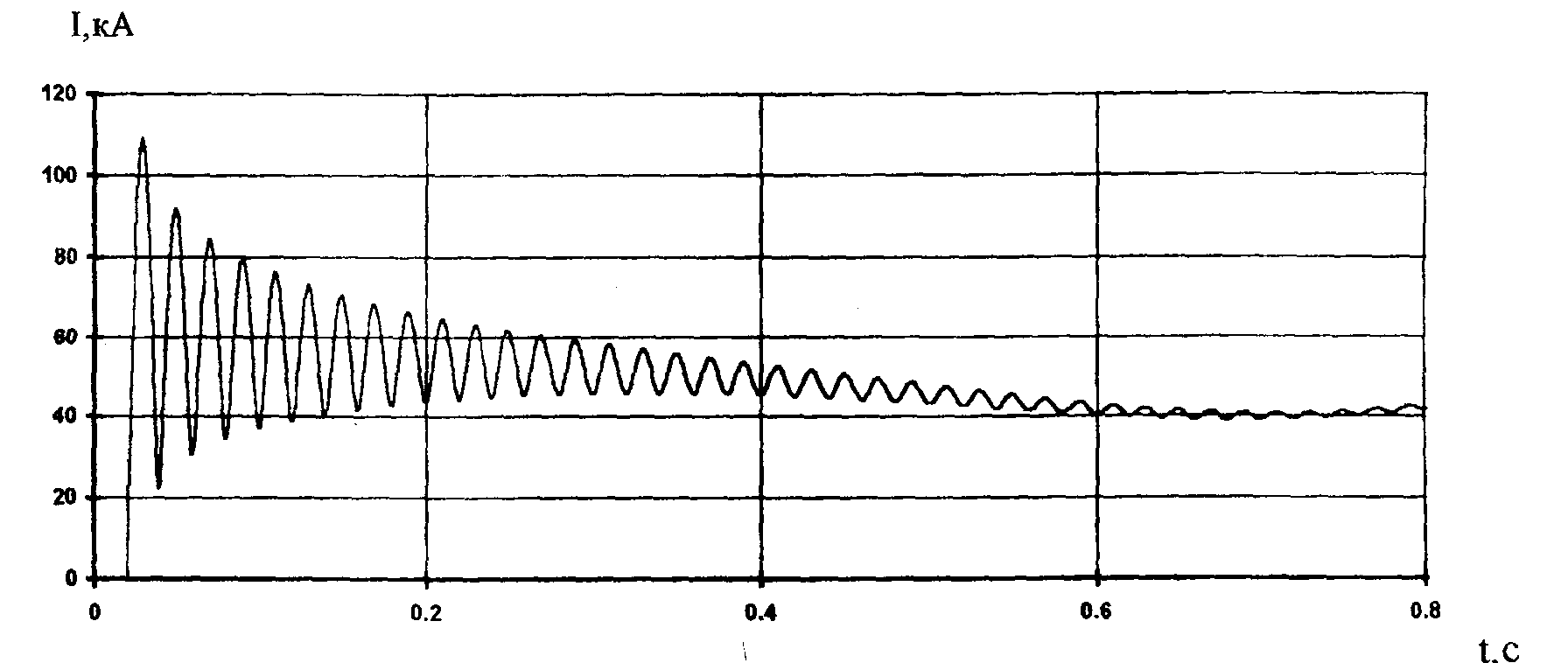
Рисунок 5 - 3-фазное КЗ на шинах 110 кВ, ток в месте КЗ. обобщенный вектор
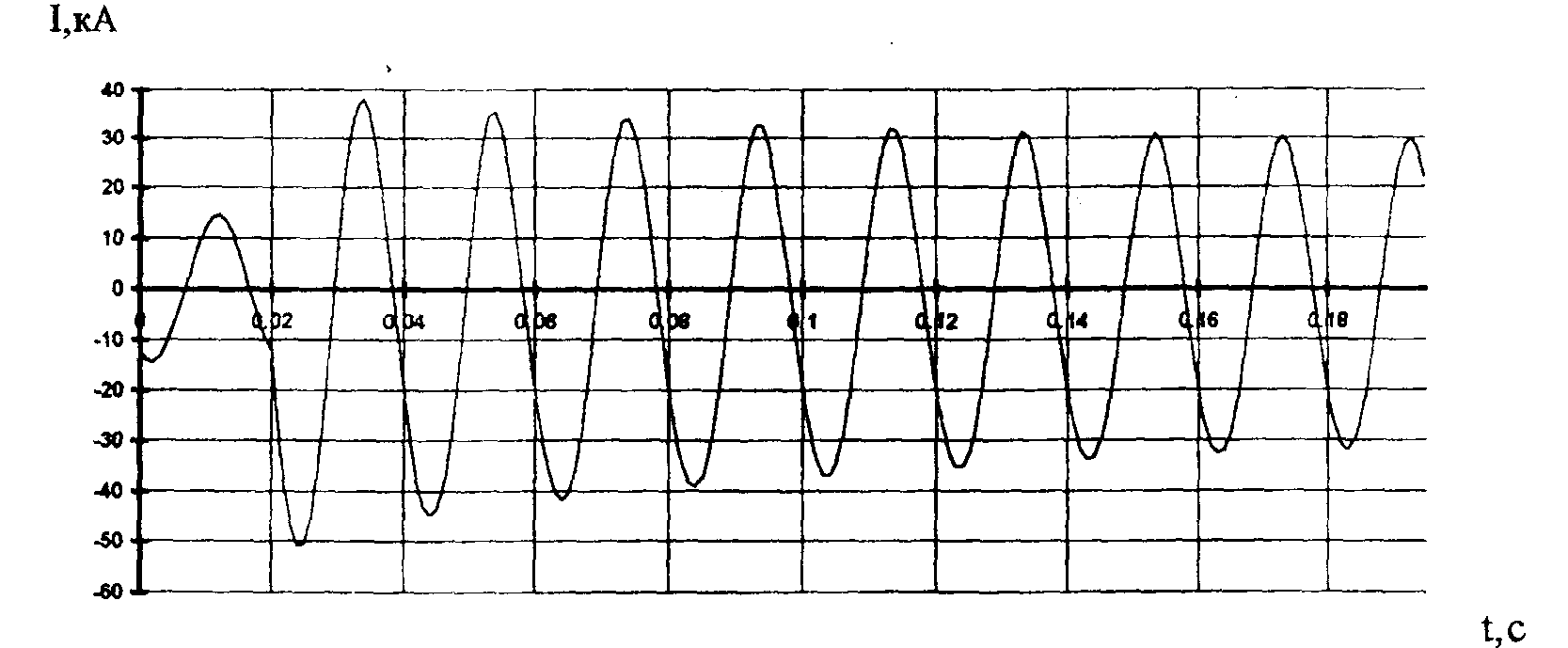
Рисунок 6 - 3-фазное КЗ на шинах 110 кВ, ток фазы А генератора
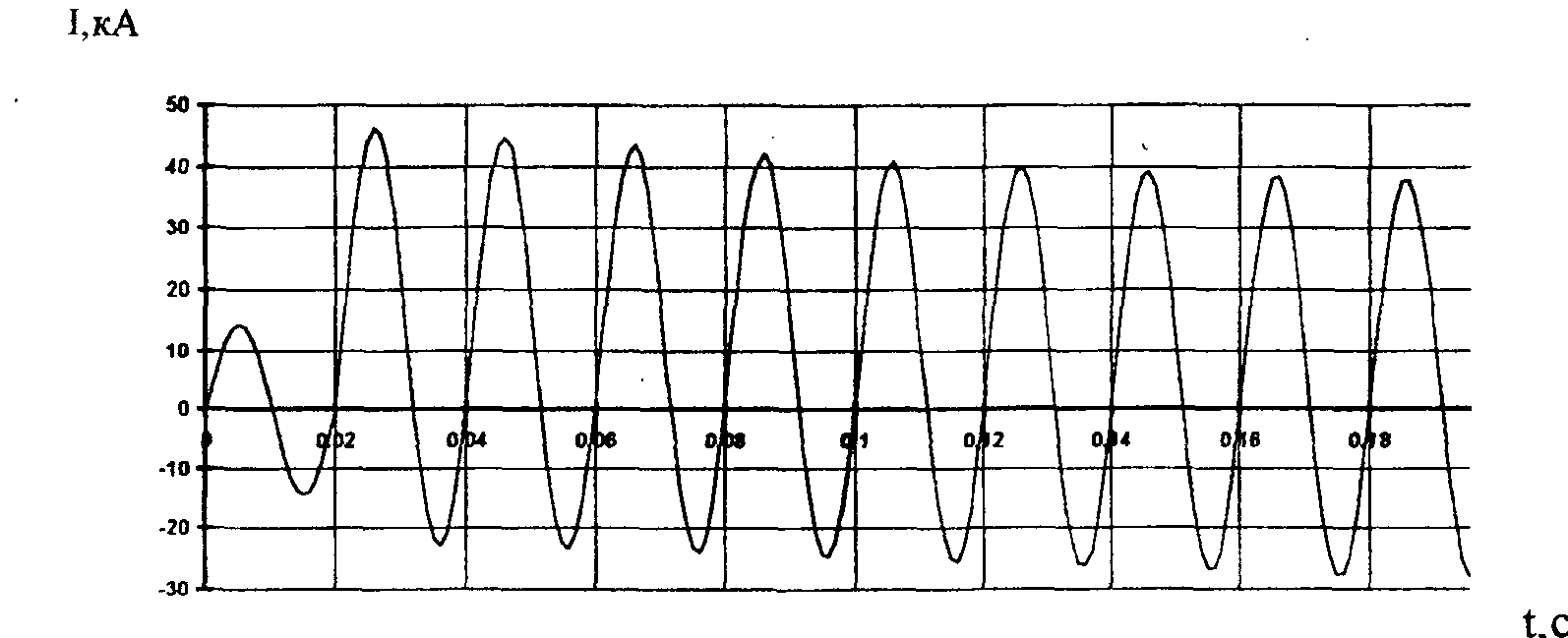
Рисунок 7 - 1-фазное КЗ на
шинах 110 кВ, ток фазы С генератора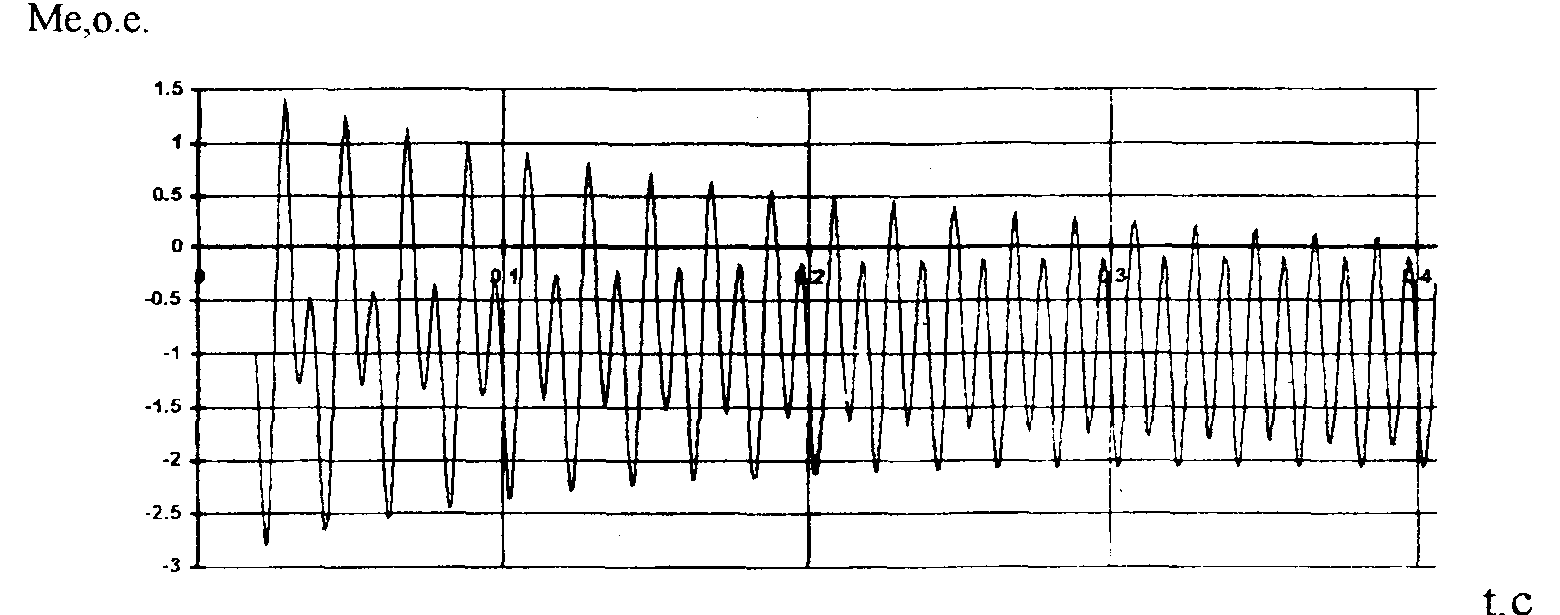
Рисунок 8- 1-фазное КЗ
на шинах ПО кВ, момент на валу генератора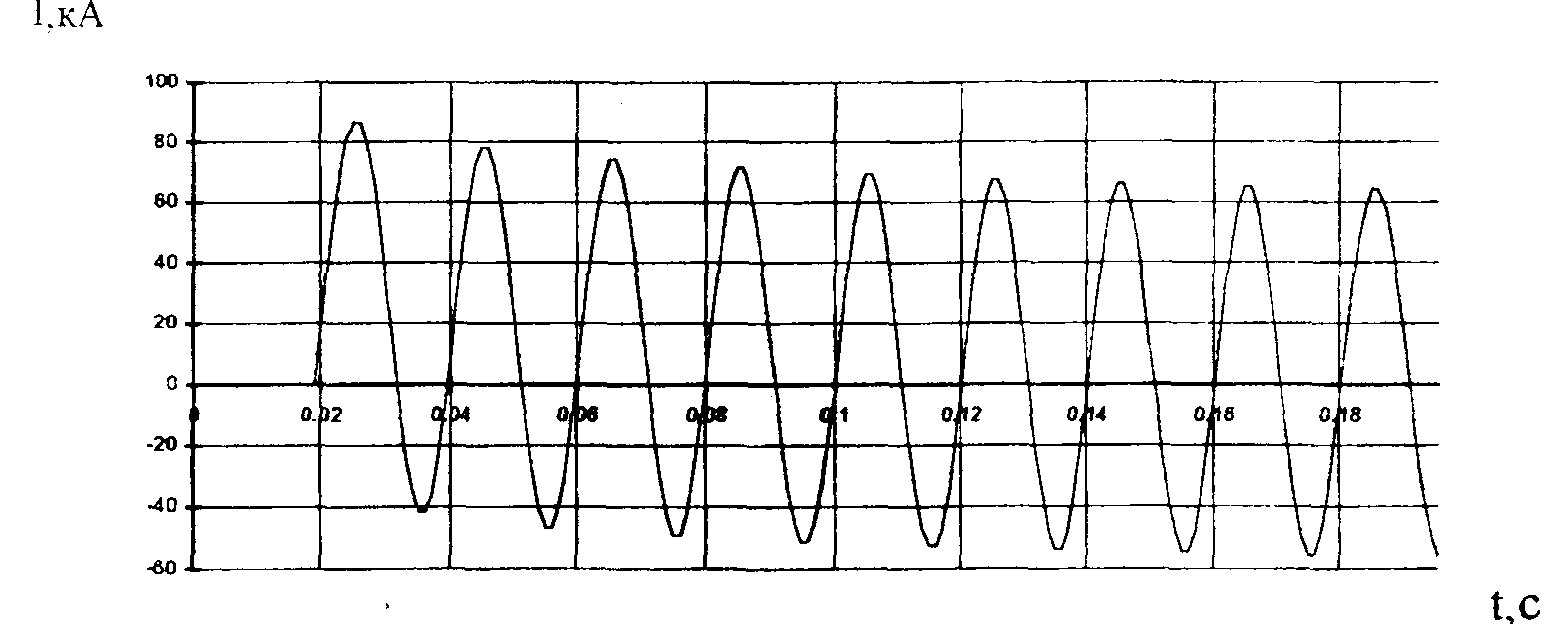
Рисунок 9 - 1 -фазное КЗ на шинах 110кВ, ток в месте КЗ в поврежденной фазе
Разработанная модель позволяет рассмотреть поведение всех элементов электростанции при различий коротких замыканиях, получить токи и напряжения во всех ветвях схемы, определить мощности. Имея характер переходного процесса, можно рассчитать уставки релейной защиты, проанализировать работу установленных защит. Результаты, полученные при моделировании, согласуются с данными Углегорской ТЭС, что подтверждает адекватность модели.
ЛИТЕРАТУРА
1.
Ульянов С.А. Электромагнитные переходные процессы в электрических системах. - М.: Энергия, 1970.-520С.2. Сивокобыленко В.Ф., Меженкова М.А. Математическая модель электрической станции для анализа поведения турбогенераторов с системами самовозбуждения при коротких замыканиях. "Техтчиа електродинам1ка" спец. Випуск за матер1алами П МЬкнародно!" науково-техтчно!' конференцп "Математичне моделювання в електротехнивд та електроенергетнщ". Кюв, 1нститут електродинам1ки НАН Украини, 1998.
3. Сивокобыленко В.Ф. Переходные процессы в многомашинных системах электроснабжения! электрических станций. - Донецк: ДПИ, 1984.- 115с.