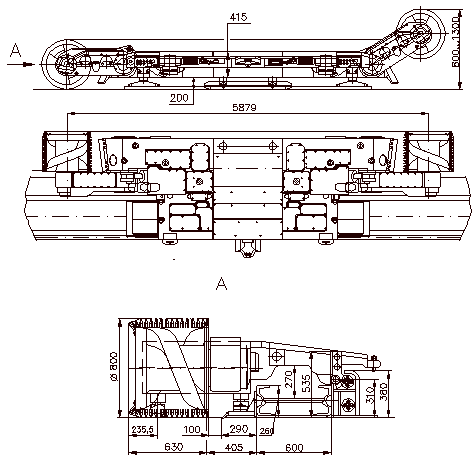
Рисунок 1.1 Общий вид комбайна УКДЗ
Научный руководитель: д. т. н., проф. Семенченко А. К.
Факультет энергомеханики и автоматизации
В современных условиях рыночной экономики перед Украиной стоит задача создания горношахтного оборудования качесивенно нового технического уровня, соответствующего мировым стандартам и способного конкурировать с крупнейшими мировыми производителями. Это подразумевает создание машин повышенной энерговооруженности и надежности, обеспечивающих высокие показатели производительности и наработки на отказ. Что может быть достигнуто повышением основных показателей качества горных машин и комплексов на всех этапах их жизненного цикла, и прежде всего на стадии проектирования, путем использования прогрессивных методов конструирования. К ним относятся современные методы обоснования рациональных структур и параметров горных машин на базе системного подхода и широкого использования систем автоматизированного проектирования (САПР), которые позволяют произвести анализ и синтез исследуемого объекта и на их основании сделать вывод о требуемой (возможной) структурной или (и) параметрической оптимизации.
Одним из основных способов повышения надежности очистных комбайнов (ОК) является снижение их динамической нагруженности и в первую очередь - электромеханической подсистемы привода исполнительных органов (ППО). Для выявления закономерностей формирования, анализа, прогноза и оптимизации динамической нагруженности силовых элементов горных машин необходимо располагать адекватными матаматическими моделями (ММ) этих динамических систем. Поэтому в данной работе производится разработка имитационной ММ для изучения динамических процессов в ППО нового ОК УКДЗ [1, 9].
Согласно [1, 2, 3] эквивалентная динамическая модель электромеханической системы привода исполнительного органа комбайна УКДЗ при использовании модели двигателя с параллельно соединенными упругим и диссипативным элементами может быть представлена в следующем виде(см. рис. 3.1.1).
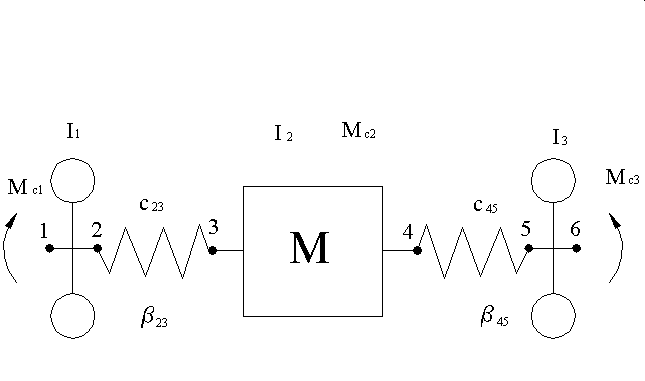
Уравнения, описывающая динамическое поведение данной системы, имеют вид:
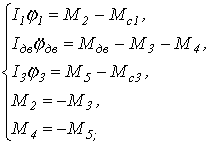(3.1)где I1 и I3 - приведеные к двигалю массовые моменты инерции 1-го и 2-го исполнительных органов, кг.м2;
Iдв - массовый момент инерции ротора двигателя с приведенными к нему моментами инерции деталей, кг.м2;
φ..1, φ..3, φ..дв - соответственно угловые ускорения указанных точек схемы и ротора двигателя, рад/с2;
Мдв - момент, развиваемый двигателем, Нм;
Мс1, Мс3 - моменты сопротивления на исполнительных органах,Н.м.
Данная динамическая модель привода включает в себя такие функционально-законченные элементы (ФЗЭ) как: "электродвигатель", "маховик" и "упругий вал". Рассмотрим математические модели каждого элемента.
Динамические процессы в двигателях, в том числе на нелинейной части характеристики, с учетом общеизвестных допущений наиболее полно описывают ММ , разработанная на основе фундаментальных исследований Парка - Горева [7, 8, 9]. Особенностью комбайновых двигателей с глубокопазными роторами является необходимость учета изменения параметров схемы замещения двигателя в зависимости от скольжения S, что связано с явлением вытеснения токов в поверхности стержней, для учета чего произведена замена контура ро-тора с параметрами Xr и Rr(S) эквивалентным двойным контуром с параметрами Xrb, Xrн и Rrb, Rrн не зависящими от S. Тогда ММ электродвигателя может быть записана.
Расчетные параметры:
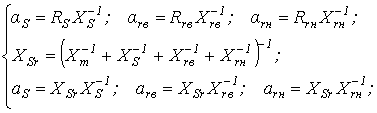(3.2)
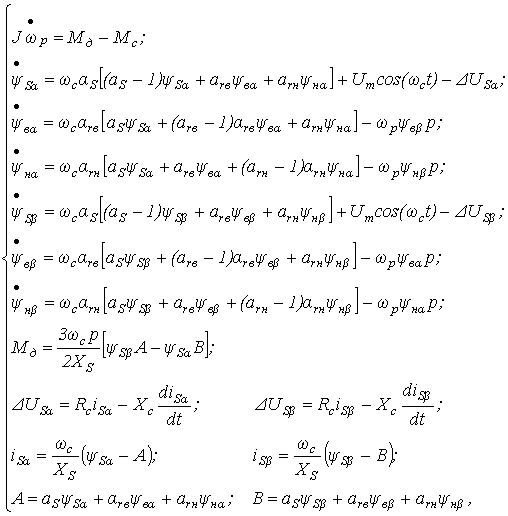(3.3)где ΔUSβ, ΔUSα - падения напряжений;
Rc, Xc - соответственно активное и индуктивное сопротивление питающей сети;
iSα, iSβ - токи статора в проекции на оси α и β;
ωс - угловая скорость магнитного поля;
Um - амплитуда напряжения в фазе;
Мд, Мс - соответственно моменты двигателя и сопротивления;
р - число пар полюсов;
ωр - угловая скорость ротора электродвигателя;
Rs, Xs, Rrb, Xrb, Rrh, Xrh, Xm - параметры схемы замещения.
ММ асинхронного электродвигателя может быть записана в виде неявной вектор-функции:
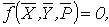
где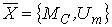
- входной вектор;
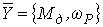- выходной вектор;
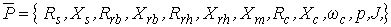- вектор параметров.
Математическая модель маховика отражает инерционные свойства исполнительного органа либо любой другой вращающейся массивной части трансмиссии и может быть записана:
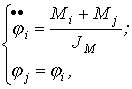(3.4)где Mi,Mj - вращающие моменты в точках соединения маховика с элементами трансмиссии, Нм;
φi, φj - углы поворота точек соединения маховика с элементами трансмиссии, рад;
JM- момент инерции вращающейся массы, кгм2.
ММ ФЗЭ "маховик" в интегрированной форме может быть представлена в виде явной вектор-функции:
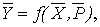,где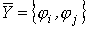 
- выходной вектор ФЗЭ;
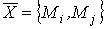- входной вектор ФЗЭ;
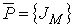- вектор параметров ФЗЭ.
Математическая модель упругого вала отражает жесткостные свойства элементов трансмиссии и может быть представлена в виде:
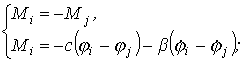(3.5)где Mi,Mj - упругие моменты, прикладываемые к концам вала, Нм;
φi, φj, φ.i, φ.j- углы поворота и их производные (скорости) сечений вала в точках i и j, рад, рад/с;
c - жесткость упругого вала, Нм/рад;
β - коэффициент рассеивания энергии упругим валом (коэффициент диссипативных потерь), Нмс.
ММ ФЗЭ "упругий вал" в интегрированной форме может быть представлена в виде явной вектор-функции:
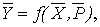,где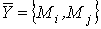 
- выходной вектор ФЗЭ;
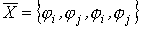- входной вектор ФЗЭ;
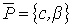- вектор параметров ФЗЭ.
Тогда, согласно (3.2) - (3.5), уравнения (3.1) могут быть представлены в удобном для реализации в пакете MathLAB 5.3, среде Simulinc 3.0:
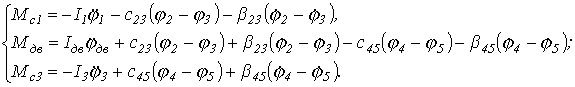
При расчете инерционных характеристик рассматриваемые детали и сборочные единицы простой конфигурации аппроксимировались совокупностью цилиндрических и конических участков. При этом моменты инерции I, кг.м2 цилиндров и конусов определялись согласно [2, 3, 4, 5] по выражениям:
для полого цилиндра
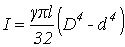, где γ=7,8 .103 кг/м3- плотность стали;
l, D, d- соответственно длина, наружный и внутренний диаметры цилиндра, м;
для усеченного конуса
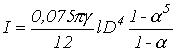, где
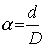. Детали сложной конфигурации- лопасти шнека - и сосредоточенные массы- кулакии и резцы - аппроксимировались в виде цилиндрических дисков из условия равенства занимаемого объема.
3.2.2 Определение жесткостных характеристик элементов привода
Жесткость элементов определяется как величина, обратная податливости. Согласно экспериментальным исследованиям, выполненным рядом авторов[1, 3, 4], зубчатые редукторы выемочных комбайнов обладают значительной результирующей податливостью. Эта податливость определяется не только крутильными деформациями валов, но в ряде случаев оказывается существенно зависящей от деформации опор валов, корпусов и зубьев колес. Поэтому полная податливость определяется суммой эквивалентной приведенной к крутильной и крутильной податлиостей.
Крутильная податливость типичных элементов, испозуемых в комбайновом приводе орпеделяется по следующим зависимостям.[2, 3]
Податливость вала на кручение
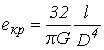, где D - диаметр вала, м;
G - модуль сдвига, для стали G = 8.1010 Н/м2;
l - длина вала, равная расстоянию между точками приложения крутящих моментов, м.
Крутильная податливость шлицевых соединений
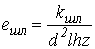, где d = dср - средний диаметр соединения, м;
l - рабочая длина соединения, м;
h - активная высота шлица, м;
z - число шлицев;
kшл = 4.10-12, м3/Н - для шлицевого соединения.
Приведенная к одному из валов крутильная податливость зубчатой передачи определяется изгибными и контактными деформациями зубьев
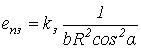. гдеkз - упругая деформация пары зубьев при действии единичного нормального давления, приложенного на единицу ширины зуба. Для стальных прямозубых колес kз = 6.10-12 м/Н;
R - радиус начальной окружности зубчатого колеса, расположенного на валу, к которому приводится податливость передачи (для конических колес R - среднее значение радиуса начальной окружности, м;
b - рабочая ширина колеса, м;
α - угол зацепления.
Податливость опор с подшипниками качения определяется в основном упругим сближением тел качения δ',м и контактными деформациями в местах посадки колец на вал или в корпус δ", м [2, 3, 4, 5, 6, 11]. При этом суммарная деформация δ, м
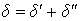, где
для роликового радиального двухрядного сферического
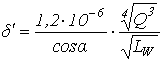, радиально-упорного конического
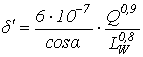, где
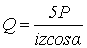; для шарикового упорного одинарного
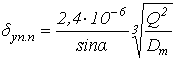, где
; 
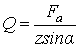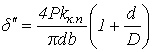. Здесь Q - величина радиальной нагрузки, воспринимаемая наиболее нагруженным телом качения, даН;
P - радиальная нагрузка на подшипник, даН, Н;
i - число рядов тел качения;
z - число тел качения в ряду;
α - угол контакта, град;
LW - рабочая длина ролика, мм;
Dт - диаметр тела качения,мм;
Fa - осевая нагрузка на подшипник, даН, Н;
D, d, b - соответственно наружный и внутренний диаметры подшипника, ширина подшипника, м;
kк. п = 1.10-12 м3/Н - коэффициент контактной податливости.
Тогда податливость подшипниковой опоры eп, м/Н
для радиальных и радиально-упорных подшипников
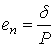, для упорных
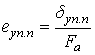. Изгибная податливость валов определяется с помощью так называемых коэффициентов влияния α и γ (коэффициентов перемещений), рассматриваемых в сопротивлении материалов и в строительной механике. Общие выражения для расчета этих коэффициентов даны в работах [4, 5].
Схема расчета эквивалентной крутильной податливости следующая [2, 4].
1. Определяют силы, действующие на зубчатые колеса.
2. Определяют суммарный прогиб вала y-i под зубчатым колесом от всех сил P-i , действующих на вал, а также перемещение колеса δ-i , вызванное податливостью подшипниковых опор.
3. Вычисляют полное линейное перемещение зубчатого колеса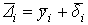 
, относительное смещение находящихся в зацеплении колес i и i+1 
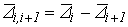и взаимный угол поворота зубчатых колес (цилиндрических), приведенный к i-му колесу:
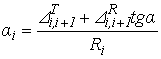, где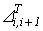 
, 
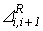- соответственно тангенциальная и радиальная проекции вектора 
.
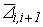4. Вычисляют эквивалентную крутильную податливость:
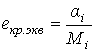. 5. Найденное значение податливости суммируют с крутильной податлиаостью шлицевых соединений, валов и зубчатых колес рассматриваемого участка схемы.
В магистерской работе определение эквивалентной податливости каждого элемента схемы производилось по методике, изложенной в [2, 3, 4, 5, 6, 11]
Приведение моментов инерции и податливостей элементов схемы ко входному валу редуктора осуществляется по зависимостям [2, 3, 4]:
; 
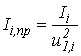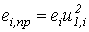. | № узла (вала) на кинематической схеме | U1,i | Ii, кг.м2 | Iiпр, кг.м2 | ei, рад/Н.м | eiпр, рад/Н.м |
|---|---|---|---|---|---|
| I II III IV V VI VII VIII IX ИО ЭД |
1,0 2,5 4,615 8,902 15,045 15,045 23,139 23,139 18,51 1 |
0,0533 0,8579 0,822 1,2807 0,938 1,4819 1,2686 1,2686 1,1954 43,8911 0,56 |
0,0533 0,1373 0,0386 0,0162 0,0041 0,0065 0,0024 0,0024 0,0035 0,1281 0,56 |
0,0000015200 0,0000022809 0,0000015425 0,0000001337 0,0000001999 0,0000004778 0,0000000119 0,0000000494 0,0000001556 |
0,00000152 0,00001426 0,00003285 0,00010592 0,00004524 0,00010815 0,00000635 0,00002645 0,00005331 |
| eсум = 0,00034055 рад/Нм; cсум = 2537,778 Нм/рад | |||||
В дальнейшем планируется реализация созданной модели в пакете MathLAB 5.3, среде Simulinc 3.0 с различными параметрами нагрузки. Также будет представлена ММ ОК как пространственной многомассовой динамической системы с математическим описанием входящих элементов: пространственно-перемещающейся массы, узлов взаимодействия масс (цилиндрический шарнир, упор, гидравлический упор, гидроцилиндр, исполнительный орган).