
Мерков А.М., Поляков Л.Е. Санитарная статистика (пособие для врачей).М.: Медицина.-1974.-384С.
Глава V.
ВАРИАЦИОННЫЙ РЯД И СРЕДНИЕ ВЕЛИИЧИНЫ.
Вариационный ряд. Кроме относительных величин (коэффициентов), характеризующих частоту (интенсивность), либо состав изучаемого явления, статистические сов окупности с их количественной стороны могут быть охарактеризованы при помощи средних величин. При изучении физического развития населения , закономерностей течения различных процессов в здоровом и больном организме, для оценки эффективности лекарс твенных препаратов и решения целого ряда других задач используются средние величины.
Средние величины получаются из рядов распределения (вариационных рядов). В таком ряду количественно изменяющийся признак носит название варьирующего, а отдельные его количественные выражения называются вариантами. Числа, показывающие, как часто встречается та или иная варианта в составе данного ряда, носят название частот. Ряд, в котором сопоставлены варианты и соответствующие этим ва риантам частоты и который, следовательно, показывает распределение изучаемой совокупности по величине какого-либо варьирующего признака, носит название вариационного ряда (распределение призывников по росту, новорожденных по весу и т.п.).
Медиана и мода. Вариационный ряд, кроме средней арифметической, может быть охарактеризован еще двумя величинами – медианой и модой.
Модой (обозначается Мо) называется та варианта, которой соответствует наибольшее количество частот вариационного ряда. По данным табл.20, мода нахо дится в интервале роста 149,0 – 152,9, так как именно этот рост имеет наиболее многочисленная группа школьников. С некоторым приближением можно принять моду равной середине этого интервала, т.е. Мо = 151,0 см.
В санитарной статистике применение моды довольно ограничено. Модой можно пользоваться для оценки средней длительности заболеваний, особенно при малом количестве больных данной болезнью. В
Том случае несколько больных с особо длинными или очень короткими сроками лечения окажут значительное влияние на величину средней арифметической величины, если воспользоваться ею для определения средней длительности заболевания. Здесь мода, т.е. обычная длительность заболевания, окажется более полезной для практического использования.
Медианой (обозначается Ме) называется варианта, делящая вариационный ряд на две равные половины, т.е. та варианта, меньше которой имеют размеры по ловины частот.
В примере из табл.21 медианой должен быть рост такой рост, меньше которого рост ![]() девочек и больше которого рост 99 девочек.
девочек и больше которого рост 99 девочек.
Медиана вычисляется при помощи так называемого начетного ряда, показанного в графе 6 табл.21.
Начетный ряд получают путем последовательного суммирования частот, расположенных в графе 2 той же табл.
Медиана применяется в санитарной статистике относительно редко. С помощью медианы определяется, например, так называемая вероятная продолжительность предстоящей жизни в таблицах смертности.
Основным отличием медианы и моды от средней арифметической является то, что на их размеры не оказывают влияния величина крайних значений вариант, имеющихся в вариационном ряду, тогда как при определении средней арифметической прини маются вовнимание значения всех вариант.
Среднее квадратическое отклонение. Вторым параметром вариационного ряда (величиной, характеризующей вариационный ряд) является среднее квадратическое отклонение, обозначаемое σ (малая греческая сигма).
Среднее квадратическое отклонение равняется квадратному корню из суммы произведений частот вариационного ряда на квадраты отклонений вариант от средней арифметической, деленной на ч исло частот:
![]() .
.
Более правильно в знаменателе подкоренного выражения ставить не n, a n-1. При достаточно большом количестве наблюдений уменьшение знаменателя на 1 не сказывается сколько-нибудь существ
енно на результате, так как после всех вычислений изменяется только величина второго или даже третьего десятичного знака. Однако при малом количестве наблюдения (примерно 30 и менее), что почти всегда имеет место при статистической обработке клинических
и лабораторно-экспериментальных материалов, это уточнение имеет значение. В этих случаях ![]()
Описанный непосредственный способ вычислений требует большой вычислительной работы. Более простой способ вычисления
σ сходен с упрощенным методом вычисления средней арифметической.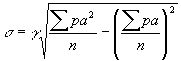 .
.
Вычисление среднего квадратического отклонения по амплитуде.
Если отсутствуют необходимые исходные данные для вычисления среднего квадратического отклонения обычным путем, может быть использован приближенный способ вычисления σ
Среднее квадратическое отклонение, исчисляемое по амплитуде, несколько отличается по величине от
σ, вычисленной обычными способами. Различие это тем больше, чем больше число наблюдений, использованных для составления вариационного ряда. Поэтому определение среднего квадратического отклонения по амплитуде более целесообразно производить преиму щественно при ориентировочных расчетах. Вычисление производится по формуле:![]()
где
ampl -амплитуда , k-коэффициент, соответствующий числу наблюдений. Определяется k по специальной вспомогательной таблице, исчисленной С.И.Ермолаевым (табл. 26). Приводим эту таблицу, заимствованную у Н.А.ТолоконцеваВ этой таблице числа
n в первом вертикальном столбце означают десятки, а в первой горизонтальной строке – единицы набюдений, например, для числа наблюдени й 87 (n=87) k =4,91, а для n = 18 k = 3,64.
Значения
k для вычисления среднего квадратического отклонения (` 3;) по амплитуде.|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 10 20 30 40 50 60 70 80 90 |
- 3,08 3,73 4,09 4,32 4,50 4,64 4,75 4,85 4,94 |
3,17 3,78 4,11 4,34 4,51 4,65 4,77 4,86 4,95 |
1,13 3,26 3,82 4,14 4,36 4,53 4,66 4,78 4,87 4,96 |
1,69 3,34 3,86 4,16 4,38 4,54 4,68 4,79 4,88 4,96 |
2,06 3,41 3,90 4,19 4,40 4,56 4,69 4,80 4,89 4,97 |
2,33 3,47 3,93 4,21 4,42 4,57 4,70 4,81 4,90 4,98 |
2,53 3,53 3,96 4,24 4,43 4,59 4,71 4,82 4,91 4,99 |
2,70 3,59 4,00 4,26 4,45 4,60 4,72 4,83 4,91 4,99 |
2,85 3,64 4,03 4,28 4,47 4,61 4,73 4,83 4,92 5,00 |
2,97 3,69 4,06 4,30 4,48 4,63 4,74 4,84 4,93 5,01 |
|
N |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
K |
5,02 |
5,49 |
5,76 |
5,94 |
6,07 |
6,18 |
6,28 |
6,35 |
6,42 |
6,48 |
Для примера, использованного в табл.20, в котором центральная наибольшая варианта равна 167 см, наименьшая – 135 см. а
n = 19 7, т.е. приближенно 200, среднее квадратичесое отклонение, исчисленное по амплитуде, равноЗначение среднего квадратического отклонения. Средняя арифметическая характеризует одной величиной весь вариационный ряд. Олнако чем больше варьирует индивидуал ьные значения вариант, тем. Очевидно, менее точно характеризуется вариационный ряд средней арифметической.
Ряд с большей амплитудой имеет большее среднее квадратическое отклонение (амплитуда приближенно равна 6 σ).
Следовательно, две олдинаковые средние , полученные из вариационных рядов с различной амплитудой, не в одинаковой степени характеризуют свои ряды. Та из них, которая имеет меньшее среднее квадратическое отклонение и, следовательно, получена из вариационного ряда с меньшей вариабельностью, своим размером будет больше приближаться к действительной величине значительного большинства единиц ряда.
Отклонение размера роста даного лица от средней величины роста всего коллектива, однородного в отношении пола, возраста, этнической и социальной принадлежности и пр., не превышающее среднего квадратического отклонения, считается на ходящимся в пределах нормы. Отклоненеие (в любую сторону) больше чем на 1σ, но меньше чем на 2σ считается субнормальным, а отклонение больлше, чем на 2σ – значительно выше или ниже среднего.
Глава V1
ВЫБОРОЧНЫЙ МЕТОД В САНИТАРНО-СТАТИЧСТИЧЕСКИХ ИССЛЕДОВАНИЯХ
Теоретические основы выборочного метода. Вся совокупность единиц, представляющая изучаемое явление – объект исследования, называется генеральной совокупностью. Часть генеральной совокупности, отобранная для обследо вания и изучения, называется выборочной совокупностью. К числу важнейших количественных характеристик выборочной совокупности относятся выборочные средние
(xˉ,y&# 713;,zˉ и т.д.) и относительные величины (частостьЧтобы определить степень точности выборочного наблюдения, необходимо оценить величину ошибки, которая может случайно произойти в процессе выборки. Такие ошибки носят название случайных ошибок презентативности
(m) и является фактически разностью между относительными показателями или средними числами, полученными при выборочном статистическом наблюдении, и аналогич ными величинами, которые были бы получены при сплошном исследовании того же объекта наблюдения.Ошибки презентативности возникают потому, что при выборочном наблюдении изучается только часть генеральной совокупности, которая недостаточно точно воспроизводит, представляет генеральную совокупность. Из этого следует, что выбороч ному наблюдению присущи ошибки репрезентативности.
Ошибки реперзентативности нельзя спутывать с ошибками регистрации, которые зависят от качества провелдения статистического наблюдения.
Сущность математиечской теории выборочного метода, основанной на теории вероятностей, сводится к тому, что она позволяет определять размер ошибки реперзентативности, оценивать точность выборочного наблюдения и обосновыват ь меры, направленные на уменьшение отклонения выборочных хараткристик от соответствующих характеристик генеральной совокупности.
Теориия выборочного метода возникла как теория случайной выборки. При случайном отборе создаютсмя условия для действия закона больших чисел и становится возможным применение теории вероятностей.
Закон больших чисел устанавливает зависимость между численностью подвергаемых наблюдению массовывх явлений и полнотой проявления общей закономерности, присущей этим явлениям. При достаточно большом числе наблюдений яснее выступают те черты и свойства, которые наиболее существенны для всех единиц данного типа.
Действие закона больших чисел проявляется в тенденции выборочной средней (частости) максимально приблизиться к генеральной средней (доле
). Разность между значениями выборочной средней (частости) и генеральной средней (доли) представляет собой, как было уже сказано, ошибку выборочного наблюдения (ошибку репрезентативности), которая может быть положительной или отрицательной, и стремится к нул ю при бесконечно большом увеличении числа наблюдений выборочной совокупности.На практике для определения средней ошибки выборки в статистических исследованиях пользуются формулами:
а) для средней ошибки средней арифметической:
![]() , (для средних)
, (для средних)
где σ – среднее квадратическое отклонение;
n
– численность выборки;б) для доли:
![]() , (для относительных величин)
, (для относительных величин)
где p - соответствующая доля (в %);
q
= 100 – p.Эти формулы, прежде всего
, справедливы для повторной выборки (с возвратом), поскольку вероятность попасть в выборку для каждо й единицы наблюдения не меняется на протяжении всего отбора.Результаты бесповторного отбора точнее, чем при повторной выборке. Ошибка репрезентативности при бесповторном отборе вычисляется по формуле:
![]() ,
,
где N – объем генеральной совокупности. Множитель ![]() всегда меньше единицы, следовательно, при прочих равных условиях, ошибка репрезентативности при бесп
овторной выборке меньше, чем при повторной. Если объем генеральной совокупности N значительно больше объема выборочной совокупности
всегда меньше единицы, следовательно, при прочих равных условиях, ошибка репрезентативности при бесп
овторной выборке меньше, чем при повторной. Если объем генеральной совокупности N значительно больше объема выборочной совокупности
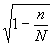 в медико-статистических работах близка к единице и ею при расчетах можно пренебречь. В таких случаях при определении ошибки случайной бесповторной выборки можно пользоваться формулой ошибки случайной повторной выборки
в медико-статистических работах близка к единице и ею при расчетах можно пренебречь. В таких случаях при определении ошибки случайной бесповторной выборки можно пользоваться формулой ошибки случайной повторной выборки
![]() .
.
При конечных размерах генеральной совокупности, если объем выборки (
n) не менее![]() .
.
Ошибки репрезентативности в механической выборке, при условии случайного размещения единиц наблюдения с точки зрения изучаемого признака, можно определять по приведенным выше формулам ошиб ки случайной бесповторной выборки.
Ошибка типической выборки определяется также по формуле ошибки случайной бесповторной выборки, только в ней в качестве среднего квадратического отклонения принимается
 ,
,
где σ
1σ2…σk – средние квадратические отклонения в каждой типической группе. Использование средневзвешенного среднего квадратического отклонения (Ошибка серийной выборки рассчитывается по формуле:
![]() ,
,
где δ – среднее квадратическое отклонение для среднего из серий;
S – число всех серий;
S – число отобранных серий.
Знание величины ошибки выборки еще недостаточно, чтобы быть уверенным в результатах выборочного наблюдения, так как конкретная ошибка каждого одного выборочного наблюдения может быть значительно больше (меньше) величины средней оши
бки выборки. Поэтому, кроме величины средней ошибки выборки. На практике следует определять также пределы возможных ошибок выборки. Установлено, что при достаточно большом числе случайно отобранных единиц наблюдений, распределение выборочных средн
их близко к нормальному распределению. П.Л. Чебышев и А.М.Ляпунов нашли численное значение вероятности того, что ошибка выборки не будет выходить за величину заданных (допустимых) пределов. Пределы возможных отклонений выборочных средних (![]() ) от генеральной средней (
) от генеральной средней (![]() ), выраженные в долях
), выраженные в долях
Показатель
t дает возможность определить вероятность правильного ответа, т.е. указывает, что полученная величин а ошибки выборки будет не больше действительной ошибки, допущенной вследствие несплошного характера наблюдения. Так, если принять t =2,6 , то вероятность правильного ответа равна 0,99, т.е. из ста выборочных наблюдений только один раз выборочная средняя окажется вне пределов генеральной средней плюс 2,6 mx. При t = 1 вероятность правильного определения пределов для генеральной средней равна только 0,68 (из 100 выборочных наблюдений 32 средних могут оказаться вне вычисленных пределов).Доверие к такому утверждению измеряется с помощью специального показателя, который называется коэффициентом доверия, или доверительной вероятностью (
Pt). Доверительная вероятность характеризует надежность результатов выборочных медико-статистических исследований (следовательно, надежность результатов выборочного исследования – это вероятность того, что ошибка полученного показателя будет не больше определ енной величины, в практике называемой предельной ошибкой). Обычно в медико-статистических исследованиях используют доверительную вероятность (надежность) 95 или 99 процентов (Pt =0,95 или Pt = 0,99). В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении , используют Pt = 0,997 (99,7%).Предельная ошибка выборочного исследования (Δ
=±tm) позволяет определить величину доверительного интервала, в пред елах которого с определенной вероятностью находится подлинная величина обобщенного показателя.Под характеристикой точности результатов выборочного статистического исследования понимают приближение, с которым получаются подлинные значения исследуемого показателя. Численно величина точности равна ошибке, допускаемой вс ледствие несплошного характера проведенного исследования. Увеличивая доверительную вероятность, мы увеличиваем ширину доверительного интервала, снижая тем самым точность заключения, что в свою очередь повышает уверенность в достоверности суждения.
ГЛАВА V11
ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ
Применение средней ошибки. Задачей статистического исследования является изучение закономерностей, лежащих в самой природе исследуемых явлений. Полученные в резу льтате исследования относительные числа и средние величины должны слудить отображением действительности.
В статистике “интерес нацелен не на те случайные числа. Которые непосредственно устанавливаются подсчетами, а на те истинные величины, которые характеризуют всю массу, познаваемую нами по выборке: состав планктона не в зачерпнутой случайно пробе, а в море, не числа кровяных шариков в поле зрения микроскопа, а свойства крови больного” (А.А.Чупров).
Теория статистики позволяет определить степень достоверности результатов статистического исследования. Поэтому, проводя статистическое исследование, нужно использовать эти возможности для надлежащей оценки полученных данных.
Для определения степени достоверности результатов статистического исследования нужно для каждой относительной или средней величины вычислять соответствующую среднюю ошибку.
Методика расчета средней ошибки (
m) для относительных и средних величин показана в гл.V1.Средняя ошибка позволяет определить пределы, в которых с той или иной степенью вероятности может находиться истинное значение статистического коэффициента или средней величины. Для того, чтобы результаты исчисления соответствовали той степени вероятности, с которой требуется получить нужные выводы, величины
m следует умножить на доверительный коэффициент t , значения которого приведены в табл.30 (см. ниже).Табл.3.0 Краткая таблица значений интеграла вероятностей
|
t |
Pt |
t |
Pt |
t |
Pt |
t |
Pt |
|
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 |
0,0797 0,1585 0,2358 0,3108 0,3829 0,4515 0,5161 0,5763 0,6319 0,6827 |
1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 |
0,7287 0,7699 0,8064 0,8385 0,8664 0,8904 0,9109 0.9281 0,9426 0,9545 |
2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 |
0,9643 0,9722 0,9786 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973 |
3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 |
0,9981 0,9986 0,9990 0,9993 0,9995 0,9997 0,9998 0,9999 0,9999 0,9999 |
Как видно из таблицы 30, вероятность получения правильного заключения возрастает с увеличением
t . Практически достаточно бра ть t, равное 1,96 (2,0) или 2,58 и только в случаях, требующих особенно большой степени вероятности, приравнивать его к 3.Так, например, на основании измерения веса определенного правильно отобранного числа мальчиков одного возраста (8 лет), проживающих в поселке Н, установлено, что средняя арифметическая вел ичина веса у них равна 23,89 кг, а средняя ошибка средней арифметической – 0,14 кг. В таком случае с вероятностью, равной 68,3%, можно утверждать, что средний вес всех мальчиков того же возраста в этом поселке не превышает
28,39±0,14 (Понимать это надлежит следующим образом. если аналогичное исследование будет повторено 100 раз, то лишь примерно в 1 случае из 100 могут быть получены показатели среднего веса, меньше чем 23,54 кг или больше , чем 24,24 кг, а только в 5 случаях из 100 можно ожидать, что средняя величина веса будет меньше чем 23,61 кг или больше, чем 24, 17 кг, и т.д.
Точно так же, если на основе ряда правильно организованных статистических наблюдений установлена эффективность воздействия на больной организм какого-либо лечебного препарата и сделано заключение о достоверности этого вывода с веро ятностью 0,95 (95%), что примерно соответствует
t = 2, то при повторных опытах, организованных таким же образом, как и и первый, вывод об эффективном действии препарата будет подтвержд ен в 95 из 100 случаев.Средняя ошибка разности. При оценке достоверности разности между двумя средними или относительными величинами вычисляется средняя ошибка этой разности по формуле :
![]() ,
,
т.е. средняя ошибка разности равняется квадратному корню из суммы квадратов средних ошибок сравниваемых средних.
Если разность средних величин (относительных коэффициентов) больше средней ошибки разности в 2,5-3,0 или хотя бы в 2 раза, то с вероятностью, определяемой по табл. 30, можно утверждать, что различие средних (относительных) величин не случайно, а зависит от какой-то определенной причины. Ели же разность средних меньше, чем в 2 раза, превышает свою среднюю
ошибку, нет достаточных оснований считать, что различие этих сред них не случайно. При повторных исследованиях это различие может не подтвердиться.В поселке А со 120 000 населения заболело брюшным тифом 256 человек; в поселке Б с 70 000 населения заболело той же болезнью 97 человек. Если возрастно-половой состав населения этих поселков примерно одинаков, то для сравнения разм еров заболеваемости в этих поселках можно использовать обычные интенсивные коэффициенты (на 10 000 населения).
Заболеваемость в поселке А равна ![]() , в поселке Б –
, в поселке Б –
![]() . Требуется решить, является ли преобладание уровня заболе-ваемости в поселке А случай
ным или оно является результатом худшего санитар-но-эпидемиологического состояния этого поселка и требуется принять специаль-ные
меры для его оздоровления. Средние ошибки коэффициентов равны:
. Требуется решить, является ли преобладание уровня заболе-ваемости в поселке А случай
ным или оно является результатом худшего санитар-но-эпидемиологического состояния этого поселка и требуется принять специаль-ные
меры для его оздоровления. Средние ошибки коэффициентов равны:
![]() ,
,
![]() .
.
Средняя ошибка разности коэффициентов:
![]() .
.
Разность коэффициентов равна 21,3-13,9 =7,4. Отношение этой разности к средней ошибке 7,4 : 1,4 >5. Следовательно, разность эта не случайна. В поселке А действительно худшее сан.-эпид. Состояние, чем в поселке Б.
Аналогичнм образом оценивается достоверность различия между средними величинами. Так, например, средний вес 10-летних мальчиков в данном поселке в прошлом году составлял 28,1 кг. В этом году средний вес мальчиков того же воз раста в том же поселке понизился до 28 кг. Есть ли основание считать, что понижение веса не случайно и отражает какое-либо ухудшение в физическом развитии детей?
Вычисленные одновременно со средними величинами средние квадратические отклонения составляли для первой средней величины 3,4 кг, для второй – 3,8 кг. В прошлом году вес измерялся у 600 детей. В данном году – у 700.
Пользуясь формулой для вычисления средней ошибки средних арифметических, приведенной на стр.76, получим :
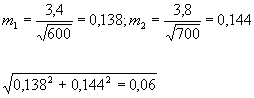
Средняя ошибка разности равна:
Сама разность средних величин равна 28,1-28,0=0,1 и она не превышает даже в 2 раза свою среднюю ошибку. Следовательно, в данном случае небольшое снижение веса детей явл яется случайным и не может считаться показателем ухудшения их физического развития. Если бы разность средних превышала свою среднюю ошибку в 2-3 раза, вывод бы был обратным.
Малые выборки. Привденные выше формулы и построенные на основании их оценочные таблицы применимы только при наличии относительно большого (практически не менее 30) числа наблюдений. При меньшем количестве наблюдений (так называемая малая выб орка), что довольно часто имеет место в клинических и экспериментальных работах, для оценки достоверности результатов прибегают к специальным таблицам. (Напомним, что среднее
квадратическ ое отклонение при малых выборках вычисляется по формуле:![]() ).
).
Это объясняется тем, что при небольших выборках распределение выборочных средних систематически отклоняется от кривой нормального распределения. Большие отклонения от генеральной средней п ри малых выборках являются более вероятными, чем при больших выборках.
Английский ученый В.Госсет (Стьюдент) исследовал распределение
t для малых выборок и установил формулу плотности этого распределения.Для определения пределов колеблемости полученной по данным малдой выборки средней величины и оценки достоверности различий, сравниваемых средних (относительных величин) используют специальную таблицу критерия
t (Стьдента).В графах 2.3 и 4 таблицы помещены величины доверительного коэффициента
(t), показывающие во сколько раз разность сравниваемых величин при данном малом чис ле наблюдений должна превышать свою среднюю ошибку для того, чтобы эта разность могла быть признана достоверной с данным уровнем вероятности, а результаты статистического исследования – достаточно надежными. Числа графы 2-й исчислены для вероятности прав ильного заключения равной 0,95 (95%) и вероятности ошибки – 0,05 (5%), числа графы 3-й – с соответствующими вероятностями 0,99 (99%) и 0,01(1%); числа графы 4-й соответственно – 99,9 и 0,1%. Практически достаточно пользоваться числами графы 3 и даже 2 и только в случае необходимости, особенно большой точности, прибегать к числам графы 4.Значение коэффициента
t (Стьюдента) зависит не только от вероятности (рt), но и от объема выборки (при n` = n-1). Из таблицы видно, что чем меньше выборка, тем больше значение t.Обращаться к таблице следует по графе 1, в которой указано число степеней свободы
n` = n-1, т.е. числу проведенных наб людений , уменьшенному на единицу. Так, например, если после 8 испытаний действия спинномозговой анестезии на уровень кровяного двления установлено, что средняя величина снижения кровяного давления составляла 5,75 мм при средней ошибке 0,65, то из таблиц ы t видно, что при n` = 8-1 = 7; t =2,36 (графа 2 приложения 11). Это значит, что с вероятностью ошибки не более чем 5% можно утверждать, что размеры снижения кровяного давления при спинномозговой анестезии находятся в пределах 5,75±2,36 х 0,65, т.е. в пределах 5,75±1,53 или 4,22 – 8,26 мм; с вероятностью ошибки не более чем 1% можно утверждать, что ра змеры снижения кровяного давления в результате спинномозговой анестезии составляют 5,75±3,50 х 0,65 (графа 3 приложения 11) или 3.48 – 8,02 мм.Если оценивается достоверность разности коэффициентов или средних, т.е.  , то
, то
Среднее падение АД при спинномозговой анестезии ![]() , а при эфирном наркозе
, а при эфирном наркозе ![]() ; случайна ли разность
; случайна ли разность ![]() или действительно эфирный наркоз вызывает меньшее падение АД, чем спинномозговая анестезия?
или действительно эфирный наркоз вызывает меньшее падение АД, чем спинномозговая анестезия?
Таблица 31.
Падение артериального давления в зависимости от вида обезболивани
я|
Вид обезболивания |
Падение артериального давления в мм во время опыта |
|
Спинномозговая анестезия ( v1)Эфирный наркоз ( v2) |
2 3 4 2 7 5 4 3 |
Вычисления
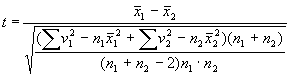 .
.
Упрощение расчетов при использовании этой формулы достигается тем, что вместо вычисления σ и
m для каждогоΣ
v12= 62+52+72+42 +82 +52 =288 , аΣ
v22 = 22 +32 +42 + 22 +72+52 42 +32 =132.![]() как указано было выше, равняются соответственно 5,75 и 3,75; их квадраты
как указано было выше, равняются соответственно 5,75 и 3,75; их квадраты ![]() .
.
Подставив все эти числа в приведенную выше формулу, получим:
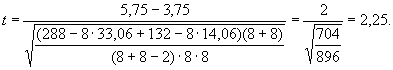
Оценивая
t по данным приложения 2, видим, что при n` =8 +8-2=14 в графе 2 этой таблицы стоит величина 2.14. Следовательно, для достоверности утверждения неслучайности различия величинОценка достоверности интенсивных коэффициентов заболеваемости при наличии повторных заболеваний. Формула средней ошибки показателя
По этой формуле можно исчислять средние ошибки коэффициентов смертности, летальности, а также заболеваемости теми болезнями, которыми, как правило, можно заболеть только один раз (хронические болезни – коронаросклероз, злокачествен ные опухоли, острозаразные заболевания, дающие длительный иммунитет, и т.п.) в течение жизни или хотя бы только один раз за период наблюдения (обычно год).
Определить среднюю ошибку по указанной выше формуле для коэффциентов общей заболеваемости (т.е. заболеваемости всеми болезнями, вместе взятыми) или заболеваемости с временной утратой трудоспособности неправильно.
Практически в течение года человек может болеть несколько раз различными болезнями или даже одной и той же болезнью, длящейся относительно недолго и не дающей стойкого иммунитета (например, грипп, острый катар верхних дыхательных п утей, ангина, пневмония и др.). Случаев временной нетрудоспособности в связи с заболеванием также может быть несколько за год у одного и того же работающего не только в связи с заболеваниями некоторыми острыми болезнями, но и по поводу обострений хрониче ских болезней.
В таких случаях средние ошибки показателей заболеваемости следует рассчитывать по формуле средней ошибки средних величин, т.е.
![]() , строя вариационные ряды, где вариантами являются числа заболеваний или случаев временной нетрудоспособности в связи с заболеванием в течение года (
0;1;2;3;4 и т.д.), а частотами – числа болевших данное число раз.
, строя вариационные ряды, где вариантами являются числа заболеваний или случаев временной нетрудоспособности в связи с заболеванием в течение года (
0;1;2;3;4 и т.д.), а частотами – числа болевших данное число раз.
Однако такие расчеты, правильные теоретически, трудно осуществимы на практике, так как требуют кропотливой работы по распределению наблюдаемой группы населения на не болевших ни разу за год, болевших один раз, два раза и т.д.
Трудность этой работы зачастую заставляет вовсе отказываться от расчета средних ошибок коэффициентов заболеваемости, а следовательно, и от статистической оценки достоверности их разности.
В подобной ситуации допустимо приближенное вычисление средней ошибки показателей, предложенное В.А.Мозгляковой. Исходя из предположения, что распределение по числу заболеваний во многих случаях близко к так называемому распределени ю Пуассона, при котором наибольшие частоты соответствуют не средним, а наименьшим вариантам, В.А.Мозглякова предложила в целях упрощения пользоваться расчетом средних квадратических отклонений и средних ошибок уровней заболеваемости по формулам, пригодны м для распределения Пуассона, а именно:
![]() а
а ![]() .
.
Хорошее соответствие фактического распределения кратности заболеваний теоретическому распределению Пуассона имеет место при числе наблюдений 100-150 и средней величине коэффициента заболев аемости 1,0 на 1 человека. Если коэффициент больше 1.5, то рекомендуемым расчетом не следует пользоваться.
Описанные методы оценки достоверности результатов статистического исследования с помощью критерия
t (критерий Стьюдента) в основном пригодны для так называемого нормального распределения, т.е. такого, при котором крайние значения (самые малые и самые большие) вариант встречаются редко, а наиболее часты варианты. Близкие по своей величине к средней арифметической ряда; или для состояния (да-нет, жив-умер и т.п.). Методы оценки достоверности различия параметров таких вариационных рядов называются параметрическими.Однако характер распределения медико-биологических явлений нередко отличается от нормального. Проводя новые исследования, врач-экспериментатор часто не знает, какому закону варьирования будут следовать результаты, полученные в нескольких опытах, а относительно небольшое число проведенных наблюдений не позволяет ему определить форму распределения. В этих случаях оценку достоверности следует производить с применением так называемых непараметрических критериев.