
Р.М. ХВАСТУНОВ. 1993
УДК
614.71/.73:613.61-07Р.М. Хвастунов
СТАТИСТИЧЕСКИЙ КРИТЕРИЙ ДЛЯ ОБНАРУЖЕНИЯ ВЫПАДАЮЩИХ ЗНАЧЕНИЙ ПОКАЗАТЕЛЕЙ
Московский НИИ гигиены им. Ф.Ф. Эрисмана
Прежде чем вычислять те или иные обобщенные характеристики данных медико-гигиенических исследований (среднее, дисперсию и т.п.), необходимо проверить имеющуюся совокупность данных на наличие выпадающих значений. Выпадающие значения обусловлены либо методическими ошибками в ходе выполнения измерений, либо наличием в изучаемой совокупности объектов, обладающих особыми свойствами, которые резко отличаются от свойств большинства других объектов. В обоих случаях выпадающие значения должны быть обнаружены и принято решение о возможности их дальнейшего использования.
Рекомендуемый в большинстве руководств [2, 4] для этой цели критерий, основанный на предпосылке нормальности распределения данных в анализируемой совокупности, требует выполнения довольно длительных вычислений. Поэтому значительную популярность приобрел критерий отношения интервалов τ, приведенный в работах [1, 3|. Он основан на оценке отклонения значения, подозреваемого на выпадение, от ближайшего к нему значения остальной совокупности. Пусть, например, в ряду значений, расположенных в порядке возрастания, x1, x2, .... xп-1, xn предполагают выпадение значения xn. Тогда составляют отношение:
 (I)
(I)
и сравнивают с критическим значением (см. таблицу, столбцы 2 и 4), Если вычисленное значение
τ больше критического, то проверяемое значение хn считают выпадающим, если же меньшие, то хn считают принадлежащим к основной совокупности.Указанный критерий достаточно удобен в расчетном плане, однако при применении к небольшому числу данных он позволяет обнаружить выпадающие данные практически только тогда, когда это выпадение очевидно без всякого критерия. На рис. 1 показано взаимное расположение точки, находящейся на критической границе по критерию
τ (черные кружки) и остальной совокупности при общем числе данных п=4, 6 и 10, где видно, что значение, признаваемое выпадающим, находится на весьма значительном расстоянии от интервала, занимаемого основной группой, так, что практик-экспериментатор склонен будет исключить это значение, даже не используя критерий τ.Например, если в основной группе получены значения систолического артериального давления (АД) 80, 100 и 120 мм
. рт. ст. (что соответствует условной норме), то минимальное значение, признаваемое выпадающим из этой группы в соответствии с критерием τ, составляет 245. Понятно, что любой врач признает такое значение не относящимся к основной группе и без применения статистического критерия.
Рис. 1. Наиболее близкое к основной группе расположение точек, признаваемых выпадающими в соответствии с критерием т (черные кружки) и предлагаемым критерием λ (светлые кружки).
По горизонтальной оси — расстояние в долях размаха распределения основной группы точек.
Столь большая ширина доверительного интервала (т.е. того интервала, находящаяся в котором точка считается принадлежащей к основной совокупности) неизбежно сопряжена со значительной вероятностью ошибки 2-го рода, т.е. большой вероятностью того, что значение, фактически являющееся выпадающим, будет признано принадлежащим к основной совокупности. Этот недостаток критерия
τ обусловлен тем, что величина размаха R=xn-x1, выборки из генеральной совокупности (в предположении ее нормального распределения) при малых п имеет большую дисперсию [5], в результате чего доверительный интервал для принадлежности точек оказывается очень широким.Указанное обстоятельство побудило нас искать столь же простой в расчетном отношении критерий, что и
τ, однако основанный на других предпосылках, с тем, чтобы выпадение могло быть обнаружено при меньшем относительном отклонении хn от основной совокупности.В качестве исходной модели мы использовали представление о распределении значений внутри интервала, ограниченного минимальным х
1 и максимальным хn из имеющихся значений, исключая сами эти значения (рис. 2). Проверяемая гипотеза H0 состояла в том, что плотность вероятности появлений любого значения xi, внутри [х1, xп] — равномерная. Конкурирующая гипотеза Н1 состояла в том, что интервал постоянной плотности вероятности появления значений хi более короткий: [х1, xn-1] и наблюдаемые значения не могут находиться на интервале от xп-1 до xп. Понятно, что если гипотеза H0 неверна и значения основной совокупности действительно не могут находиться на интервале [xn-1, xп], то и само значение xn не может принадлежать основной совокупности и, следовательно, является выпадающим.
Критические значения τ и λ. для исключения выпадающих значений
при α=0,05 и α
==0,01|
п |
α=0,05 |
α=0,01 |
l1/l2 |
|||
|
τ кр |
λ кр |
τ кр |
λ кр |
α=0,05 |
α=0,01 |
|
|
4 |
0,765 |
0,658 |
0,889 |
0,769 |
0,69 |
0,48 |
|
5 |
0,642 |
0,561 |
0,780 |
0,689 |
0,82 |
0,71 |
|
6 |
0,560 |
0,490 |
0,698 |
0,624 |
0,86 |
0,80 |
|
7 |
0,507 |
0,434 |
0,637 |
0,570 |
0,87 |
0,84 |
|
8 |
0,468 |
0,390 |
0,590 |
0,525 |
0,87 |
0,86 |
|
9 |
0,437 |
0,354 |
0,555 |
0,487 |
0,87 |
0,87 |
|
10 |
0,412 |
0,324 |
0,527 |
0,454 |
0,87 |
0,87 |
|
12 |
0,376 |
0,277 |
0,482 |
0,399 |
0,86 |
0,86 |
|
14 |
0,349 |
0,242 |
0,450 |
0,356 |
0,86 |
0,85 |
|
16 |
0,329 |
0,215 |
0,426 |
0,322 |
0,86 |
0,84 |
|
18 |
0,313 |
0,194 |
0,407 |
0,293 |
0,85 |
0,84 |
|
20 |
0,300 |
0,176 |
0,391 |
0,269 |
0,85 |
0,83 |
|
25 |
0,277 |
0,144 |
0,362 |
0,224 |
0,84 |
0,82 |
|
30 |
0,260 |
0,121 |
0,341 |
0,192 |
0,84 |
0,82 |

Рис. 2. Иллюстрация построения расчетной модели критерия выпадения λ
.x1, x2, … xn-1
— точкн, образующие основную группу, a -— размах распределения этой группы; хn — точка, подозреваемая на выпадение; b — расстояние от крайней точки основной группы до точки, подозреваемой на выпадение.
Для упрощения дальнейших записей обозначим длину интервала
[х1, xn-1] символом a, а длину интервала [xn-1, xп] – символом b.Итак, на интервале а имеется
n—2 значения, а на интервале b значения отсутствуют. В условиях справедливости H0-гипотезы ожидаемые числа значений на интервалах a и b будут: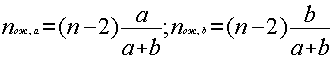
Применим теперь критерий χ
2 для того, чтобы найти такое соотношение длин этих интервалов , при котором различие наблюдаемых частот значений (т.е. чисел п—2 и 0) окажется достоверно не соответствующим гипотезе Н0.
, при котором различие наблюдаемых частот значений (т.е. чисел п—2 и 0) окажется достоверно не соответствующим гипотезе Н0.
Расчет χ
2 в принятой модели следует выполнять по формуле: (3)
(3)
при числе степеней свободы = 1.
Подставив в формулу (3) выражения для
nож, а и nож, b из (2), после элементарных преобразований получаем: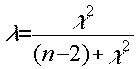 (4)
(4)
Принимая теперь критические значения χ
2 при уровнях значимости α=0,05 и α=0,01 равными 3,84 и 6,64, для различных п получаем критические значения λ (см. таблицу).С помощью данных, приведенных в таблице, легко увидеть, что при фиксированном уровне значимости и любом числе значении п критическое значение λ
меньше, чем критическое значение τ. На рис. 1 для иллюстрации приведены точки (светлые кружки), находящиеся на границе доверительного интервала критерия λ: они расположены гораздо ближе к основной группе, чем граничные точки по критерию τ, и их выпадение не представляется а-priori столь же очевидным.Пример применения критерия
λ. Проведены измерения латентного периода зрительно-моторной реакции (ЗМР) у 10 лиц, осваивающих операторские специальности. Полученные данные расположены в порядке возрастания:Время ЗМР, мс: 11 12 15 20 20 22 25 27 28 39.
Возникает подозрение, что последний результат — выпадающий. Для проверки достоверности выпадения составляем отношение:
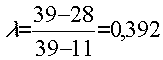
При
n=10 по таблице находим λкр=0,324, что меньше вычисленного λ=0,392. Следовательно, выпадение достоверно.Напротив, по критерию τ критическое значение λкр=0,412 и, следовательно, τ-критерий выпадения не обнаруживает.
Рассмотрим изменение вероятности ошибки 2-го рода (β) в зависимости от расстояния выпадающей точки от
основной группы для предлагаемого критерия λ и критерия τ.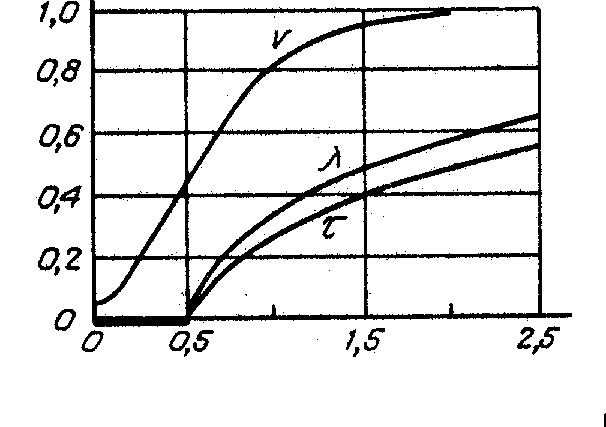
Рис. 3. График функции мощности для односторонних критериев.
Но оси абсцисс — расстояние до подозреваемой на выпадение точки в долях размаха основной группы точек; по оси ординат — вероятность не допустить ошибку 2-го рода. Жирной линией отмечен интервал равномерного распределения (его правая половина) Остальные обозначения в тексте.
Поскольку в условиях Н
1-гипотезы появление замеренного значения в любой точке интервала [х1, xп] предполагается равновероятным, то ошибка 2-го рода будет иметь место, если это значение попадет в интервал [х1, xп-1]. Поэтому вероятность ошибки 2-го рода равна отношению длины интервала [х1, xп-1] к длине интервала [х1, xп] (см. рис. 2):
В работах [1 и 3] не указаны предпосылки, положенные в основу критерия τ, поэтому невозможно непосредственно рассчитать для него значение β. Применим следующий прием: оценим отношение вероятностей ошибок 2-го рода при применении λ
- и τ-критерия. В модели λ-критерия эта величина равна отношению длины интервала [х, λ кр] к длине интервала [х, τ кр] (на рис. 1 для n=4 эти интервалы показаны и обозначены l1 и l2).Значения этого отношения
l1/l2, приведенные в столбцах 6 и 7 таблицы, различны для разных п, но в большинстве близки к 0,85. Таким образом, вероятность ошибки 2-го рода при применении критерия λ приблизительно на 15% меньше, чем при применении традиционного критерия τ.Однако если фактически распределение исходных данных близко к нормальному, то применение предлагаемого критерия сопряжено с большей вероятностью ошибки 2-го рода, чем критерия, основанного на предпосылке нормальности. Действительно, пусть распределение исходных данных (кроме значения, подозреваемого на выпадение) нормально, мы же рассматриваем его как равномерное. Тогда, согласно известному соотношению
R=3,205 σ (γде σ - среднеквадратичное отклонение, а R=xn-1-x1 - размах распределения исходных данных).Допустим, что проверяемая на выпадение точка принадлежит исходному распределению с тем же σ. Пользуясь таблицей функции нормального распределения, находим вероятность ошибки 2-го рода β для различных расстояний проверяемой точки от центра интервала
[х1, xп-1] выраженных в долях R, т.е. для величины z (расстояния проверяемой точки до центра распределения исходных данных в долях его размаха). Так, для значений z 0, 0,2, 0,4, 0,6, 0,8, 1,0, 1,2, 1,4 величины β соответственно равны 0,950, 0,842, 0,642, 0,492, 0,310, 0,161, 0,104, 0,073.На рис. З приведены графики
"функции мощности" Р=1-β, ς.е. вероятности не допустить ошибку 2-го рода в зависимости от величины: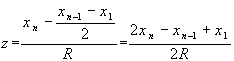
Видно, что предложенный критерий имеет большую мощность, чем критерий τ, но меньшую (если распределение в действительности нормально), чем
V-критерий [4], основанный' на предпосылке нормальности.Предлагаемый критерий обнаружения выпадающих значений λ сочетает простоту расчетов критерия τ с меньшей вероятностью ошибки 2-го рода (большей мощностью). Он может быть применен в тех случаях, когда в силу особенностей происхождения исходных данных распределение значений регистрируемого показателя неотличимо от равномерного.
Предлагаемый критерий может быть применен также и в случае нормального распределения для предварительной оценки возможного выпадения, поэтому если он показывает достоверное выпадение, то проверки по критерию
V не требуется, если же выпадение недостоверно, то возможна более точная проверка по традиционному критерию.
Литература
1.
Ашмарин И. П., Васильев Н. Н., Амбросов В. А. Быстрые методы статистической обработки и планирование экспериментов.— Л., 1971.2.
Каминский Л. С. Статистическая обработка лабораторных и клинических данных.— Л., 1964.3.
Мюллер П.. Пойман П., Шторм Р. Таблицы по математической статистике.— М., 1982.4.
Ноткин Е. Л. Статистика в гигиенических исследованиях.— М„ 1965.5.
Хальд А. Математическая статистика с техническими приложениями.— М., 1956.