Зори А.А., Коренев В.Д., Хламов М.Г. Методы, средства, системы измерения и контроля параметров водных сред. – Донецк: РИА ДонГТУ, 2000.-388 с.
Расчет практической солености
Практическая соленость определяется как функция относительной электрической проводимости при 15 °С (K
15) проб морской воды по отношению к эталонному раствору KCl [63]:![]() , (2.5)
, (2.5)
где K
15 — À (S, 15, 0)/À (КСl, 15, 0); À (S, 15, 0) — удельная электрическая проводимость при 15° С и атмосферном давлении пробы, приготовленной из нормальной морской воды методом разбавления по массе дистиллированной водой или выпариванием; À (КС1, 15, 0) — удельная электрическая проводимость стандартного раствора КСl при 15°С и атмосферном давлении.Следовательно, любые пробы морской воды, имеющие одну и ту же относительную электрическую проводимость RТ, будут иметь одинаковую практическую соленость. Для расчета относительной электрической проводимости RТ при любой температуре [
160] практическая соленость определяется соотношением: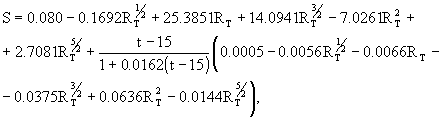 (2.6)
(2.6)
где R
T=À (S, t, 0)/À (35, t, 0); –2£ t£ 35 °С (МПТШ-68); 2£ S£ 42.Для расчета солености, по данным СТД-систем, необходимо учитывать влияние давления на электрическую проводимость R
p=À (S, t, p)/À (S, t, 0). Выражение для Rp, перекрывающее диапазон возможных значений, встречающихся в океанах и морях, находится из соотношения: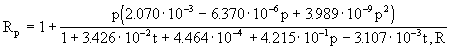 , (2.7)
, (2.7)
где
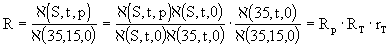 , (2.8)
, (2.8)
где rТ — зависимость относительной электрической проводимости растворов нормальной воды от температуры определяется выражением:
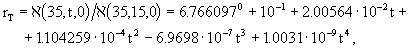 (2.9)
(2.9)
R — относительная электрическая проводимость воды, окружающей преобразователь СТД-системы, с соленостью S, температурой t при давлении Р по отношению к стандартному раствору KCl при 15 °С или эквивалентному ему раствору нормальной морской воды; À
(35, 15, 0)=À (KCl, 15, 0)=42,902 мСм/СМ [63]. По измеряемым значениям относительной электрической проводимости R, давлению Р и температуре t в СТД-системах рассчитываются значения Rp (2.7), rT (2.9), затем из (2.8) — RT. Зная RT, рассчитывается значение практической солености по формуле (2.6).
Международное уравнение состояния морской воды ЮНЕСКО (1980)
В 1980 г. принято Международное уравнение состояния морской воды (МУС-80). Оно определено на основе Шкалы практической солености 1978г. (ШПС-78), является более точным и охватывает большой диапазон температур и давлений. Уравнением состояния морской воды называется зависимость, связывающая между собой параметры состояния — соленость, температуру, давление и плотность.
Относительная плотность морской воды определяется как отношение массы единицы объема воды при той же температуре, которую она имела в момент наблюдений, к массе единицы объема дистиллированной воды при 4°С [
161, 162]. В океанологии принято измерять плотность морской воды в условных единицах (условная плотность):![]() .
.
Условная плотность морской воды обычно составляет от 18 до 32 условных единиц. Для опресненных морей ее значение ниже. Плотность возрастает с увеличением солености и давления. Связь плотности, солености и температуры морской воды при атмосферном давлении представлена на рис. 2.23 по данным
[163]. Зависимость плотности морской воды от давления для S=35 0/00 при различных температурах представлена на рис. 2.24 [162].Плотность r (кг/м
3) морской воды в функции практической солености S, температуры t (°С), приложенного давления (МПа) определяется выражением [159]:![]() , (2.10)
, (2.10)
где K(S, t, p) — средний модуль упругости, Р=0 соответствует одной стандартной атмосфере (101325 Па).
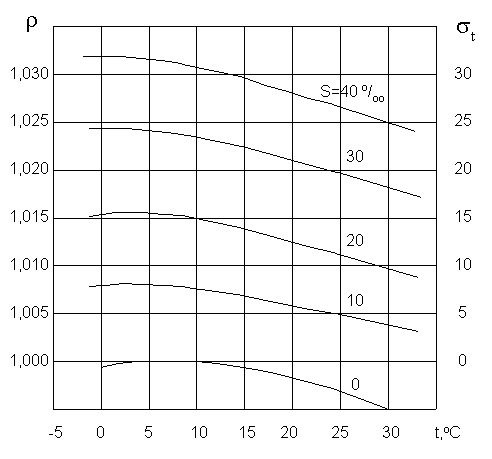
Рисунок 2.23 — Связь плотности морской воды с ее соленостью и
температурой
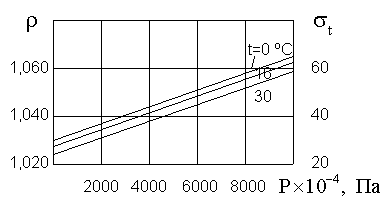
Рисунок 2.24 — Зависимость плотности морской воды
(S=35 0/00) от давленияпри различных температурах
Плотность морской воды при атмосферном давлении (Р=0) может быть определена по соотношению:
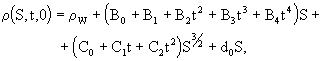 (2.11)
(2.11)
где r
W — плотность стандартной среднеокеанической чистой воды, которая определяется соотношением, рекомендованным международным союзом чистой и прикладной химии [164]:![]() (2.12)
(2.12)
Средний модуль упругости морской воды определяется выражением:
![]() (2.13)
(2.13)
где
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
Численные значения коэффициентов уравнений (2.10—2.19) приведены в [63,
162].Расчет производных (вторичных) гидрологических параметров основан на зависимости их от температуры t, удельной электрической проводимости
Как показано в [63], для расчета вторичных параметров Y
i (соленость, плотность, глубина и др.) с наибольшей точностью в качестве трех первичных параметров целесообразно принять температуру, давление и удельную электрическую проводимость. При этом![]()
При погрешностях лучших измерителей температуры, давления, удельной относительной электрической проводимости: Y
t=0,005 °С, Y À =0,005 мСм/см, Y R=12× 10–5, Y p=1× 10–2 МПа, погрешность расчета солености по выражению (2.5) составляет 0,00870/00.Расчет плотности в функции относительной электрической проводимости, температуры и давления может быть получен аналогично с выражениями (2.11—2.19), (2.6—2.9). Упрощенные формулы для вычисления абсолютной плотности и ее аномалий приведены в [63].
Полиномы для расчетов солености и плотности на микро-ЭВМ в реальном масштабе времени
Современное состояние гидрофизических исследований требует оперативного (в процессе эксперимента) получения вторичных параметров, что позволяет оптимизировать эксперимент, уменьшить избыточность и повысить качество информации.
Международное уравнение состояния морской воды МУС-80 и ШПС-78 практически не могут быть использованы в программном обеспечении СТД-систем на базе микропроцессоров и микро-ЭВМ, в силу сложности реализации дробных степеней переменных, большого количества расчетных формул и коэффициентов. Это усложняет вычисление, требует больших объемов постоянной и оперативной памяти и приводит к большим затратам времени при вычислениях вторичных параметров in situ. В связи с этим возникает необходимость аппроксимации ШПС и МУС степенными многочленами, удобными для реализации на конкретных микропроцессорах и микро-ЭВМ. Порядок степени многочлена должен определяться с учетом погрешностей первичных средств измерения.
Один из разработанных вариантов аппроксимирующих функций S(R, t, p) и s
t(R, t, p) описан в [165] и имеет вид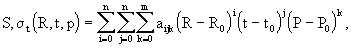 (2.20)
(2.20)
где R
0, t0, P0 — постоянные величины.Аппроксимация проводилась для диапазонов R=0,6–l,6, t=0–30 ° С, Р=0–10 МПа в диапазоне солености 30–40
0/00. Параметры R0, t0 и P0 приняты соответственно 1,1; 15 °С; 0 МПа. Коэффициенты аijk определялись методом наименьших квадратов для многочленов 2-й, 3-й и 4-й степеней. В качестве “точных” величин солености и плотности приняты их значения, вычисленные по МУС-80 и ШПС-78.В работе приведены численные значения коэффициентов многочленов, величины среднеквадратичных и максимальных значений погрешностей вычислений солености и плотности. Расчеты показали, что среднеквадратическое отклонение (СКО) для аппроксимирующих многочленов 2-й степени по отношению к точным значениям составляют ~0,15
0/00 и 0,13 кг/м3 по солености и плотности соответственно. Многочлены 3-й степени обеспечивают ~0,020/00 и 0,02 кг/м3, а 4-й ~0,0070/00 и 0,009 кг/м3 в диапазоне изменения давления Р=0–5 МПа.Оценим выбор порядка полинома с учетом погрешностей первичных средств измерений. Для зонда “Исток-5”, являющегося одним из лучших отечественных приборов, среднеквадратичная погрешность косвенных измерений солености, определенная по ШПС-78, составляет 0,
042% [58]. Использование предлагаемого многочлена 4-й степени вместо ШПС снижает точность вычисления солености (с учетом максимальной погрешности вычислений 0,033%) — до 0,046%, однако при этом скорость вычислений существенно возрастает. Для менее точных средств измерений, а также при косвенных измерениях пульсационных составляющих вторичных параметров достаточную точность могут обеспечить полиномы 3-го, 2-го и даже 1-го порядков. Коэффициенты аппроксимации были также вычислены для вод низкой солености (17—230/00), соответствующих водам Черного моря.Аппроксимация многочленами вида
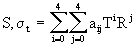 (2.21)
(2.21)
при условии i+j£ 4 для широкого диапазона солености S =5–40
0/00 предложена в [166], обеспечивает СКО 0,0070/00 и 0,008 кг/м3 по плотности.Сравнение шкалы практической солености с другими известными используемыми методами определения солености с помощью аппроксимирующих полиномов показывает, что даже в океаническом диапазоне солености 30–40
0/00 имеют место существенные расхождения, достигающие 0,0340/00 [63]. Кроме того, эти полиномы имеют различную структуру, многоступенчатую последовательность расчета, громоздки. Даже наиболее простой из них метод Парамонова-Калашникова представляет собой полином 4-го порядка с двухступенчатой последовательностью расчета, что усложняет его реализацию на микропроцессорах по сравнению с полиномами вида (2.20, 2.21).Использующиеся на практике методы расчета плотности, анализ и количественная оценка которых приведена в [63], имеют недостатки, характерные для методов расчета солености. Кроме того, в выражение для расчета плотности входит соленость, что значительно снижает возможность его применения в реальном масштабе времени. Предлагаемый МГИ НАН Украины [
167] метод расчета плотности удобен тем, что в нем используется температура, электрическая проводимость и давление. Однако он требует многоступенчатую последовательность расчета и трудно реализуем на микро-ЭВМ.Из проведенного анализа следует, что наиболее приемлемыми для оперативного расчета вторичных параметров СТД-зондов на микропроцессорах и микро-ЭВМ являются полиномы вида (2.20, 2.21). Они универсальны, т. к. имеют одинаковые выражения для расчета всех вторичных параметров: солености S, условной плотности s
t, скорости распространения звука С, оптического показателя преломления n и др. Их применение позволяет унифицировать программное обеспечение микропроцессоров и микро-ЭВМ и снизить затраты времени на его разработку.