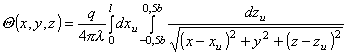Back

 

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НА ВЕРШИНЕ ЛЕЗВИЯ РЕЖУЩЕГО

ИНСТРУМЕНТА С ИСПОЛЬЗОВАНИЕМ МЕТОДА ИСТОЧНИКОВ

 

Ивченко Т.Г., Легащева Т.А. (каф. ТМ, ДонГТУ, г. Донецк, Украина)

 

Тепловые явления при резании оказывают существенное влияние, как на работоспособность режущего инструмента, так и на качество поверхностей обработанных деталей. Экспериментальные методы определения температур при резании весьма трудоемки, в связи с чем, в настоящее время все большее значение приобретают теоретические методы исследования, позволяющие рассчитывать уровень температур в любых точках тел, участвующих в теплообмене. Представленная работа посвящена определению температуры на вершине лезвия инструмента в зависимости от различных параметров механообработки.

В технологической теплофизике для решения тепловых задач наиболее часто применяют метод источников теплоты [1]. С помощью метода источников, основанного на использовании принципов конструирования решений и принципов отражения источников, сравнительно просто можно определить интеграл, удовлетворяющий дифференциальному уравнению теплопроводности и условиям однозначности: дальнейшей задачей является лишь вычисление этого интеграла.

В соответствии с принципом конструирования решений сложные источники представляют в виде той или иной системы, состоящей из мгновенных точечных источников теплоты. Поэтому и температурное поле, возникающее под действием источника сложной формы, получают методом суперпозиции полей, возникающих под действием каждого из мгновенных точечных источников. Математическое выражение, описывающее температурное поле, которое возникает под действием мгновенного точечного источника, имеет вид

 

где Q - количество теплоты, внесенной в тело источником; t -время, прошедшее от момента теплового импульса; λ и ω тепло физические характеристики материала;

 

R - расстояние от места вспышки J(х_и, у_и, z_и)до какой-либо точки тела М(х, у, z).

Источник теплоты, возникающий на передней поверхности лезвия инструмента является плоским двумерным прямоугольным с размерами bхl равным площадке контакта стружки с передней поверхностью [1]. Длина контактной площадки в направлении схода стружки l и ее размер вдоль главной режущей кромки b равны

 

где а - толщина среза, k - коэффициент продольной усадки стружки, g - передний угол резца, s – подача, t - глубина резания, j- главный угол в плане.

Плотность равномерно распределенного теплового потока, действующего в зоне трения стружки о переднюю поверхность инструмента [2].

 

где P_Z0 = P_z – F_тр - разность тангенциальной силы резания и силы трения по задней поверхности лезвия; P_N0= P_y – F_тр - разность нормальной составляющей силы резания и силы трения по передней поверхности лезвия, v - скорость резания [3].

Для того, чтобы описать с помощью формулы (1) температурное поле, возникающие под действием двумерного прямоугольного источника теплоты, равномерно распределенного по площадке bxl необходимо выполнить два интегральных перехода: 1) от точечного источника к двумерному; 2) от мгновенного источника к действующему непрерывно. В результате этих переходов при установившемся теплообмене получено выражение

 

Полученная формула позволяет рассчитать температурное поле на передней поверхности лезвия, считая y=0, а также температуру на вершине лезвия, считая x=0, y=0, z=0. Формулу (5) целесообразно представить в следующем виде

где Т(ψ, ζ) – закон распределения температур в безразмерном виде, ψ = x/l; ζ = z/l – безразмерные координаты.

Значение функции Т(ψ, ζ) в точках ψ = 0; ζ = 0, соответствующих координатам вершины резца, то есть значение Т(0,0) определяется следующим образом 

 

где h - безразмерная величина, равная

Температура на вершине резца при установившемся теплообмене равна

 

где l - коэффициент теплопроводности материала резца.

В соответствии с принципом отражения источников, для того чтобы учесть ограниченность твердых тел, надо выполнить отражение источников теплоты, мысленно прикладывая к основному (реальному) телу ряд подобных ему тел с фиктивными источниками теплоты, при чем каждое из последующих тел должно являться зеркальным отражением предыдущего тела относительно плоскости их соприкосновения.

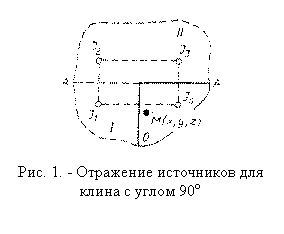Рассмотрим в качестве примера бесконечный клин с углом β=90°  при граничных условиях второго рода q_s= 0. Чтобы перейти к неограниченному телу, нужно: вначале дополнить мысленно клин 0 отраженным клином 1 с фиктивным источником J₁ и получить полупространство: затем дополнить полупространство с источниками J₀ и J₁ полупространством II с фиктивными источниками J₂ и J₃ расположенными симметрично источникам J₀ и J₁ относительно плоскости АА.

Температура в любой точке М основного клина 

(9)

Полученные формулы (4), (9) позволяют определить температуру на вершине сборного резца с механическим креплением квадратной пластины, имеющей угол при вершине 90°. Указанные расчеты реализованы с использованием пакета Mathcad 2000 PROFESSIONAL.

Пример расчета выполнен для следующих исходных данных: обрабатываемый материал - сталь45, предел прочности s=750 МПа, коэффициент усадки стружки  k=2,2;  геометрические параметры токарного резца из твердого сплава Т15К6: углы в плане f=f1=45°, передний угол g=-5°, задний угол a = 5°; режимы резания: глубина  t=2мм; подача s=0,2мм/об;  скорость резания v=150м/мин; износ по задней поверхности h=0,5мм; коэффициент теплопроводности резца l=27,2 Вт/м°С. В результате расчета установлена температура на вершине 280°С.

На основании разработанной методики выполнен анализ влияния различных факторов на температуру резца. Предложенные аналитические зависимости позволяют установить характер и степень влияния свойств обрабатываемого и инструментального материалов, геометрических параметров лезвия инструмента, режимов обработки на температуру вершины лезвия. Указанные параметры оказывают весьма сложное влияние на температуру, так как по-разному влияют на величину теплового потока, возникающего в зоне обработки и размеры площадки контакта стружки с передней поверхностью лезвия.

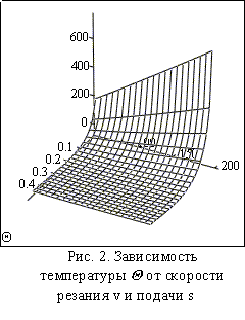На рис. 2 представлена двухпараметрическая зависимость температуры Q на вершине резца от скорости резания в диапазоне ее изменения до 200м/мин и подачи в диапазоне изменения до 0,4 мм/об. Увеличение подачи, как следует из представленного графика, приводит к снижению температуры на вершине резца, так как с ростом подачи (согласно формулам (3) и(4)) увеличивается длина контакта стружки с передней поверхностью l, а, следовательно, снижается плотность теплового потока q. С увеличением же скорости резания плотность теплового потока прямопропорционально увеличивается, что приводит к увеличению температуры.

Таким, образом, в представленной работе разработана методика определения температуры на вершине лезвия инструментов с учетом условий механообработки: свойств обрабатываемого и инструментального материалов, геометрических параметров лезвия инструмента, режимов обработки. С использованием пакета Mathcad 2000 PROFESSIONAL выполнен анализ влияния различных факторов на температуру и на основании выполненных расчетов даны рекомендации по рациональному выбору режимов обработки и параметров инструмента.

 

Список литературы: 1. Резников А.Н. Теплофизика процессов механической обработки материалов. - М.: Машиностроение, 1981. - 279с. 2 .Ивченко Т.Г., Легащева Т.А. Исследование температурного поля резцов, оснащенных минералокерамикой. Прогрессивные технологии и системы машиностроения: Международный сб. научных трудов. – Донецк: ДонГТУ, 2000. Вып. 10. С.81-86. 3. Ивченко Т.Г., Сагуленко Н.Г., Саенко В.В. Определение температурного поля резца с использованием метода конечных разностей //  Прогрессивные технологии и системы машиностроения. - Донецк: ДонГТУ.- 1998.- Вып.5 - С.58-63.