Back

ОБЕСПЕЧЕНИЕ ОПТИМАЛЬНОГО УРОВНЯ

ГАММА-ПРОЦЕНТНОГО ПЕРИОДА СТОЙКОСТИ

ПРИ ЭКСПЛУАТАЦИИ РЕЖУЩЕГО ИНСТРУМЕНТА

Ивченко Т.Г. ( ДонГТУ, г. Донецк, Украина)

Эффективность функционирования современных технологических систем в значительной степени определяется их надежностью. В условиях автоматизированного производства, предъявляющего повышенные требования к надежности режущих инструментов, весьма важным является гарантированное обеспечение показателей безотказности их функционирования, так как случайные отказы приводят к внеплановым простоям дорогостоящего оборудования и значительному увеличению затрат на его обслуживание.

При оценке надежности по средним показателям безотказности, долговечности и ремонтопригодности обеспечивается довольно низкий уровень вероятности, их гарантирующий, не превышающий 0,5. Для условий эксплуатации режущего инструмента в автоматических линиях, на автоматах и полуавтоматах, на станках с числовым программным управлением, представляет интерес исследование в качестве показателей надежности не только их средних значений, но и значений показателей с любым заданным уровнем вероятности.

В настоящей работе наряду с общепринятым показателем безотказности режущего инструмента - средним периодм стойкости, рассматриваются дополнительно следующие показатели: гамма-процентный период стойкости - время резания режущего инструмента, в течение которого он не достигнет отказа с заданной вероятностью g, выраженной в процентах, а также относительный гамма-процентный период стойкости - отношение гамма-процентного периода стойкости к среднему периоду стойкости режущего инструмента.

Для закона Вейбулла-Гнеденко, наиболее распространенного при анализе стойкости режущего инструмента, вероятность безотказной работы, или интегральная функция распределения стойкости P(t), а также плотность распределения, или дифференциальная функция распределения стойкости f(t),  имеют вид:

,

,

где  - параметры масштаба и формы закона распределения.

Средний период стойкости Т и дисперсия D определяются следующим образом:

,

,

где  - гамма-функция.

Коэффициент вариации стойкости, представляющий отношение среднеквадратического отклонения к математическому ожиданию, не зависит от параметра масштаба  и, следовательно, является наиболее удобной характеристикой рассеивания стойкости инструмента:

.

Гамма-процентный период стойкости, или стойкость с заданной вероятностью , определяется следующим образом:

.

Относительный гамма-процентный период стойкости равен:

Для рассмотренного закона Вейбулла-Гнеденко гамма-процент может быть рассчитан следующим образом:

Значения гамма-процента, гарантирующие средний период стойкости, в зависимости от параметра  и соответствующего коэффициента вариации  следующие:

при  = 1 и = 1,000: =36,79%;

при  = 2 и = 0,523: =39,01%;

при  = 3 и = 0,366: =38,17%.

при  = 4 и = 0,366: =37,71%.

Рассчитанные значения свидетельствуют о достаточно низком уровне вероятности, с которой гарантируется средний период стойкости Обеспечение более высокого уровня вероятности при фиксированном качестве инструмента может быть достигнуто за счет уменьшения режимов резания, то есть связано с неизбежным снижением производительности обработки. Коэффициент снижения производительности, характеризующий изменение скорости резания, необходимое для обеспечения заданной гамма-процентной стойкости режущего инструмента, может быть определен следующим образом:

,

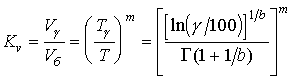где V_б - базовое значение скорости резания, соответствующее среднему периоду стойкости, m - показатель относительной стойкости, характеризующий связь скорости резания со стойкостью инструмента (принимается m=0,2). Влияние гамма-прцента на коэффициент производительности обработки при различных значениях параметра b представлено на рис. 1  

Представленные зависимости свидетельствуют о необходимости существенного снижения производительности для обеспечения требуемого гамма-процента при значительном рассеивании стойкости (V =1, b=1). Снижение рассеивания стойкости, то есть уменьшение коэффициента вариации V и увеличение параметра b, позволяет достигать требуемого гамма-процента при более высокой производительности.

Однако, наряду со снижением производительности имеет место и снижение затрат на эксплуатацию инструмента, связанное с повышением надежности и уменьшением количества отказов инструмента. В связи с этим представляет интерес поиск оптимальных значений гамма-процентного периода стойкости и оптимального гамма-процента, обеспечивающих максимально возможное соотношение производительности обработки и затрат на эксплуатацию инструмента.

В качестве критерия оптимальности целесообразно использовать относительный интегральный показатель [1], в котором затраты на создание инструмента являются постоянными, а снижение затрат на эксплуатацию инструмента З_э в сравнении с базовыми затратами З_эб принимается пропорциональными  относительному гамма-процентному периоду стойкости

,

где - A, n - коэффициент пропорциональности  и показатель степени , характеризующие связь затрат на эксплуатацию инструмента с. относительным гамма-процентным периодом стойкости

Относительный интегральный показатель качества  в зависимости от показателя безотказности рассматривается при условии постоянства остальных показателей надежности - ремонтопригодности и долговечности, которые для дальнейших расчетов принимаются равными их базовым значениям. В этом случае критерий оптимальности имеет вид:

. ,

где- C  - постоянный коэффициент, характеризующий затраты на создание режущего инструмента:     - стоимость инструмента,  -  затраты , приходящиеся на 1 минуту работы инструмента и станка, К-  среднее число периодов стойкости.

Графики критерия оптимальности K(X) в зависимости от параметра оптимизации - относительного гамма-процентного периода стойкости X при значениях m = 0,2,   n = 2 для различных значений  C 

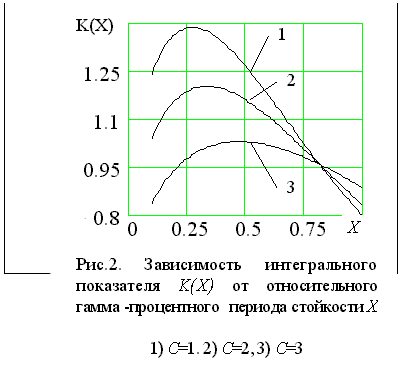
Анализ представленных результатов свидетельствует об экстремальном характере интегрального показателя с использованием в качестве отдельных показателей безотказности их значений с любым заданным уровнем вероятности g в сравнении с принятым за базовый интегральным показателем, рассчитанным по средним значениям. С увеличением параметра С экстремум сдвигается в сторону больших значений.

Оптимальные значения показателей безотказности с заданным уровнем вероятности g - оптимальный относительный гамма-процентный период стойкости и оптимальный гамма-процент, обеспечивающие максимальное значение критерия оптимальности - интегрального показателя, определяются следующим образом:

,

.

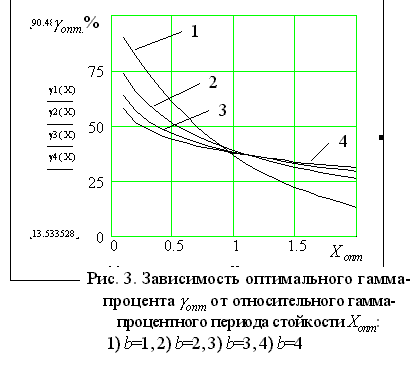
зависимость оптимального гамма-процента от относительного гамма-процентного периода стойкости X _опт  для различных  значений параметра b закона распределения стойкости режущего инструмента представлена на рис.3  

В результате проведенных исследований выявлены факторы, определяющие оптимальные значения показателей безотказности с вероятностью g. Установлено, что оптимальный гамма процент зависит от параметра b закона распределения, то есть от рассеивания стойкости режущего инструмента. При одном и том же X_опт для X_опт<1 оптимальный гамма-процент тем выше, чем больше рассеивание стойкости, то есть больше  коэффициент вариации (V =1, b=1).

Таким образом, разработана методика определения оптимальных значения показателей безотказности с вероятностью g, обеспечивающих максимальное значение  интегрального показателя качества, то есть максимально возможное соотношение производительности обработки и затрат на эксплуатацию режущего инструмента.

Back