Back

ВЕРОЯТНОСТНЫЙ ПОДХОД К ОЦЕНКЕ ПРОЧНОСТИ ДЕТАЛЕЙ МАШИН

Ивченко Т. Г., Легащева Т.А., Сытник М.Н.

(ДонГТУ, г. Донецк, Украина)

    В современных сложных технических системах отказ даже одного элемента может привести к серьезным последствиям. Поэтому весьма важной задачей инженера – конструктора является оценивание надежности элементов, определяемой, прежде всего, их прочностью, на этапе проектирования. Повышение требований к качеству изделий машиностроения подтверждает актуальность этой задачи и для деталей машин.

    Общепринятый детерминистский подход к оценке прочности, основанный на расчете коэффициентов безопасности и запаса прочности, не позволяет судить о вероятности отказа элемента. Случайный характер действующих нагрузок, рассеивание конструктивных параметров и физико-механических свойств деталей машин обуславливают целесообразность использования вероятностных прочностных расчетов.

    Сущность вероятностного подхода к оценке прочности заключается в определении вероятности отказа детали на основании сопоставления значений напряжения и прочности с учетом законов их распределений. Отказ наступает, если фактически действующие напряжения превышают предел прочности, вероятность отказа при этом равна [1]:

    где F_P(s), f_P(s) - интегральная и дифференциальная функции распределения прочности детали; F_S(s), f_S(s) - функции распределения напряжения.

Для нормального закона распределения показателей прочности и напряжения, наиболее распространенных для деталей машин, вероятность отказа может быть определена следующим образом:

    где F(z) – нормированная функция Лапласса; V_P = s_Р/m_P, V_S = s_S/m_S - коэффициенты вариации показателей прочности и напряжения: s_Р и s_S среднеквадратические отклонения, m_P и m_S средние значения показателей прочности и напряжения соответственно; h = m_P/m_S  - коэффициент безопасности.

    Влияние коэффициента безопасности h на вероятность отказа Р при различных значениях коэффициента вариации V (принято V_P = V_S) представлено на рис.1

Полученное выражение позволяет оценивать вероятность отказа по коэффициенту безопасности, причем, чем больше коэффициент вариации, то есть, чем выше рассеивание прочности и напряжения, тем выше при одном и том же значении коэффициента безопасности вероятность отказа. При известном значении коэффициента вариации может быть определено значение коэффициента безопасности, обеспечивающее заданное значение вероятности отказа.

    В качестве примера рассмотрены расчеты на растяжение и кручение элемента, имеющего круговое поперечное сечение. Вследствие производственных допусков его диаметр d является случайной величиной со среднеквадратическим отклонением s_r. Если допуск для радиуса кругового поперечного сечения равен некоторой доле a радиуса, то 3s_r = a r, следовательно, s_r = (a /3)r. Задана требуемая вероятность безотказной работы элемента R.

    Растягивающая нагрузка Н и крутящий момент Т, действующие на элемент, являются случайными величинами со среднеквадратическими отклонениями s_Н и s_Т. Предел прочности на растяжение S_Н и допустимое напряжение среза S_Т материала, используемого для изготовления этого элемента, также являются случайными величинами со среднеквадратическими отклонениями s_SН и s_SТ.

    Растягивающее напряжение равно s = Н/A = Н/p r², где A=p r² - площадь сечения Напряжение среза t = Тd/2I_P = 2Т/p r³, где I_P = p d⁴/32 – момент инерции сечения. Очевидно, что напряжения являются функцией двух случайных аргументов – нагрузки и радиуса кругового сечения.

    Математическое ожидание и дисперсия функции n случайных аргументов f(x₁,x₂, , x_n) определяется на основании разложения в ряд Тейлора следующим образом:

    где m_i, s ²(x_i) – , s ²(x_i) – математические ожидания и дисперсии случайных аргументов.

    Растягивающее напряжение и напряжение среза с их среднеквадратическими отклонениями рассчитываются по заданной нагрузке и размерам сечения учетом разложения в ряд Тейлора (3):

    Для определения заданного уровня вероятности безотказной работы элемента, работающего на растяжение и кручение, используются следующие выражения:

    Полученные выражения позволяет рассчитывать размеры кругового поперечного сечения элемента, обеспечивающие заданный уровень его безотказности при действии растягивающей и скручивающей нагрузки.

    Расчеты на растяжение выполнены для следующих условий: Н = 17800Н, s_Н = 445Н, S_Н = 690Мпа, s_SН.= 34,5Мпа, a = 0,015, R = 0,99990.

    При заданной вероятности безотказной работы R = 0,99990 значение аргумента нормированной функции Лапласса z = -3,72. После выполнения расчетов получаем уравнение для определения r:

144,63 r⁴ – 24,6 r² +1 = 0;

    откуда определяется положительный корень r = 3,21мм, соответствующий заданной вероятности безотказной работы.

    Расчеты на кручение выполнены для следующих условий: Т = 11300Нм, s _Т = 1130Нм, S_T = 345Мпа, s_ST.=34,5Мпа, a = 0,03, R = 0,99900.

    При заданной вероятности безотказной работы R = 0,99900 значение аргумента нормированной функции Лапласса z = -3,07. После выполнения расчетов получаем уравнение для определения r:

r⁶ – 46,1056 r³ +0.8666 = 0;

    откуда определяется положительный корень r = 32,13мм, соответствующий заданной вероятности безотказной работы.

    Таким образом, вероятностный подход к оценке прочности деталей машин позволяет уже на стадии проектирования прогнозировать вероятность их отказа, а также обеспечивать требуемый уровень вероятности безотказной работы за счет выбора рациональных параметров.

Список литературы: 1. Капур К., Ламберсон Л. Надежность и проектирование систем. М.: Мир, 1980. – 606с.
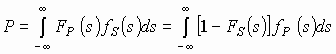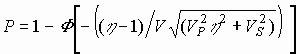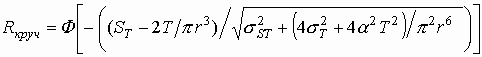