Naumov O. E., Larin A.M. Frequency computation method of transitional processes in synchronous generators attached to asymmetrical short-circuits. In given article is offered a computation method of transitional processes in generators attached to asymmetrical short-circuit in system, founded on use of frequency descriptions of synchronous engines. For two-phase and two-phase on earth short-circuits from routine of single motion is shown stator currents computation principle and electromagnetic revolving moment. In detail is considered decomposition stator currents on symmetric constituents.

При частотном методе расчета переходных процессов величины токов КЗ находятся с помощью частотных характеристик синхронных машин. Достоинствами данного метода являются простота (не требуется решать систему дифференциальных уравнений синхронной машины), наглядность, легкость учета внешних сопротивлений.

В работе [1] показано, что при несимметричных КЗ как в обмотке статора, так и в обмотке ротора возникает полный спектр высших гармоник. В свою очередь, каждая гармоника в соответствии с методом симметричных составляющих может быть представлена в виде суммы токов прямой, обратной и, если есть замыкание на землю, нулевой последовательностей. В практических расчетах, однако, высшими гармониками можно пренебречь, особенно в машинах с демпферными обмотками. В этом случае расчет ведется только для первой гармоники.

Частотная характеристика синхронной машины, как известно, представляет собой зависимость комплекса тока статора от скольжения ротора. Поскольку ротор несимметричен в магнитном и электрическом отношении то машина характеризуется двумя частотными характеристиками: по оси d - Y_d(js), по оси q - Y_qjs). Иногда для упрощения расчетов их заменяют эквивалентной характеристикой, одинаковой для осей d и q. Следует обратить внимание на то, что найденный по частотной характеристике ток статора - это фактически ток включения машины на какое-либо напряжение. Поэтому для того, чтобы найти ток короткого замыкания (как симметричного трехфазного, так и несимметричного), необходимо представить процесс короткого замыкания как процесс включения синхронной машины на некоторое напряжение. Так, трехфазное КЗ можно представить как включение на трехфазную систему напряжений, равных по величине и противоположных по направлению тем фазным напряжениям, которые были до замыкания; однофазное КЗ фазы A – включением машины на напряжение -E_a и т.д. Более подробное рассмотрение этого вопроса приведено в [2]. Однако в данной работе впервые применен несколько другой подход, а именно: рассмотрение несимметричных КЗ как включение машины на напряжения прямой и обратной последовательностей, то есть симметричные составляющие.

Рассмотрим определение составляющих токов КЗ статора по частотным характеристикам на примере двухфазного КЗ. Предположим, что замыкание фаз B и C производится из режима холостого хода. Согласно методу симметричных составляющих фазные напряжения машины можно представить как сумму трехфазных симметричных систем напряжений прямой (U_a1, U_b1, U_c1) и обратной (U_a2, U_b2, U_c2) последовательностей. Изображающий вектор напряжения прямой последовательности будет вращаться с синхронной скоростью в направлении движения ротора, а вектор обратной последовательности – также с синхронной скоростью, но в обратном направлении. Под действием этих напряжений в фазах статора появятся токи прямой и обратной последовательностей.

Ток прямой последовательности можно разложить на три составляющие: периодический установившийся, апериодический и периодический переходные токи. Примем допущение, что синхронная машина характеризуется одной усредненной для осей d и q частотной характеристикой, а изменение скольжения настолько мало, что им можно пренебречь. Тогда периодический установившийся ток прямой последовательности будет представлен вектором, соединяющим начало координат и точку s = 0 частотной характеристики. В системе неподвижных координатных осей этот вектор вращается с синхронной скоростью в направлении вращения ротора. Апериодический переходный ток отражается вектором, который в начальный момент времени соединяет начало координат и точку s = -1 частотной характеристики. В дальнейшем этот вектор останется практически неподвижным относительно статора, а ток будет затухать с постоянной времени T_a (для трехфазного и двухфазного КЗ величины T_aпримерно равны). Начальное значение периодического переходного тока может быть найдено из условия:

где I₁₁(0), I₂₁(0) и I₀₁(0) - величины соответственно апериодического, периодического переходного и установившегося токов при t = 0. Это условие вытекает из первого закона коммутации: если до КЗ генератор работал в режиме холостого хода и ток статора равнялся нулю, то и в первый момент после коммутации он должен оставаться равным нулю. Периодический переходный ток рассчитывается как сумма составляющих по осям d и q, количество и величина которых зависят от количества роторных контуров в схеме замещения синхронной машины и их параметров. Вектор этого тока, вращаясь с синхронной скоростью в положительном направлении, будет затухать с постоянными времени, определяемыми параметрами роторных контуров.

Аналогичное разложение проводится для токов обратной последовательности. В этом случае вектор установившегося тока I₀₂(t) будет вращаться с синхронной скоростью в направлении, обратном направлению вращения ротора, т.е. будет иметь относительно него скольжение -2. Соответственно на частотной характеристике он будет соединять начало координат и точку s = -2 характеристики. Величина и характер затухания апериодической составляющей I₂₁(t) будут такими же, как и для прямой последовательности. Величина начального значения периодического переходного тока определяется из условия, подобного (1):

Поэтому вектор этого тока при t = 0 будет соединять точки s = -1 и s = -2 частотной характеристики. В дальнейшем он будет вращаться со скольжением -2 относительно ротора и затухать с постоянными времени роторных контуров, вычисленных для обратной последовательности.

Просуммировав составляющие токов прямой и обратной последовательностей, получим изображающие векторы тока статора I_s1(t) и I_s2(t) соответственно. Фазные токи синхронного генератора находятся как сумма проекций I_s1(t) и I_s2(t) на соответствующие оси. Для двухфазного КЗ эта сумма в фазе А должна быть равна нулю в любой момент времени.

При однофазном КЗ и двухфазном КЗ на землю, кроме вышеупомянутых прямой и обратной последовательностей, появляется еще и нулевая последовательность. В этом случае к изображающим векторам ПП и ОП следует прибавить вектор тока нулевой последовательности:

где U₀ – величина напряжения нулевой последовательности, X₀ – сопротивление НП синхронного генератора. Проекции этого вектора на фазные оси дадут составляющие нулевой последовательности фазных токов.

Для проверки данного метода был произведен расчет двухфазного КЗ синхронного генератора Т-4376/142 Зуевской ГРЭС. На этом генераторе производились опыты гашения поля, симметричного (трехфазного) и несимметричного (двухфазного) коротких замыканий, получены осциллограммы фазных токов статора, тока ротора, напряжений статора. По данным осциллограмм была синтезирована четырехконтурная схема замещения генератора и на ее основе рассчитана частотная характеристика генератора, приведенная на рис.1.

Рисунок 1 – Частотная характеристика генератора Т-4376/142 по оси d

Далее с помощью данного метода были рассчитаны фазные токи генератора при двухфазном КЗ, для простоты учитывалась лишь первая гармоника. На рис.2 представлены графики расчетных фазных токов и кружками показаны амплитудные величины токов по осциллограмме. Как видно из рисунка, результаты эксперимента и расчета достаточно хорошо совпадают, расхождение не превышает 10%, что для практических расчетов переходных процессов является приемлемым.

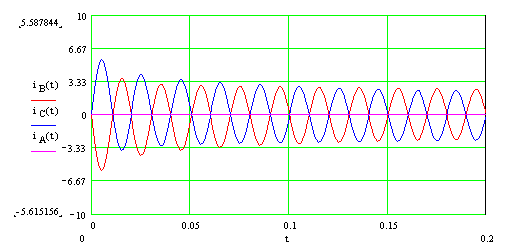
Рисунок 2 – Расчетные фазные токи генератора при двухфазном КЗ и данные осциллограмм

При разработке данного метода было выявлено одно весьма существенное обстоятельство, которое необходимо учитывать в расчетах. Как известно из курса “Переходные процессы”, при несимметричных КЗ величины напряжений различных последовательностей равны между собой; так, например, при двухфазном КЗ фаз B и C напряжения прямой и обратной последовательностей равны и в особой фазе (А) совпадают по направлению. Однако при использовании частотного метода, как выяснилось, для установившегося режима первое условие не может выполняться. Действительно, согласно методу симметричных составляющих ток в фазе A при двухфазном КЗ фаз B и C должен быть равен нулю, что возможно лишь в том случае, если установившиеся токи прямой и обратной последовательностей будут равны друг другу и противоположно направлены. Но величина тока прямой последовательности при единичном напряжении будет численно равна 1/(X_d+X₂), а тока обратной последовательности - 1/X₂. А поскольку величины сопротивлений X_d и X₂ отличаются друг от друга в несколько раз, то при одинаковых напряжениях U₁ и U₂ во столько же раз будут отличаться и указанные токи. Следовательно, для получения правильной физической картины величины U₁ и U₂ должны быть различны. Их можно найти из соотношений:

В случае однофазного и двухфазного на землю КЗ также следует обращать особое внимание на соотношения между симметричными составляющими. Так, при двухфазном КЗ на землю величины напряжений прямой, обратной и нулевой последовательностей не равны между собой, как в метода симметричных составляющих. Критерием правильности выбора величины симметричных составляющих может служить сохранение физической картины в генераторе: при двухфазном КЗ на землю в любой момент времени ток в особой фазе должен равняться нулю, а при однофазном - токи в незамкнувшихся фазах должны быть равны нулю.

Учет внешних сопротивлений при частотном методе осуществляется довольно просто. Он основан на том факте, что частотная характеристика по сути дела есть комплекс тока статора в зависимости от скольжения ротора. Если расчет ведется в относительных единицах и напряжение статора равно единице, то ток статора численно равен проводимости Y_d синхронного генератора, измеренной со стороны статора. Внешнее сопротивление, подключаемое к генератору, отражается на частотной характеристике включением последовательно с Y_d величины, обратной этому сопротивлению. Например, если характеристику обозначить зависимостью Y_d(js), то при включении индуктивного сопротивления в обмотку статора результирующая частотная характеристика будет иметь вид:

Если внешним сопротивлением является трансформатор, то необходимо помнить, что при переходе через него прямая и обратная последовательности повернутся на углы, зависящие от группы соединений трансформатора. При обычной группе "звезда / треугольник - 11" для прямой последовательности этот угол составит 30 градусов, для обратной -30 градусов. Естественно, что при этом они изменятся и по величине.

Как уже было отмечено, при несимметричных КЗ в синхронных генераторах возникает полный спектр гармоник. В этой ситуации постает задача о нахождении количества гармоник, которое, с одной стороны, позволило бы сохранить простоту метода расчета, а с другой - обеспечить достаточную точность расчета. Анализ результатов вычислений и сравнение их с экспериментальными данными показали, что для обеспечения приемлемой точности расчета достаточно учитывать лишь первую гармонику токов прямой и обратной последовательностей.

1) Важнов А. И. Переходные процессы в машинах переменного тока. -Л.: Энергия, 1980. - 256с.

2) Казовский Е.Я. Переходные процессы в электрических машинах переменного тока. - Л.: Энергия, 1962.-624с