Лабораторная работа посвящена исследованию переходных процессов в синхронном явнополюсном генераторе, в частности, внезапного короткого замыкания генератора. Математическая модель лабораторной установки содержит модель синхронного генератора, нагрузки (осуществляющей короткое замыкание) и приводного механизма. Модель является универсальной и пригодна для исследования и других переходных процессов.

Синхронная машина описывается системой 6 дифференциальных уравнений:

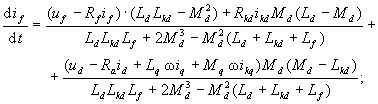
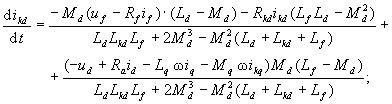
Здесь переменными состояния являются токи:

i_d - ток якоря по оси d;
i_q - ток якоря по оси q;
i_f - ток возбуждения;
i_kd - ток демпферной обмотки по оси d;
i_kq - ток демпферной обмотки по оси q,
и угол Q - электрический угол между осью фазы A и осью d машины.

Для взаимодействия с другими частями электромеханической системы используются мгновенные значения напряжений:

Для простоты компоновки полной модели электромеханической системы из моделей составляющих ее элементов в модели синхронной машины выполняется внутреннее преобразование координат. На входе получаемые извне напряжения фаз u_a, u_b, u_c преобразуются в напряжения по осям d,q:

На выходе токи по осям d,q преобразуются в фазные токи:

Дифференциальные уравнения содержат следующие параметры:

R_a – активное сопротивление обмотки якоря;
L_d – индуктивность самоиндукции обмотки якоря по оси d;
L_kd – индуктивность самоиндукции демпферной обмотки по оси d;
L_f – индуктивность самоиндукции обмотки возбуждения;
L_q – индуктивность самоиндукции обмотки якоря по оси q;
L_kq – индуктивность самоиндукции демпферной обмотки по оси q;
Ls – индуктивность рассеяния обмотки якоря;
R_f – активное сопротивление обмотки возбуждения;
R_kd – активное сопротивление демпферной обмотки по оси d;
R_kq – активное сопротивление демпферной обмотки по оси q;
p – число пар полюсов.

По ним рассчитываются индуктивности взаимоиндукции по осям d,q:

и собственная индуктивность обмотки якоря

где u_н – номинальное напряжение обмотки якоря; S_н – номинальная полная мощность.

Следует отметить, что все уравнения здесь записаны в относительных единицах. Переход к системе относительных единиц осуществляется один раз при первом получении параметров программой по следующим формулам:

Здесь базовые значения сопротивлений определяются как

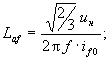
Демпферная обмотка и обмотка возбуждения должны быть приведены к числу витков якоря.

Естественно, что и мгновенные значения величин, которыми модель синхронной машины обменивается с другими моделями, должны претерпевать внутренние преобразования сначала к относительным единицам, а затем обратно к абсолютным. При этом в качестве базовых значений выбираются следующие:

- напряжение якоря;
- полная мощность;
- ток якоря;
- электрическая частота вращения;
- электромагнитный момент;
- напряжение возбуждения;
- ток возбуждения.

В качестве дополнительных величин, которые могут заинтересовать исследователя, рассчитываются и мгновенные значени потокосцеплений (в о.е.):

которые можно перевести в систему фазных координат аналогично токам

Перевод потокосцеплений из относительных единиц в абсолютные осуществляется следующим образом:

Все вышеизложенное относилось к модели электрической машины, самой сложной части электромеханической системы. Другие модели проще. Так, для моделирования короткого замыкания достаточно задать
u_a= 0; u_b = 0; u_c = 0.
Но лучше записать
u_a = i_aR_n; u_b = i_bR_n; u_c = i_cR_n
и изменять R_n – величину сопротивления нагрузки для снятия статических характеристик из расчета динамики и моделирования короткого замыкания путем задания R_n=0.

Модель приводного механизма должна включать в себя и механическую часть синхронного генератора, так как они вращаются как единое жесткое тело. Уравнение движения традиционно записывается в виде:

где W - геометрическая частота вращения (связанная с электрической частотой вращения w соотношением w = W Ч p), рад/с; J –момент инерции, кгЧ м²; T_m – момент приводного механизма, НЧ м; T_эм – электромагнитный момент синхронного генератора, НЧ м. В случае большой мощности приводного механизма можно задаться завышенным значением момента инерции или вообще исключить последнее уравнение, заменив его на w =Const.

На рис. 4.2 приведена кривая изменения тока якоря синхронного генератора при внезапном коротком замыкании, полученная в результате расчета описанной выше математической модели электромеханической системы – лабораторной установки.