Савчук Владимир Павлович, vps@a-teleport.com
7. Основные критерии эффективности инвестиционного проекта и методы их оценки
7. 1. Общая характеристика методов оценки эффективности
Международная практика оценки эффективности инвестиций существенно базируется на концепции временной стоимости денег и основана на следующих принципах:
Суть всех методов оценки базируется на следующей простой схеме:
Исходные инвестиции при реализации какого-либо проекта генерируют
денежный поток CF1, CF2, ... ,
CFn. Инвестиции признаются эффективными, если
этот поток достаточен для
Наиболее распространены следующие показатели эффективности капитальных вложений:
Данные показатели равно как и соответствующие им методы, используются в двух вариантах:
7. 2. Метод дисконтированного периода окупаемости
Рассмотрим этот метод на конкретном примере анализа двух взаимоисключающих друг друга проектов.
Пример 1. Пусть оба проекта предполагают одинаковый объем инвестиций $1,000 и рассчитаны на четыре года.
Проект А генерирует следующие денежные потоки : по годам 500, 400, 300, 100, а проект В - 100, 300, 400, 600. Стоимость капитала проекта оценена на уровне 10%. Расчет дисконтированного срока осуществляется с помощью следующих таблиц.
Таблица 7.1.
Проект А
|
Год |
0 |
1 |
2 |
3 |
4 |
|
Чистый денежный поток (ЧДП) |
-1,000 |
500 |
400 |
300 |
100 |
|
Дисконтированный ЧДП |
-1,000 |
455 |
331 |
225 |
68 |
|
Накопленный дисконтированный ЧДП |
-1,000 |
-545 |
-214 |
11 |
79 |
Во третьей строке таблицы помещены дисконтированные значения денежных доходов предприятия в следствии реализации инвестиционного проекта. В данном случае уместно рассмотреть следующую интерпретацию дисконтирования: приведение денежной суммы к настоящему моменту времени соответствует выделению из этой суммы той ее части, которая соответствует доходу инвестора, который предоставляется ему за то, что он предоставил свой капитал. Таким образом, оставшаяся часть денежного потока призвана покрыть исходный объем инвестиции. В четвертой строке таблицы содержатся значения непокрытой части исходной инвестиции. С течением времени величина непокрытой части уменьшается. Так, к концу второго года непокрытыми остаются только $214, и поскольку дисконтированной значение денежного потока в третьем году составляет $225, становится ясным, что период покрытия инвестиции составляет два полных года и какую-то часть года. Более конкретно для проекта получим:
![]() . Аналогично для второго проекта расчетная таблица и
расчет дисконтированного периода окупаемости имеют следующий вид.
. Аналогично для второго проекта расчетная таблица и
расчет дисконтированного периода окупаемости имеют следующий вид.
Таблица 7.2.
Проект В.
|
Год |
0 |
1 |
2 |
3 |
4 |
|
Чистый денежный поток (ЧДП) |
-1,000 |
100 |
300 |
400 |
600 |
|
Дисконтированный ЧДП |
-1,000 |
91 |
248 |
301 |
410 |
|
Накопленный дисконтированный ЧДП |
-1,000 |
-909 |
-661 |
-360 |
50 |
![]() .
.
На основе результатов расчетов делается вывод о том, что проект А лучше, поскольку он имеет меньший дисконтированный период окупаемости.
Существенным недостатком метода дисконтированного периода окупаемости является то, что он учитывает только начальные денежные потоки, именно те потоки, которые укладываются в период окупаемости. Все последующие денежные потоки не принимаются во внимание в расчетной схеме. Так, если бы в рамках второго проекта в последний год поток составил, например $1000, то результат расчета дисконтированного периода окупаемости не изменился бы, хотя совершенно очевидно, что проект станет в этом случае гораздо более привлекательным.
7. 3. Метод чистого современного значения (NPV - метод)
Этот метод основан на использовании понятия чистого современного значения (Net Present Value)
![]() ,
,
где CFi - чистый денежный поток,
r -
стоимость капитала, привлеченного для инвестиционного проекта.
Термин “чистое” имеет следующий смысл: каждая сумма денег определяется как алгебраическая сумма входных (положительных) и выходных (отрицательных) потоков. Например, если во второй год реализации инвестиционного проекта объем капитальных вложений составляет $15,000, а денежный доход в тот же год - $12,000, то чистая сумма денежных средств во второй год составляет ($3,000).
В соответствии с сущностью метода современное значение всех входных денежных потоков сравнивается с современным значением выходных потоков, обусловленных капитальными вложениями для реализации проекта. Разница между первым и вторым есть чистое современное значение, величина которого определяет правило принятия решения.
Процедура метода.
Шаг 1. Определяется современное значение каждого денежного потока, входного и выходного.
Шаг 2. Суммируются все дисконтированные значения элементов денежных потоков и определяется критерий NPV.
Шаг 3. Производится принятие решения:
Пример 2. Руководство предприятия собирается внедрить новую машину, которая выполняет операции, производимые в настоящее время вручную. Машина стоит вместе с установкой $5,000 со сроком эксплуатации 5 лет и нулевой ликвидационной стоимостью. По оценкам финансового отдела предприятия внедрение машины за счет экономии ручного труда позволит обеспечить дополнительный входной поток денег $1,800. На четвертом году эксплуатации машина потребует ремонт стоимостью $300.
Экономически целесообразно ли внедрять новую машину, если стоимость капитала предприятия составляет 20%.
Решение. Представим условия задачи в виде лаконичных исходных данных.
|
Стоимость машины |
$5,000 |
|
Время проекта |
5 лет |
|
Остаточная стоимость |
$0 |
|
Стоимость ремонта в 4-м году |
$300 |
|
Входной денежный поток за счет приобретения машины |
$1,800 |
|
Показатель дисконта |
20% |
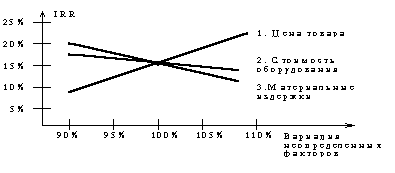
Расчет произведем с помощью следующей таблицы.
Таблица 7.3.
Расчет значения NPV
|
Наименование денежного потока |
Год(ы) |
Денежный поток |
Дисконтирование множителя 20%* |
Настоящее значение денег |
|
Исходная инвестиция |
Сейчас |
($5,000) |
1 |
($5,000) |
|
Входной денежный поток |
(1-5) |
$1,800 |
2.991 |
$5,384 |
|
Ремонт машины |
4 |
($300) |
0.482 |
($145) |
|
Современное чистое значение (NPV) |
$239 | |||
* Множитель дисконтирования определяется с помощью финансовых таблиц.
В результате расчетов NPV = $239 > 0, и поэтому с финансовой точки зрения проект следует принять.
Сейчас уместно остановиться на интерпретации значения NPV. Очевидно, что сумма $239 представляет собой некоторый “запас прочности”, призванный компенсировать возможную ошибку при прогнозировании денежных потоков. Американские финансовые менеджеры говорят - это деньги, отложенные на “черный день”.
Рассмотрим теперь вопрос зависимости показателя и, следовательно, сделанного на его основе вывода от нормы доходности инвестиций. Другими словами, в рамках данного примера ответим на вопрос, что если показатель доходности инвестиций (стоимость капитала предприятия) станет больше. Как должно измениться значение NPV?
Расчет показывает, что при r = 24% получим NPV = ($186), то есть критерий является отрицательным и проект следует отклонить. Интерпретация этого феномена может быть проведена следующим образом. О чем говорит отрицательное значение NPV? О том, что исходная инвестиция не окупается, т.е. положительные денежные потоки, которые генерируются этой инвестицией не достаточны для компенсации, с учетом стоимости денег во времени, исходной суммы капитальных вложений. Вспомним, что стоимость собственного капитала компании - это доходность альтернативных вложений своего капитала, которое может сделать компания. При r = 20% компании более выгодно вложить деньги в собственное оборудование, которое за счет экономии генерирует денежный поток $1,800 в течение ближайших пяти лет; причем каждая из этих сумм в свою очередь инвестируется по 20% годовых. При r = 24% компании более выгодно сразу же инвестировать имеющиеся у нее $5,000 под 24% годовых, нежели инвестировать в оборудование, которое за счет экономии будет “приносить” денежный доход $1,800, который в свою очередь будет инвестироваться под 24% годовых.
Общий вывод таков: при увеличении нормы доходности инвестиций (стоимости капитала инвестиционного проекта) значение критерия NPV уменьшается.
Для полноты представления информации, необходимой для расчета NPV, приведем типичные денежные потоки.
Типичные входные денежные потоки:
Типичные выходные потоки:
Ранее было отмечено, что результирующие чистые денежные потоки, призваны обеспечить возврат инвестированной суммы денег и доход для инвесторов. Рассмотрим, как происходит разделение каждой денежной суммы на эти две части с помощью следующего иллюстрирующего примера.
Пример 3. Предприятие планирует вложить деньги в приобретение нового приспособления которое стоит $3,170 и имеет срок службы 4 года с нулевой остаточной стоимостью. Внедрение приспособления по оценкам позволяет обеспечить входной денежный поток $1,000 в течение каждого года. Руководство предприятия позволяет производить инвестиции только в том случае, когда это приводит к отдаче хотя бы 10% в год.
Решение. Сначала произведем обычный расчет чистого современного значения.
Таблица 7.4.
Традиционный расчет NPV
|
Год(ы) |
Сумма денег |
Множитель дисконтирования |
Настоящее значение | |
|
Исходная инвестиция |
Сейчас |
($3,170) |
1 |
($3,170) |
|
Годовой приток денег |
(1-4) |
$1,000 |
3.170 |
$3,170 |
Таким образом, NPV=0 и проект принимается.
Дальнейший анализ состоит в распределении $1,000 входного потока на две части:
Таблица 7.5.
Расчет распределения денежных потоков
|
Год |
Инвестиция по отношению к данному году |
Поток денег |
Отдача от инвестиции (1) |
Возврат инвестиции (2) - (3) |
Непокрытая инвестиция на конец года (1) - (4) |
|
1 |
2 |
3 |
4 |
5 | |
|
1 |
$3,170 |
$1,000 |
$317 |
$683 |
$2,487 |
|
2 |
$2,487 |
$1,000 |
$249 |
$751 |
$1,736 |
|
3 |
$1,736 |
$1,000 |
$173 |
$827 |
$909 |
|
4 |
$909 |
$1,000 |
$91 |
$909 |
0 |
|
$3,170 |
7. 4. Влияние инфляции на оценку эффективности инвестиций
Анализ влияния инфляции может быть произведен для двух вариантов
В рамках первого подхода, который в большей степени отвечает реальной ситуации, особенно в странах с нестабильной экономикой, метод чистого современного значения используется в своей стандартной форме, но все составляющие расходов и доходов, а также показатели дисконта корректируются в соответствии с ожидаемым темпом инфляции по годам. Важно отметить, что произвести состоятельный прогноз различных темпов инфляции для различных типов ресурсов представляется чрезвычайно трудной и практически неосуществимой задачей.
В рамках второго подхода влияние инфляции носит своеобразный характер: инфляция влияет на числа (промежуточные значения), получаемые в расчетах, но не влияет на конечный результат и вывод относительно судьбы проекта. Рассмотрим это явление на конкретном примере.
Пример 4. Компания планирует приобрести новое оборудование по цене $36,000, которое обеспечивает $20,000 экономии затрат (в виде входного денежного потока) в год в течение трех ближайших лет. За этот период оборудование подвергнется полному износу. Стоимость капитала предприятия составляет 16%, а ожидаемый темп инфляции - 10% в год.
Сначала оценим проект без учета инфляции. Решение представлено в табл. 7.6.
Таблица 7.6.
Решение без учета инфляции
|
Год |
Сумма денег |
16%-ный множитель |
Современное значение | |
|
Исходная инвестиция |
Сейчас |
($36,000) |
1 |
($36,000) |
|
Годовая экономия |
(1-3) |
20,000 |
2.246 |
44,920 |
|
Чистое современное значение |
$8,920 | |||
Из расчетов очевиден вывод: проект следует принять, отмечая высокий запас прочности.
Теперь учтем в расчетной схеме эффект инфляции. Прежде всего необходимо учесть влияние инфляции на требуемое значение показателя отдачи. Для этого вспомним следующие простые рассуждения. Пусть предприятие планирует реальную прибыльность своих вложений в соответствии с процентной ставкой 16 %. Это означает, что при инвестировании $36,000 через год оно должно получить $36,000 х (1+0.16) = $41,760. Если темп инфляции составляет 10 %, то необходимо скорректировать эту сумму в соответствии с темпом: $41,760 х (1+0.10) = $45,936. Общий расчет может быть записан следующим образом
$36,000 х (1+0.16) х (1+0.10) = $45,936.
В общем случае, если rр - реальная процентная ставка прибыльности, а Т - темп инфляции, то номинальная (контрактная) норма прибыльности запишется с помощью формулы
![]()
Для рассматриваемого примера расчет приведенного показателя стоимости капитала имеет вид:
|
реальная стоимость капитала |
16%; |
|
темп инфляции |
10%; |
|
смешанный эффект (10% от 16%) |
1.6%; |
|
приведенная стоимость капитала |
27.6%. |
Рассчитаем величину критерия NPV с учетом инфляции, т.е. пересчитаем все денежные потоки и продисконтируем их с показателем дисконта 27.6%.
Таблица 7.7.
Решение с учетом инфляции
|
Год |
Сумма денег |
Индекс цен |
Привед. денежн. поток |
27.6%-ный множит. |
Наст. значен. | |
|
Исходная инвестиция |
Сейчас |
($36,000) |
- |
($36,000) |
1,000 |
($36,000) |
|
Годовая экономия |
1 |
20,000 |
1.10 |
22,000 |
0.7837 |
17,241 |
|
Годовая экономия |
2 |
20,000 |
1.21 |
24,200 |
0.6142 |
14,864 |
|
Годовая экономия |
3 |
20,000 |
1.331 |
26,620 |
0.4814 |
12,815 |
|
Чистое современное значение |
$8,920 | |||||
Ответы обоих решений в точности совпадают. Результаты получились одинаковыми, так как мы скорректировали на инфляцию как входной поток денег, так и показатель отдачи.
По этой причине большая часть фирм западных стран не учитывает инфляцию при расчете эффективности капитальных вложений.
7. 5. Внутренняя норма прибыльности (IRR)
По определению, внутренняя норма прибыльности (иногда говорят доходности) (IRR) - это такое значение показателя дисконта, при котором современное значение инвестиции равно современному значению потоков денежных средств за счет инвестиций, или значение показателя дисконта, при котором обеспечивается нулевое значение чистого настоящего значения инвестиционных вложений.
Экономический смысл внутренней нормы прибыльности состоит в том, что это такая норма доходности инвестиций, при которой предприятию одинаково эффективно инвестировать свой капитал под IRR процентов в какие-либо финансовые инструменты или произвести реальные инвестиции, которые генерируют денежный поток, каждый элемент которого в свою очередь инвестируется по IRR процентов.
Математическое определение внутренней нормы прибыльности предполагает решение следующего уравнения
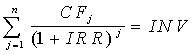 ,
,
где: CFj - входной денежный поток в j-ый
период,
INV - значение инвестиции.
Решая это уравнение, находим значение IRR. Схема принятия решения на основе метода внутренней нормы прибыльности имеет вид:
Таким образом, IRR является как бы “барьерным показателем”: если стоимость капитала выше значения IRR, то “мощности” проекта недостаточно, чтобы обеспечить необходимый возврат и отдачу денег, и следовательно проект следует отклонить.
В общем случае уравнение для определения IRR не может быть решено в конечном виде, хотя существуют ряд частных случаев, когда это возможно. Рассмотрим пример, объясняющий сущность решения.
Пример 5. На покупку машины требуется $16,950. Машина в течение 10 лет будет экономить ежегодно $3,000. Остаточная стоимость машины равна нулю. Надо найти IRR.
Найдем отношение требуемого значения инвестиции к ежегодному притоку денег, которое будет совпадать с множителем какого-либо (пока неизвестного) коэффициента дисконтирования
![]() .
.
Полученное значение фигурирует в формуле определения современного значения аннуитета
![]() .
.
И, следовательно, с помощью финансовой табл. 4 прил. находим, что для n=10 показатель дисконта составляет 12%. Произведем проверку:
|
Годы |
Денежный поток |
12% коэффиц. пересчета |
Настоящее значение | |
|
Годовая экономика |
(1-10) |
$3,000 |
5.650 |
$16,950 |
|
Исходное инвестирование |
Сейчас |
(16.950) |
1.000 |
16,950 |
Таким образом, мы нашли и подтвердили, что IRR=12%. Успех решения был обеспечен совпадением отношения исходной суммы инвестиций к величине денежного потока с конкретным значением множителя дисконта из финансовой таблицы. В общем случае надо пользоваться интерполяцию.
Пример 6. Необходимо оценить значение внутренней нормы доходности инвестиции объемом $6,000, который генерирует денежный поток $1,500 в течение 10 лет.
Следуя прежней схеме рассчитаем коэффициент дисконта:
![]() .
.
По табл. 4 прил. для n=10 лет находим
![]()
Значит значение IRR расположено между 20% и 24%.
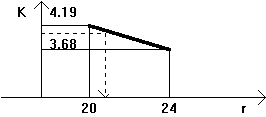
Используя линейную интерполяцию находим
![]() .
.
Существуют более точные методы определения IRR, которые предполагают использование специального финансового калькулятора или электронного процессора EXCEL.
7. 6. Сравнение NPV и IRR методов
К сожалению NPV и IRR методы могут конфликтовать друг с другом. Рассмотрим этот феномен на конкретном примере. Произведем оценку сравнительной эффективности двух проектов с одинаковыми исходными инвестициями, но с различными входными денежными потоками. Исходные данные для расчета эффективности помещены в следующей таблице.
Таблица 7.8
Денежные потоки альтернативных проектов
|
Год |
Проект А |
Проект В |
|
0 |
($1,000) |
($1,000) |
|
1 |
500 |
100 |
|
2 |
400 |
300 |
|
3 |
300 |
400 |
|
4 |
100 |
600 |
Для дальнейшего анализа используем так называемый NPV - профиль, который по определению представляет собой зависимость показателя NPV от стоимости капитала проекта.
Рассчитаем NPV для различных значений стоимости капитала.
Таблица 7.9
Показатели NPV для альтернативных проектов
|
r |
Проект А |
Проект В |
|
0 |
300 |
400 |
|
5 |
180.42 |
206.50 |
|
10 |
78.82 |
49.18 |
|
15 |
(8.33) |
(80.14) |
Графики NPV профилей для проектов будут иметь вид, представленный на рис. 7.1.
Решив уравнения, определяющие внутреннюю норму доходности, получим:
Таким образом, по критерию внутренней нормы доходности предпочтение следует отдать проекту А, как имеющему большее значение IRR. В то же время NPV-метод неоднозначно дает вывод в пользу проекта А.
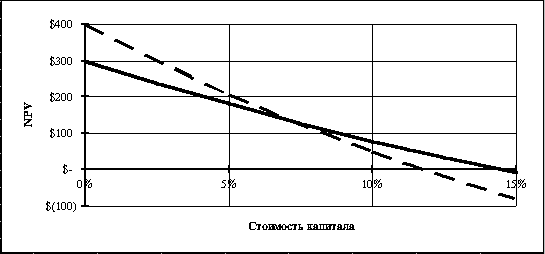
Рис. 7.1. NPV профили альтернативных проектов
Проанализировав соотношение NPV-профилей, которые имеют
пересечение в точке ![]() , составляющей в
данном случае значение 7.2%, приходим к следующему выводу:
, составляющей в
данном случае значение 7.2%, приходим к следующему выводу:
Следует отметить, что этот конфликт имеет место только при анализе взаимоисключающих друг друга проектов. Для отдельно взятых проектов оба метода дают один и тот же результат, положительное значение NPV всегда соответствует ситуации, когда внутренняя норма доходности превышает стоимость капитала.
7. 7. Принятие решения по критерию наименьшей стоимости
Существуют инвестиционные проекты, в которых трудно или невозможно вычислить денежный доход. Подобного рода проекты возникают на предприятии, когда оно собирается модифицировать технологическое или транспортное оборудование, которое принимает участие во многих разноплановых технологических циклах и невозможно оценить результирующий денежный поток. В этом случае в качестве критерия для принятия решения о целесообразности инвестиций выступает стоимость эксплуатации.
Пример 7. Трактор участвует во многих производственных процессах. Нужно решить эксплуатировать старый или купить новый. Исходные данные для принятия решения имеют следующий вид.
|
Исходные данные: |
Старый |
Новый |
|
Стоимость покупки |
- |
$25,000 |
|
Остаточная стоимость сейчас |
$3,000 |
- |
|
Годовые денежные затраты на эксплуатацию |
15,000 |
9,000 |
|
Капитальный ремонт сейчас |
4,000 |
- |
|
Остаточная стоимость через 6 лет |
0 |
5,000 |
|
Время проекта |
6 лет |
6 лет |
Рассчитаем все издержки, которые понесет предприятие, приняв каждую из альтернатив. Для принятия окончательного решения приведем эти издержки к настоящему моменту времени (продисконтируем издержки) и выберем ту альтернативу, которая соответствует меньшему значению дисконтированных издержек.
Таблица 7.10
Расчет дисконтированных издержек при покупке
новой машины
|
Годы |
Денежный |
Коэфф. |
Настоящее значение | |
|
Исходные инвестиции |
Сейчас |
$(25,000) |
1.000 |
$(25,000) |
|
Остаточная стоимость |
Сейчас |
3,000 |
1.000 |
3.000 |
|
Годовая стоимость |
1-6 |
(9,000) |
4.355 |
39,195 |
|
Остаточная стоимость |
6 |
5,000 |
0.564 |
2,820 |
|
Настоящее значение денежных потерь |
$(58,375) | |||
Таблица 7.11
Расчет дисконтированных издержек при
эксплуатации старой машины
|
Годы |
Денежный |
Коэфф. |
Настоящее значение | |
|
Капитальный ремонт |
Сейчас |
$(4,000 |
1.000 |
$(4,000) |
|
Годовая стоимость |
1-6 |
(15,000) |
4.355 |
(65,325) |
|
Настоящее значение денежных потерь |
$(69,325) | |||
Современное значение дисконтированных издержек говорит в пользу покупки новой машины. В этом случае потери будут на $10,950 меньше.
7. 8. Допущения, принятые при оценке эффективности
В заключение отметим одно важное для понимания инвестиционных технологий обстоятельство: какие допущения принимаются при расчете показателей эффективности и в какой мере они соответствуют реальной практике.
При использовании всех методов существенно были использованы следующие два допущения.
Используемые допущения, разумеется, не полностью соответствуют реальному положению дел, однако, учитывая большую продолжительность проектов в целом, не приводят к серьезным ошибкам в оценке эффективности.
Контрольные вопросы и задания
Задания
1. Предприятие требует как минимум 14 процентов отдачи при инвестировании собственных средств. В настоящее время предприятие располагает возможностью купить новое оборудование стоимостью $84,900. Использование этого оборудования позволит увеличить объем выпускаемой продукции, что в конечном итоге приведет к $15,000 дополнительного годового денежного дохода в течение 15 лет использования оборудования. Вычислите чистое современное значение проекта, предположив нулевую остаточную стоимость оборудования через 15 лет.
Решение.
Расчет проведем используя таблицу, находя множитель дисконтирования с помощью финансовых таблиц.
|
Наименование денежного потока |
Год(ы) |
Денежный поток |
Множитель дисконтирования |
Настоящее значение денег |
|
Исходная инвестиция |
Сейчас |
($84,900) |
1 |
($84,900) |
|
Входной денежный поток |
(1-15) |
$15,000 |
6.1422 |
$92,133 |
|
Чистое современное значение |
$7,233 | |||
Чистое современное значение оказалось положительным, что свидетельствует в пользу принятия проекта.
2. Предприятие планирует новые капитальные вложения в течение двух лет: $120,000 в первом году и $70,000 - во втором. Инвестиционный проект рассчитан на 8 лет с полным освоением вновь введенных мощностей лишь на пятом году, когда планируемый годовой чистый денежный доход составит $62,000. Нарастание чистого годового денежного дохода в первые четыре года по плану составит 30%, 50%, 70%, 90% соответственно по годам от первого до четвертого. Предприятие требует как минимум 16 процентов отдачи при инвестировании денежных средств.
Необходимо определить
Решение.
1. Определим чистые годовые денежные доходы в процессе реализации инвестиционного проекта:
в первый год - $62,000 ![]() 0.3 = $18,600;
0.3 = $18,600;
во второй год - $62,000 ![]() 0.5 = $31,000;
0.5 = $31,000;
в третий год - $62,000 ![]() 0.7 = $43,400;
0.7 = $43,400;
в четвертый год - $62,000 ![]() 0.9 = $55,800;
0.9 = $55,800;
во все оставшиеся годы - $62,000.
2. Расчет чистого современного значения инвестиционного проекта произведем с помощью таблицы.
|
Наименование денежного потока |
Год(ы) |
Денежный |
Множитель дисконтирования |
Настоящее |
|
Инвестиция |
Сейчас |
($120,000) |
1 |
$ (120,000) |
|
Инвестиция |
1 |
($70,000) |
0.8621 |
$ (60,347) |
|
Денежный доход |
1 |
$18,600 |
0.8621 |
$ 16,035 |
|
Денежный доход |
2 |
$31,000 |
0.7432 |
$ 23,039 |
|
Денежный доход |
3 |
$43,400 |
0.6407 |
$ 27,806 |
|
Денежный доход |
4 |
$55,800 |
0.5523 |
$ 30,818 |
|
Денежный доход |
5 |
$62,000 |
0.4761 |
$ 29,518 |
|
Денежный доход |
6 |
$62,000 |
0.4104 |
$ 25,445 |
|
Денежный доход |
7 |
$62,000 |
0.3538 |
$ 21,936 |
|
Денежный доход |
8 |
$62,000 |
0.3050 |
$ 18,910 |
|
Чистое современное значение инвестиционного проекта |
$ 13,161 | |||
3. Для определения дисконтированного периода окупаемости рассчитаем величины чистых денежных потоков по годам проекта. Для этого необходимо всего лишь найти алгебраическую сумму двух денежных потоков в первый год проекта. Она составит ($60,347) + $16,035 = ($44,312). Остальные значения в последней колонке предыдущей таблицы представляют собой чистые значения.
4. Расчет дисконтированного периода окупаемости произведем с помощью таблицы, в которой будем рассчитывать накопленный дисконтированный денежный поток по годам проекта.
|
Год |
Дисконтированный денежный поток |
Накопленный денежный поток |
|
0 |
($120,000) |
($120,000) |
|
1 |
($44,312) |
($164,312) |
|
2 |
$23,039 |
($141,273) |
|
3 |
$27,806 |
($113,466) |
|
4 |
$30,818 |
($82,648) |
|
5 |
$29,518 |
($53,130) |
|
6 |
$25,445 |
($27,685) |
|
7 |
$21,936 |
($5,749) |
|
8 |
$18,910 |
$13,161 |
Из таблицы видно, что число полных лет окупаемости проекта составляет 7. Дисконтированный срок окупаемости поэтому составит
![]() года.
года.
3. Предприятие имеет два варианта инвестирования имеющихся у него $100,000. В первом варианте предприятие вкладывает в основные средства, приобретая новое оборудование, которое через 6 лет (срок инвестиционного проекта) может быть продано за $8,000; чистый годовой денежный доход от такой инвестиции оценивается в $21,000.
Согласно второму варианту предприятие может инвестировать деньги в рабочий капитал (товарно-материальные запасы, увеличение дебиторских) и это позволит получать $16,000 годового чистого денежного дохода в течение тех же шести лет. Необходимо учесть, что по окончании этого периода рабочий капитал высвобождается (продаются товарно-материальные запасы, закрываются дебиторские счета).
Какой вариант следует предпочесть, если предприятие рассчитывает на 12% отдачи на инвестируемые им денежные средства? Воспользоваться методом чистого современного значения.
Решение.
1. Представим исходные данные задачи в компактном виде.
|
Проект |
1 |
2 |
|
Инвестиции в основные средства..................... |
$100,000 |
- |
|
Инвестиции в рабочий капитал........................ |
- |
$100,000 |
|
Годовой денежный доход.................................. |
$21,000 |
$16,000 |
|
Остаточная стоимость оборудования ............... |
$8,000 |
- |
|
Высвобождение рабочего капитала.................. |
- |
$100,000 |
|
Время проекта.................................................... |
6 лет |
6 лет |
Заметим еще раз, что рабочий капитал и оборудование планируются быть реализованными только по истечении 6 лет.
2. Произведем расчеты чистого современного значения для первого проекта.
|
Наименование |
Год(ы) |
Денежный |
Множитель дисконтирования |
Настоящее |
|
Инвестиция |
Сейчас |
($100,000) |
1.000 |
($100,000) |
|
Денежный доход |
1-6 |
$21,000 |
4.112 |
$86,352 |
|
Продажа оборудов. |
6 |
$8,000 |
0.507 |
$4.056 |
|
Чистое современное значение |
($9,592) | |||
3. Аналогичные расчеты проведем для второго проекта
|
Наименование |
Год(ы) |
Денежный |
Множитель дисконтирования |
Настоящее |
|
Инвестиция |
Сейчас |
($100,000) |
1.000 |
($100,000) |
|
Денежный доход |
1-6 |
$16,000 |
4.112 |
$65,792 |
|
Высвобождение |
6 |
$100,000 |
0.507 |
$50,700 |
|
Чистое современное значение |
$16,492 | |||
4. По результатам расчетов можно сделать следующие выводы:
4. Предприятие планирует крупный инвестиционный проект, предусматривающий приобретение основных средств и капитальный ремонт оборудования, а также вложения в оборотные средства по следующей схеме:
В конце инвестиционного проекта предприятие рассчитывает реализовать оставшиеся основные средства по их балансовой стоимости $25,000 и высвободить часть оборотных средств стоимостью $35,000.
Результатом инвестиционного проекта должны служить следующие чистые (т.е. после уплаты налогов) денежные доходы:
|
1 год |
2 год |
3 год |
4 год |
5 год |
6 год |
7 год |
8 год |
|
$20,000 |
$40,000 |
$40,000 |
$40,000 |
$50,000 |
$50,000 |
$20,000 |
$10,000 |
Необходимо рассчитать чистое современное значение инвестиционного проекта и сделать вывод о его эффективности при условии 12-ти процентной требуемой прибыльности предприятия на свои инвестиции.
Решение.
Схема решения задачи остается прежней. Составляем таблицу расчетных данных и определяем дисконтированные значения всех денежных потоков.
Проект следует принять, поскольку его чистое современное значение существенно положительное.
|
Наименование денежного потока |
Год |
Денежный |
Множитель дисконта |
Настоящее |
|
Приобретение основных средств |
0 |
($130,000) |
1 |
($130,000) |
|
Инвестирование в оборотные средства |
1 |
($25,000) |
0.893 |
($22,325) |
|
Денежный доход в первый год |
1 |
$20,000 |
0.893 |
$17,860 |
|
Инвестирование в оборотные средства |
2 |
($20,000) |
0.797 |
($15,940) |
|
Денежный доход во второй год |
2 |
$40,000 |
0.797 |
$31,880 |
|
Денежный доход в третий год |
3 |
$40,000 |
0.712 |
$28,480 |
|
Денежный доход в четвертый год |
4 |
$40,000 |
0.636 |
$25,440 |
|
Приобретение основных средств |
4 |
($15,000) |
0.636 |
($9,540) |
|
Денежный доход в пятый год |
5 |
$50,000 |
0.567 |
$28,350 |
|
Ремонт оборудования |
6 |
($10,000) |
0.507 |
($5,070) |
|
Денежный доход в шестой год |
6 |
$50,000 |
0.507 |
$25,350 |
|
Денежный доход в седьмой год |
7 |
$20,000 |
0.452 |
$9,040 |
|
Денежный доход в восьмой год |
8 |
$10,000 |
0.404 |
$4,040 |
|
Продажа оборудования |
8 |
$25,000 |
0.404 |
$10,100 |
|
Высвобождение оборотных средств |
8 |
$35,000 |
0.404 |
$14,140 |
|
Чистое современное значение |
$11,805 | |||
5. Предприятие требует как минимум 18 процентов отдачи при инвестировании собственных средств. В настоящее время предприятие располагает возможностью купить новое оборудование стоимостью $84,500. Использование этого оборудования позволит увеличить объем выпускаемой продукции, что в конечном итоге приведет к $17,000 дополнительного годового денежного дохода в течение 15 лет использования оборудования. Вычислите чистое современное значение проекта, предположив, что после окончания проекта оборудование может быть продано по остаточной стоимости $2,500.
6. Предприятие планирует новые капитальные вложения в течение трех лет: $90,000 в первом году, $70,000 - во втором и $50,000 - третьем. Инвестиционный проект рассчитан на 10 лет с полным освоением вновь введенных мощностей лишь на пятом году, когда планируемый годовой чистый денежный доход составит $75,000. Нарастание чистого годового денежного дохода в первые четыре года по плану составит 40%, 50%, 70%, 90% соответственно по годам от первого до четвертого. Предприятие требует как минимум 18 процентов отдачи при инвестировании денежных средств.
Необходимо определить
Как изменится Ваше представление об эффективности проекта, если требуемый показатель отдачи составит 20%.
7. Предприятие имеет два варианта инвестирования имеющихся у него $200,000. В первом варианте предприятие вкладывает в основные средства, приобретая новое оборудование, которое через 6 лет (срок инвестиционного проекта) может быть продано за $14,000; чистый годовой денежный доход от такой инвестиции оценивается в $53,000.
Согласно второму варианту предприятие может инвестировать деньги частично ($40,000) в приобретение новой оснастки, а оставшуюся сумму в рабочий капитал (товарно-материальные запасы, увеличение дебиторских). Это позволит получать $,34000 годового чистого денежного дохода в течение тех же шести лет. Необходимо учесть, что по окончании этого периода рабочий капитал высвобождается (продаются товарно-материальные запасы, закрываются дебиторские счета).
Какой вариант следует предпочесть, если предприятие рассчитывает на 14% отдачи на инвестируемые им денежные средства? Воспользоваться методом чистого современного значения.
8. Предприятие рассматривает инвестиционный проект, предусматривающий приобретение основных средств и капитальный ремонт оборудования, а также вложения в оборотные средства по следующей схеме:
В конце инвестиционного проекта предприятие рассчитывает реализовать оставшиеся основные средства по их балансовой стоимости $15,000 и высвободить оборотные средства.
Результатом инвестиционного проекта должны служить следующие чистые (т.е. после уплаты налогов) денежные доходы:
|
1 год |
2 год |
3 год |
4 год |
5 год |
6 год |
7 год |
8 год |
|
$15,000 |
$25,000 |
$30,000 |
$40,000 |
$40,000 |
$40,000 |
$30,000 |
$20,000 |
Необходимо рассчитать чистое современное значение инвестиционного проекта и сделать вывод о его эффективности при условии 14-ти процентной требуемой прибыльности предприятия на свои инвестиции.
9. Проект, требующий инвестиций в размере $160000, предполагает получение годового дохода в размере $30000 на протяжении 15 лет. Оцените целесообразность такой инвестиции, если коэффициент дисконтирования - 15%.
10. Проект, рассчитанный на 15 лет, требует инвестиций в размере $150000. В первые 5 лет никаких поступлений не ожидается, однако в последующие 10 лет ежегодный доход составит $50000. Следует ли принять этот проект, если коэффициент дисконтирования равен 15%?
11. Анализируются проекты ($):
|
IC |
C1 |
C2 | |
|
А |
-4000 |
2500 |
3000 |
|
Б |
-2000 |
1200 |
1500 |
Ранжируйте проекты по критериям IRR, NPV, если r = 10%.
12. Для каждого из нижеприведенных проектов рассчитайте NPV и IRR, если значение коэффициента дисконтирования равно 20%.
|
А |
-370 |
- |
- |
- |
- |
1000 |
|
В |
-240 |
60 |
60 |
60 |
60 |
- |
|
С |
-263,5 |
100 |
100 |
100 |
100 |
100 |
13. Проанализируйте два альтернативных проекта, если цена капитала 10%.
|
А |
-100 |
120 |
|||
|
Б |
-100 |
- |
- |
- |
174 |
14. Сравните по критериям NPV, IRR два проекта, если стоимость капитала 13%:
|
А |
-20000 |
7000 |
7000 |
7000 |
7000 |
|
Б |
-25000 |
2500 |
5000 |
10000 |
20000 |
15. Величина требуемых инвестиций по проекту равна $18000; предполагаемые доходы: в первый год - $1500, в последующие 8 лет по $3600 ежегодно. Оцените целесообразность принятия проекта, если стоимость капитала 10%.
16. Предприятие рассматривает целесообразность приобретения новой технологической линии. На рынке имеются две модели со следующими параметрами ($)
|
П1 |
П2 | |
|
Цена |
9500 |
13000 |
|
Генерируемый годовой доход |
2100 |
2250 |
|
Срок эксплуатации |
8 лет |
12 лет |
|
Ликвидационная стоимость |
500 |
800 |
|
Требуемая норма доходности |
11% |
11% |
Какой проект Вы предпочтете?