Захаров П.А.
Нижегородский государственный технический университет
Захаров А.М.
Ивановский государственный энергетический университет

Исследование переходных режимов работы АД

Область применения регулируемых электроприводов переменного тока и в нашей стране, и за рубежом в значительной степени расширяется. Особенно это относится к асинхронным электроприводам со статическими преобразователями энергии и двигателями с короткозамкнутым ротором. Эта тенденция обусловлена в большей мере конструктивной простотой и надежностью такого типа двигателей, а также технологичностью их изготовления, сравнительно низкой стоимостью и удобством в эксплуатации. Однако двигатель, как объект автоматического управления представляет собой сложную динамическую структуру, описываемую системой нелинейных дифференциальных уравнений высокого порядка. По этой причине применение такого описания в разработках систем управления асинхронным электроприводом в большинстве случаев оказывается проблематичным. Практически, чаще всего в задачах управления пользуются упрощенными линеаризованными вариантами динамических моделей, что приводит на практике к ухудшению качества процессов регулирования координат асинхронного электропривода.

Вопросы разработки динамических моделей асинхронного двигателя неоднократно ставился в работах [5, 6]. Однако существующие модели в ряде случаев дают существенные ошибки. В то же время в связи расширением области применения, особенно высокоточных электроприводов требуются уточненные модели.

Таким образом, разработка математического описания электромагнитных и электромеханических процессов в асинхронном электроприводе, учитывающих реальный характер нелинейных процессов в асинхронном электродвигателе при условии максимального снижения порядка дифференциальных уравнений, а также использование такой структуры математического описания при разработке регулируемых асинхронных электроприводов, представляется актуальной.

Вывод уравнений описывающих электромагнитные и электромеханические процессы в асинхронном электроприводе, учитывающих нелинейный характер протекания процессов в двигателе осуществлен в [1, 3]. Полученные исходные уравнения имеют следующий вид:

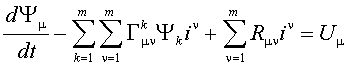	(1)
	(2)
	(3)
	(4)

где Y_m - фазные потокосцепления двигателя; iⁿ - фазные токи; U_m - фазные напряжения; R_mn - параметры двигателя; m - суммарное число фаз статора и ротора двигателя; J - суммарный момент инерции движущихся частей электропривода, приведенных к валу двигателя; J_w - момент количества движения, приведенный к валу двигателя; M_C - момент статического сопротивления; M_Э - электромагнитный момент двигателя; - слагаемое содержащее информацию о дополнительных электродвижущих силах в двигателе и связанных с ними перераспределениях токов и потокосцеплений, не учитываемых при обычном описании; G_mn^k - символ Кристоффеля, в геометрическом смысле отражает кривизну пространства зарядов.

Система уравнений (1)-(4) выведена на основе математического аппарата тензорного анализа [4] и представлена в тензорной форме.

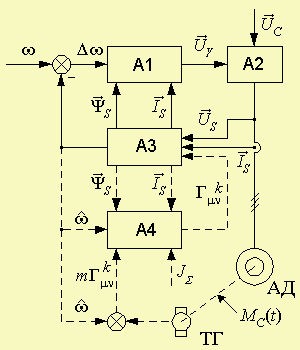Рис. 1. Асинхронный электропривод с датчиками тока и напряжения статора и с идентификатором состояния построенным на основе тензорных уравнений.

В регулируемом асинхронном электроприводе, построеном на базе асинхронного двигателя с короткозамкнутым ротором, управление как потоком, так и моментом осуществляется через статорную цепь. При этом ни одна из электромагнитных переменных, исключая напряжение питания, в общем случае не задана. Используя полученную систему уравнений, можно осуществить наиболее полный анализ процессов в электроприводе переменного тока.

В общем случае структура асинхронного электропривода, построенная по уравнениям (1)-(4), представлена на рис. 1. Настройка системы и определение масштабов динамических параметров осуществляется с использованием скользящих режимов. Повышение качества регулирования в асинхронном электроприводе, построенном по такой структуре обеспечивается тем, что учет динамических параметров дает адекватное описание электромагнитных и электромеханических процессов в асинхронном электродвигателе. Полученная структура асинхронного электропривода отличается от известных наличием дополнительного блока А4, предназначенного для восстановления динамических параметров двигателя. Реализация данного блока осуществляется с использованием скользящих режимов. Блок А1 выполняет функцию векторной ориентации и формирования векторных переменных двигателя, блок А2 - преобразователь, блок А3 - идентификатор, построенный по уравнениям (1)-(4).

Обобщенная методика преобразования тензорных уравнений электромагнитных процессов в асинхронном электроприводе к векторной форме для случая различных переменных входящих в тензорные уравнения осуществляется следующим образом:

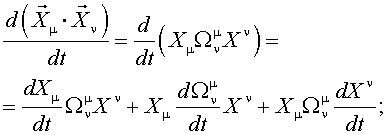	(5)
	(6)
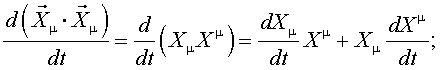	(7)
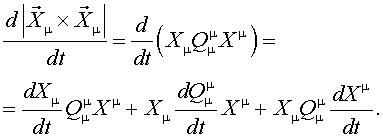	(8)

Различные варианты динамических моделей с ориентацией переменных относительно векторов тока статора, потокосцепления статора, потокосцепления ротора, напряжения статора и т. д. могут быть получено из (1)-(4) с помощью таблицы 1 и действий над тензорами известными из тензорного анализа по методике (5)-(8).

Один из вариантов уравнений электромагнитных процессов в асинхронном двигателе с учетом их нелинейного характера, выведенные с использованием методики приведенной выше, имеют следующий вид:

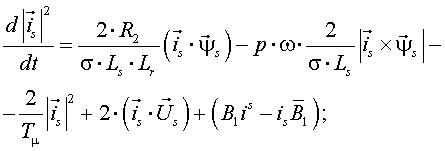	(9)
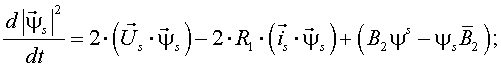	(10)
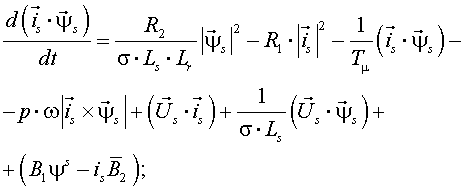	(11)
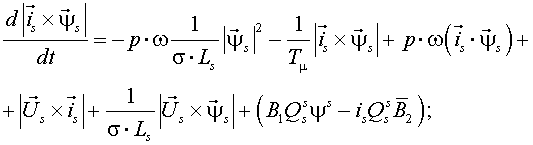	(12)
	(13)
	(14)
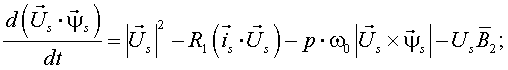	(15)
	(16)
	(17)

где , , , .

Таблица 1

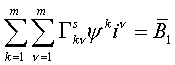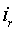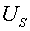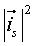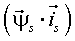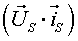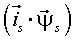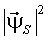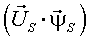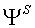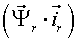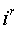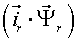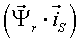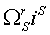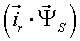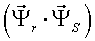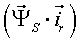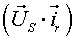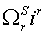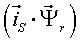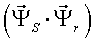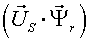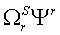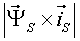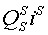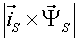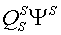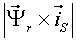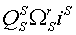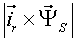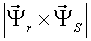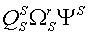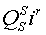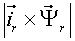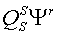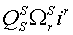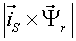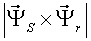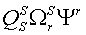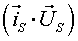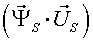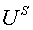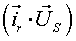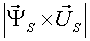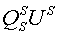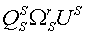По (9)-(17) осуществляется расчет статических и динамических режимов работы асинхронного двигателя с учетом нелинейного характера протекания электромагнитных процессов в нем. Система дифференциальных уравнений (9) - (17), выраженная через переменные в установившемся режиме преобразуется к виду, при котором обнуляются левые части выражений и дополнительные слагаемые учитывающие нелинейный характер процессов.

Углы между векторами напряжения статора, током статора и потокосцепления статора связаны между собой (рис. 2):

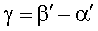(18)

где aў - угол между тока статора и вектором потокосцепления статора; bў - угол между тока статора и вектором напряжения статора; g - угол между вектором потокосцепления статора и вектором напряжения статора.

В режиме холостого хода двигателя (w = w₀), в установившемся режиме, из уравнений (9)-(11) путем несложных преобразований можно получить

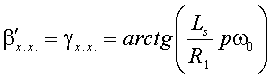(19)

то есть угол между вектором потокосцепления ротора и вектором напряжения при холостом ходе двигателя определяется только параметрами двигателя и выходной частотой преобразователя. В том же режиме модуль вектора потокосцепления статора и модуль вектора потокосцепления ротора связаны с модулем вектора напряжения соотношениями:

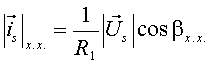	(20)
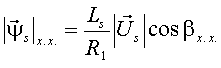	(21)

где индекс "х.х." обозначает величины, относящиеся к режиму холостого хода двигателя.

Рис.2. Пространственное расположение векторных переменных в асинхронном электродвигателе

Полученые уравнения служат для определения начальных условий при расчете переходных режимов.

Методика асимптотического разложения коэффициентов связности в динамической модели электромагнитных процессов в асинхронном электроприводе при переменной частоте вращения вала двигателя приведена ниже. Данные коэффициенты позволяют учесть нелинейный характер процессов, в частности, перераспределение вектора плотности тока по сечению проводников ротора асинхронного двигателя с короткозамкнутым ротором.

Для определения способа введения коэффициентов в модель двигателя переменные G_mn^k расписываются следующим образом

	(22)
	(23)

В состав уравнения входят как векторные, так и тензорные переменные, что некорректно. Необходимо тензорные переменные представить в векторной форме. Для этого используется таблица 1, применяются действия над тензорами, известные из аппарата тензорного анализа. В первом приближении G_mn^k заменяем следующим образом:

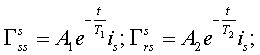	(24)
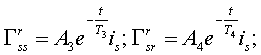	(25)
	(26)
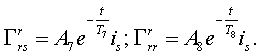	(27)

где A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, - масштабы параметров G_mn^k; T₁, T₂, T₃, T₄, T₅, T₆, T₇, T₈, - постоянные времени.

Полученые коэффициенты позволяют учесть зависимость параметров электрической машины от электромагнитных процессов.

Для проверки устойчивости динамической системы использовался первый метод Ляпунова. Анализ полученных результатов показал, что решение системы уравнений, описывающих электромагнитные процессы в асинхронном электроприводе с инвариантной ориентацией векторных переменных с учетом динамических параметров системы, выходит на установившийся режим.

Рис.3. Экспериментальные осциллограммы прямого пуска вхолостую асинхронного двигателя МТВ 311-6 (11.0 кВт, 380 В, 945 об/мин)

Для подтверждения работоспособности разработанных моделей и адекватности получаемых результатов реальным процессам в двигателе, было произведено сопоставление результатов. Поскольку основным критерием, по которому можно оценить достоверность получаемой информации, является эксперимент, то результаты расчетов сопоставлялись с экспериментальными данными.

Рис.4. Результаты расчета по разработанной методике

Сопоставление результатов показало, что реальные диаграммы скорости и момента получаемые в режиме прямого пуска асинхронного двигателя существенно отличаются от результатов получаемых при расчете по уравнениям Парка-Горева. Для двигателя МТВ 311-6 расхождение расчетного времени пуска по уравнениям (9)-(17) с экспериментом составляет 12%, тогда как время пуска по уравнениям Парка-Горева в два раза превышает эксперимент. Пусковой момент при расчете по предложенной методике отличается от эксперимента на 7%, расхождение при расчете по уравнениям Парка-Горева составляет 15%. Количество пульсаций момента при пуске при расчете по изложенной в работе методике совпадают и составляют 2, тогда как при классической методике момент имеет 4-5 пульсаций.

Рис.5. Результаты расчета по уравнениям Парка-Горева.

Таким образом новая модель асинхронного двигателя, полученная на основе тензорного анализа и позволяющая осуществлять учет нелинейного характера протекания электромагнитных процессов в двигателе при переменной частоте вращения уточняющая расчеты по различным показателям на 6-25% в зависимости от мощности используемого двигателя.

ЛИТЕРАТУРА

1. Архангельский Н. Л., Курнышев Б. С, Захаров П. А. Применение тензорной методологии к описанию электромагнитных процессов в асинхронном двигателе. - М.: Энергоатомиздат, Электричество, 1995, № 2. - С. 37-39.
2. Захаров П. А. Расчет установившихся режимов асинхронного электропривода. - В сб.: Электрооборудование промышленных установок. - Н.Новгород: НГТУ, 1996. - С. 79 - 84.
3. Захаров П. А. Расчет переходных процессов в асинхронном электроприводе с использованием тензорной методологии. - В сб: Оптимизация режимов работы систем электроприводов. - Красноярск: КГТУ, 1997. - С. 33 - 37.
4. Крон Г. Применение тензорного анализа в электротехнике. - М.-Л.: Госэнергоиздат, 1955. - 276 с.
5. Петров Л.П. Управление пуском и торможением асинхронного двигателя. - М.: Энергоатомиздат, 1981. - 184 с.
6. Электромагнитные переходные процессы в асинхронном электроприводе / Соколов М. М., Петров Л. П. Масандилов Л. Б., Ладензон В. А. - М. : Энергия, 1967. - 200 с.
7. Чиликин М. Г., Соколов М. М., Терехов В. М., Шинянский А. В. Основы автоматизированного электропривода. - М.: Энергия, 1974. - 568 с.