УДК 621.86.01

СТАТИСТИЧЕСКАЯ ГИПОТЕЗА ГРАНУЛОМЕТРИЧЕСКОГО СОСТАВА ГРУЗОПОТОКА

Кандидаты техн. наук А.Я.ГРУДАЧЕВ, В.А.КИСЛУН, инж. А.Н.ТКАЧУК (ДонГТУ)

Одним из основных параметров в расчете любой транспортной установки является насыпная плотность перемещаемого материала. Причем, при ее определении следует учитывать, что даже в самом грубом приближении насыпные грузы не могут быть описаны как детерминированные по своим свойствам [1].

В настоящее время известны исследования вероятностного характера свойств насыпных грузов, транспортируемых в горнорудной промышленности [1, 2]. Однако некоторые массовые грузы, которые характерны для предприятий горного машиностроения, с этой точки зрения практически не изучены. Это обстоятельство обусловливает неточности расчета применяемых на данных предприятиях средств транспорта.

В настоящей работе предпринята попытка разработки методики определения вероятностного значения насыпной плотности груза на примере поточной линии штамповочного производства на заводах горного машиностроения.

Основополагающим моментом в вероятностной характеристике насыпной плотности груза является его гранулометрический состав: объем, масса и размер куска - максимальный линейный размер отдельных частиц, а также содержание в общем объеме груза частиц различных фракций.

Вопросы определения линейных размеров отдельных частиц при ограниченном числе их типов не предоставляет сложности. Масса и объем отдельных частиц могут быть определены как прямым измерением, так и по методике, изложенной в [1] с использованием понятия "описанный объем". Однако, содержание в объеме груза частиц различных типов, т.е. их концентрацию, определить затруднительно, особенно при наличии большого числа пунктов поступления груза в единый транспортный поток, например, на сборный конвейер. При больших объемах неоднородного насыпного груза для статистического описания его свойств предлагается к использованию следующая методика.

Пусть на сборный конвейер поступает ряд грузопотоков Q1 , Q2 ,..., Qi, гранулометрический состав которых известен. Другими словами, для каждого из поступающих грузопотоков известно число частиц каждого типа в единичном объеме. Это соответствует реальности, т.к., например, для штамповочного производства гранулометрический состав поступающего в транспортную систему отдельного грузопотока определяется технологией конкретного производственного процесса.

Схема преобразования грузопотока представлена на рисунке.

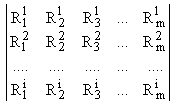
Исходя из принятой гипотезы детерминированности i-тых грузопотоков, можно утверждать, что известным является число частиц каждого типа груза от 1 до m в каждом грузопотоке, т.е. первый грузопоток Q1 содержит частиц каждого из рассматриваемых m типов груза, второй грузопоток Q2 образован числами каждого типа груза и т.д.

В общем случае для всех грузопотоков может быть записана матрица:

. (1)

 

 

Данная матрица может являться характеристикой выходного потока. Так, сумма столбцов матрицы характеризует количество в выходном потоке частиц одного типа, а сумма всех членов матрицы дает общее число частиц в Qвых.

Однако при этом следует учитывать, что в некоторых схемах транспорта отдельные технологические грузопотоки поступают в общее загрузочное устройство, из которого порционно подаются на сборный конвейер. В этом случае гранулометрический состав порции носит вероятностный характер, а его статистические характеристики могут быть определены аналитическим путем.

Составим вероятностное пространство, состоящее из элементарных событий, заключающихся в том, что из K частиц вырабатывают без возвращения порцию из R частиц. Согласно методике [2], число событий, образующих данное пространство:

. (2)

Событие, вероятность которого требуется отыскать, заключается в том, что рассматриваемая порция имеет определенный гранулометрический состав. Другими словами, в порции содержится R1, R2,...Rm частиц каждого типа, причем:

. (3)

Согласно теории комбинаторики [3], число благоприятных исходов равно:

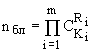. (4)

Тогда вероятность данного гранулометрического состава имеет вид:

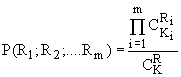, (5)

где - число всех сочетаний из K по R.

Формула (5) представляет собой общий случай гипергеометрического распределения случайной величины

.

То есть, вероятность того, что в данной порции груза содержится R1, R2,... Rm частиц различных типов распределена по гипергеометрическому закону и является многомерной случайной величиной.

Однако, чаще при проектировании транспортных устройств необходимо знать вероятность появления в грузопотоке определенного числа частиц максимальных размеров, то есть частиц одного типа. Пусть, например, частицы первого типа имеют максимальный размер. Тогда необходимо найти вероятность появления в грузопотоке частиц данного типа. В этом случае можно пользоваться формулой (5). При m=2 получаем искомое распределение случайной величины: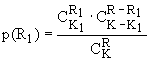

, (6)

где R1 - число частиц первого типа в порции груза;

R - общее число частиц в порции груза;

K - число частиц в общем объеме груза;

K1 - число частиц максимального размера в общем объеме груза.

Формула (6) описывает двумерное гипергеометрическое распределение. Математическое ожидание случайной величины, распределенной по гипергеометрическому закону [3]:

. (7)

Дисперсия случайной величины, распределенной по гипергеометрическому закону [3]:

. (8)

Аналогично можно получить распределения случайных величин R2, R3,.... Rm , т.к. концентрации частиц каждого типа в порции груза являются случайными величинами, распределенными по геометрическому закону. Причем из формулы (5) следует, что изменение любой из них влияет на величины других случайных величин, то есть они являются зависимыми между собой.

Поэтому транспортируемый груз можно считать целостным вероятностным объектом, параметры которого обладают статистической устойчивостью.

Однако структура формулы (5) довольно сложна, даже при m = 2 ею трудно пользоваться при практических расчетах гранулометрических составов грузов.

Поэтому при больших K и K1 можно воспользоваться следующим утверждением: при и с соблюдением условия , можно считать:

. (9)

Для формулы (6) имеем:

. (10)

То есть, при больших K и K1 гипергеометрическое распределение апроксимируется биномиальным, что позволяет применить к определению гранулометрического состава груза предельные теоремы теории вероятностей.

Таким образом, случайная величина Ri , выражающая число частиц определенного типа в порции груза, является величиной, распределенной по гипергеометрическому закону, который при практических расчетах можно заменять биномиальным законом.

Рассмотрим возможность применения предельных теорем к определению гранулометрического состава.

Пусть концентрация частиц определенного типа в объеме груза равна:

, (11)

где Ki - число частиц i-го типа в объеме груза;

K - общее число частиц в объеме груза.

Тогда концентрация остальных частиц в объеме

qi = 1 - pi . (12)

Согласно изложенному выше, случайная величина Ri распределена по биномиальному закону: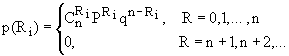

(13)

То есть, при , и значениях Pi » 1/2 справедливо выражение:

. (14)

Математическим ожиданием числа частиц i-го типа является

M[Ri] = n× Pi . (15)

Дисперсией этой случайной величины является

D[Ri] = n× pi× qi . (16)

В этих зависимостях n - число частиц в случайно выбранной порции груза.

Приведенная выше методика определения гранулометрического состава грузопотока является статистической гипотезой, описывающей распределение случайной величины по биномиальному закону.

Авторами были получены практические результаты исследований грузопотоков на предприятиях горно-шахтного машиностроения, подтверждающие справедливость приведенных в работе теоретических выводов.

Библиографический список

1. Дьяков В.А., Гончаревич И.Ф. Транспортные машины и комплексы. - М.: Недра, 1989. - 350с.

2. Шахмейстар Л.Г. Влияние различных децентрирующих факторов на боковой сход ленты. // Известия высших учебных заведений. Горный журнал. - 1982. -№7.

3. Севастьянов Б.А. Курс теории вероятности и математической статистики. - М.: Наука, 1982. - 254с.