. (1)УДК 621.867.13
ИССЛЕДОВАНИЕ ПРОЦЕССА ПЕРЕМЕЩЕНИЯ ФЕРРОМАГНИТНОГО ГРУЗА ДВИЖУЩИМСЯ МАГНИТНЫМ ПОЛЕМ
Исследована кинематика движения ферромагнитной частицы под воздействием движущегося магнитного поля.
The kinematics of motion of a ferromagnetic fragment under effect of a driving magnetic field is investigated.
На частицу отходов штамповочного производства в зоне транспортирования движущимся магнитным полем действуют: магнитная сила
F, сила тяжести mg и сила трения Fтр. Магнитную силу целесообразно разложить на две составляющие: нормальную Fn к поверхности транспортирования и тангенциальную Ft . Нормальная составляющая прижимает частицу к поверхности транспортирования, обусловливая зависимость силы трения от положения частицы относительно магнитной системы. Тангенциальная составляющая в зависимости от конфигурации поля в данной точке направлена по ходу движения магнитных блоков, либо противоположно. В первом случае она вызывает ускорение движения частиц относительно неферромагнитного кожуха, на чем и основан процесс перемещения.Fn
и Ft достигают наибольших значений на краях магнитной системы, где высокие значения напряженности магнитного поля сочетаются с его неоднородностью. Понижение значений магнитной силы в центральной части системы обусловлено большей неоднородностью поля. Силу трения представим в видеF
тр = w (N + C) = w (Fn + mg + C),где
w - коэффициент сопротивления; N - нормальная реакция; m - масса частицы; С - сила сцепления частицы с неферромагнитным кожухом.Сила трения скольжения зависит от скорости относительного перемещения трущихся поверхностей. В рассматриваемом случае различие между силой трения покоя и силой трения движения учиты
вается путем введения различающихся коэффициентов сопротивления движению
w г и сопротивления покоя w п.Для решения дифференциального уравнения движения частицы в зоне действия магнитного блока характерные распределения составляющих магнитной силы линеаризованы на четырех участках возрастания и убывания. Зону действия соответственно направлению тангенциальной составляющей магнитной силы (по ходу движения магнитных блоков, либо против) можно разделить на две части: зону втягивания (участки I и II), где частице сообщается ускорение, направленное против магнитных блоков, и зону транспортирования (участки III и IV), где F
r обуславливает перемещение частиц по ходу магнитных блоков.Рассмотрим относительное движение частицы в системе координат, жестко связанной с магнитной системой.
Срыв частицы произойдет на участке I. Дифференциальное уравнение движения после срыва:
. (1)
Уравнение (1) после преобразований можно представить в следующей форме:
, (2)
где 
.
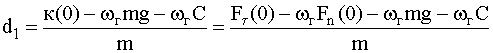Решение дифференциального уравнения (2)
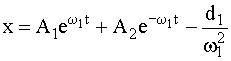. (3)
В момент времени t = t
1 частицы перейдут на участок II, при этом x(t1) = l1, где l1 - длина первого участка.Время t
1 определим, подставив x = l1 в выражение (3):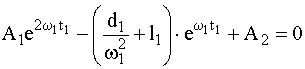 
. (4)
Уравнение (4) является квадратным относительно 
и имеет решение:
.
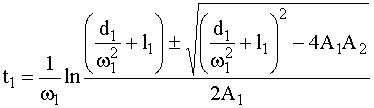Движение частицы на участке II описывается следующим дифференциальным уравнением:
, (5)
где 
Решение дифференциального уравнения (5) имеет вид:
.
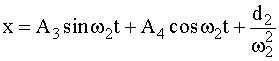Введем новую переменную Q(x):
Q(x) = F
t (x) - Fтр.д = K(x) - w гmg - w гС,причем Q(x) > 0 при Ft (x) > Fтр.д и Q(x) < 0 при Ft (x) < Fтр.д .
В первом случае скорость частицы растет, а во втором – замедляется. При Q(x) = 0 в момент времени t = t
2 разгон частицы прекратится, т.е.
и 
. Тогда 
.
В момент времени t = t
3 в точке с координатой
частица остановится относительно неподвижной системы координат, а в системе координат, жестко связанной с магнитной системой, 
.
Сравним величины пути разгона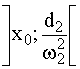 
и пути торможения 
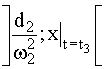, воспользовавшись равенством работ всех сил, действующих на частицу на этих отрезках, т.е. равенством соответствующих площадей, ограниченных графиком Q(x).
Отсутствие скачка силы трения соответствует максимальному пути разгона и торможения, при этом Q(x
0) = 0.Из условия равенства работ имеем:
,
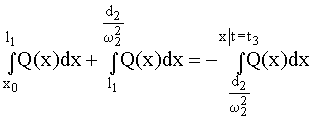причем для участка I: 
для участка II: 
где 
- угловые коэффициенты, характеризующие наклон прямых Q(x) соответственно на участке I и II.
После преобразования имеем:
.
Учитывая, что 
, имеем:
.
Таким образом, путь разгона частицы больше пути торможения.
Анализ магнитных систем показывает, что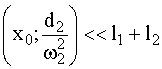 
Тогда получаем:
.
Таким образом, к моменту выхода на участок III частица будет иметь скорость относительно магнитных систем, равную V
0.На участках III и IV направление F
t совпадает с направлением V0. Дифференциальное уравнение движения частицы после срыва имеет вид: 
. (6)
В целях упрощения математических выкладок при описании движения частиц начало третьего участка примем за начало координат, а отсчет будем вести с момента срыва частицы.
Введем обозначение:
K(
e ) = Ft (e ) - w гFn(e ). (7)Зависимость K(
e ) в пределах участка III имеет вид:K(
e ) = K(0) + kкзe , (8)где kкз – положительный коэффициент, определяющий наклон прямой К(
e ) на участке III.С учетом (7) и (8) уравнение (6) приводится к виду:
,
где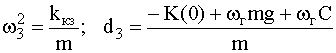 
Решение дифференциального уравнения имеет вид:
. (9)
После преобразований получим:
. (10)
Положив А
6 = LЧ sinb и А5 = LЧ cosb , имеем 
,
.
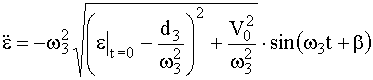В промежутке времени от t = 0 до t = t
1 (с учетом выбора нового начала отсчета), когда
становится равной нулю, e возрастает, т.е.
,
откуда 
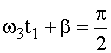и 
При t = t
1 
;
.
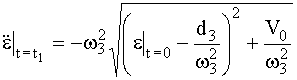При обратном ходе максимум скорости достигается при 
,
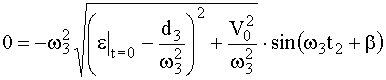откуда 
и 
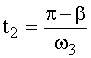
В этом случае
.
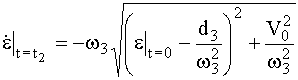Обратный ход частицы заканчивается при t = t
3, когда
, то есть
,
откуда
и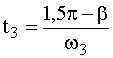 
.
В этом случае
;
.
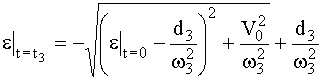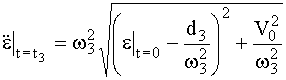Далее частица движется вправо.
В момент времени t = t
4 скорость частицы становится равной V0, т.е. в неподвижной системе координат частица останавливается.Тогда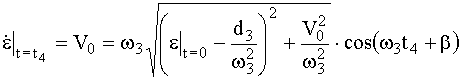 
откуда
и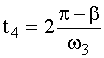 
,
и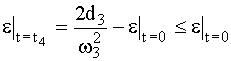 
,
учитывая, что 
Одиночная частица, удержанная в зоне действия магнитного блока, совершает автоколебания. Математически условие срыва частицы с неферромагнитного кожуха записывается следующим образом:
.
Решая неравенство относительно С, получим, что наличие наибольшей липкости груза Ссд, при которой его частицы еще будут проскальзывать по кожуху в зоне магнитного блока, существенно зависит от распределения по длине блока нормальной и тангенциальной составляющих магнитной силы и от коэффициента сопротивления
w n.