ИССЛЕДОВАНИЕ ПУСКОВЫХ РЕЖИМОВ ШАХТНЫХ ЛЕНТОЧНЫХ КОНВЕЙЕРОВ С УЧЕТОМ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ПРИВОДАХ

Кремешная А. А., магистрантка

E-mail: kremeshnaya@ukrtop.com

Abstract
Kremeshnaya A.A. Mining belt conveyors start-up regimes investigation with taking into account transitional processes in drives. The influence of transitional processes for belt conveyor start-up regime is reviewed in this article. And also there is proposed to transform mathematical model of engine with taking into account the belt conveyor as inconstant load.

В настоящее время с увеличением длины конвейеров и их производительности особое значение приобретают вопросы динамики пуска. Динамические процессы в ленточных конвейерах характеризуются появлением динамических натяжений, которые, алгебраически суммируясь со статическими, значительно увеличивают результирующие натяжения в конвейерной ленте и усилия в элементах конвейера. При пуске эти изменения могут привести к неустойчивой работе приводного барабана, например частичной или полной пробуксовке. Динамические усилия увеличивают нагрузки в механизмах натяжных устройств, в редукторе и других элементах конвейера и должны учитываться при их прочностном расчете.

Изучению пуска ленточного конвейера посвящено много работ, например работы [1,2], но они не учитывают переходные процессы, протекающие в приводе.

Ленточный конвейер и его привод находятся в тесном и сложном взаимодействии. Динамические процессы в двигателе влияют на процессы пуска и торможения ленточного конвейера. Но существует и обратная связь: являясь при динамических процессах переменной нагрузкой, конвейер оказывает влияние на пусковой процесс двигателя.

Динамические натяжения в ленте при нестационарном движении равны

Sдин = с1ρυ (t),

где υ(t) — скорость смещения сечения ленты (при пуске эта скорость совпадает по величине с текущей скоростью ленты); с1 - скорость распространения упругой волны; ρ – суммарная плотность соответствующей длины ленты [1].

Рассмотрим конвейер с грузовым натяжным устройством, расположенным в головной части. Дифференциальное уравнение движения привода

mпp dυ /dt + сгρгυ= F0 – W0 βДυ = ΔFβДυ;

(1)

приведенная к ободу барабана масса привода

mпp = k(GD)i /(gD).

где k — коэффициент, учитывающий инерцию редуктора, равный 1,2—1,3; βд— коэффициент, характеризующий наклон характеристики двигателя (рис. 1, прямые 1,2,3); βд=(F1 – F2 )/(υ1 - υ2); ΔF —избыточное по отношению к статическому сопротивлению движения усилие привода, равное F0 – W0 ; (GD)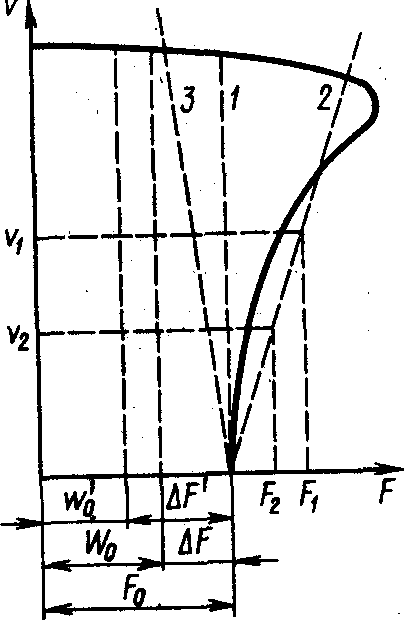— маховой момент ротора двигателя; ip — передаточное число редуктора; g—ускорение свободного падения; Dб— диаметр приводного барабана.

Рисунок 1- Механические характеристики привода<

Если двигатель имеет характеристику вида 1 (рис. 1), то βд=0; для характеристики 2 - β д>0; для характеристики 3 - βд<0.

Решение дифференциального уравнения (1) при начальном условии υ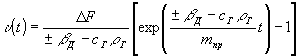0 при t = 0 имеет вид

.

Динамическое натяжение на набегающей ветви

Sдин.нб(t) = c ГρГ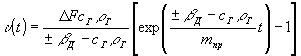

на сбегающей ветви в соответствии с граничными условиями Sсб = const, S дин.сб = 0.

В [3] предложено устройство и метод непрерывной регистрации статических и динамических механических характеристик, где датчиком момента служит ускориметр инерционного типа с угольными датчиками. Механическая характеристика, полученная в результате эксперимента, имеет вид представленный на рис.2.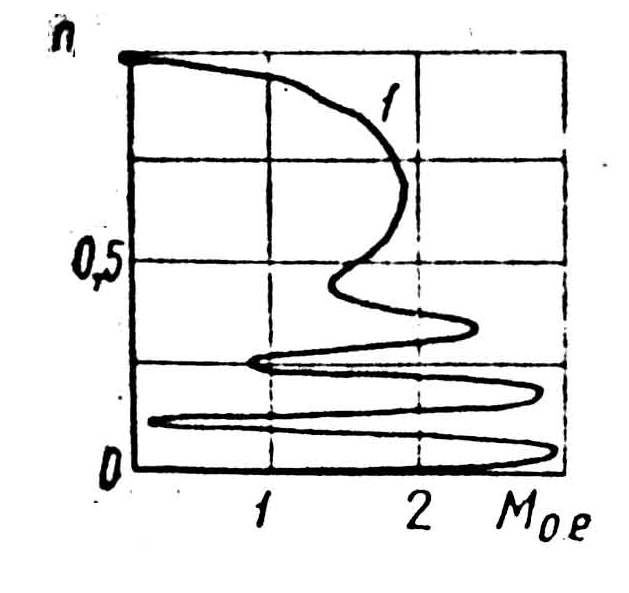

Рисунок 2 – Экспериментальная механическая характеристика асинхронной машины при пуске

Следовательно βд является переменной величиной при пуске и влияет на изменение величины динамического усилия.

Было проведено исследование пуска ленточного конвейера типа 1Л100К по методике, предложенной в [1]. Исходные данные:

длина конвейера L= 600м;

производительность Q=500т/час;

угол наклона β=0;

скорость движения ленты vн=3,15м /с;

распределенные линейные нагрузки от

ленты q л=245 Н/м;

вращающихся частей роликоопор

на верхней ветви qp' =110 Н/м;

на нижней ветви qp'' =55 Н/м;

ширина ленты В=1м;

коэффициенты сопротивления

для верхней ветви ωг'=0,03;

для нижней ветви ωп ''=0,04;

угол обхвата лентой приводных барабанов α=220°.

Результаты расчетов показали, что изменение βд от -200 до 200 Н·м/c приводят к изменению скорости ленты и динамического натяжения не более, чем на 0,5%.

Для определения времени разгона конвейера используется зависимость

,

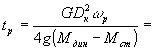
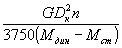где GDк2 – маховый момент конвейера; n – частота вращения; М ст- статический момент.

Динамический тормозной момент

,

(2)

где F дин – динамическое усилие; Rб – радиус барабана; υуст –скорость при установившемся режиме.

Исследование пусковых характеристик асинхронных двигателей при переменной нагрузке имеет большое значение, так как существенная неравномерность момента сопротивления приводит к особым условиям пуска.

В качестве математической модели двигателя при исследовании пусковых характеристик применена система уравнений (3).

Момент сопротивления нагрузки Мс задается функцией угла поворота. Система (3) справедлива для любого, сколь угодно сложного, закона изменения Мс.

 

;

;

;

(3)

;

;

,

где ; a ¢ s, a ¢ r – коэффициенты затухания статора и ротора; w 1 - скорость вращения ротора; ψ – потокосцепление; s — мгновенное скольжение двигателя, отн. ед.; γ — угол поворота ротора, рад; р – число пар полюсов; J— момент инерции вращающихся масс, кгм2, или дж • сек2 [4].

Для совместного решения системы уравнений (3), описывающей переходные процессы в электроприводе, и уравнения (2), описывающего динамические процессы, протекающие в тяговом органе ленточного конвейера, выполним преобразования.

Угловая скорость ротора

.

(4)

Угловая скорость барабана

.

(5)

Передаточное число редуктора

.

(6)

Из формулы (2), учитывая формулы (4-6), получим приведенный к ротору динамический момент сопротивления

,

(7)

.

(8)

Поскольку момент сопротивления в нашем случае является функцией времени, то число уравнений системы (3) сокращается до пяти, так как отпадает необходимость в определении угла поворота. Система дифференциальных уравнений (3) является нелинейной, поскольку содержит произведения искомых функций. Уравнения напряжений ротора содержат в правой части произведения составляющих потокосцеплений ротора на скольжение; уравнение движения включает в себя электромагнитный момент, зависящий от произведения потокосцеплений статора на потокосцепления ротора, и момент сопротивления, зависящий от времени.

Для решения системы начальные значения искомых функций выбираются соответствующими статической точке идеального холостого хода. Такой выбор при расчетах рабочих режимов очень удобен, так как для всех значений активного сопротивления ротора и нагрузки могут быть приняты одинаковые начальные условия. В рассматриваемой точке s=s нач=0. Принимаем потокосцепления равными нулю, записывая в правых частях первого и второго уравнений системы (3) составляющие неизменного напряжения. Таким образом, в начале решения мы рассматриваем переходные процессы, вызванные включением двигателя на соответствующее напряжение, а также переходные процессы, вызванные внезапным приложением нагрузки и переменной составляющей Мс.

Решение системы уравнений (3) с учетом уравнений (7,8) можно осуществить в пакете MatLab 5.3. Полученные результаты позволят уточнить основные параметры ленточного конвейера при пуске.

 

Перечень ссылок

  1. Шахмейстер Л.Г., Дмитриев В.Г. Теория и расчет ленточных конвейеров. – 2-е издание, переработано и дополнено – М.: Машиностроение, 1987, - 336с.

  2. Транспорт на горных предприятиях. Под общей редакцией проф. Кузнецова Б.А., М.: “Недра” 1976, 552с. Авт.: Кузнецов Б.А., РенгеничА.А., Штокман В.Г. и др.

  3. Шубенко В.А., Кирпичников В.М., Томашевский Н.И. Установка для экспериментальной записи статических и динамических характеристик асинхронных машин.// Изв.вузов. Горный журнал, №1, 1968.

  4. Асинхронные двигатели при периодической нагрузке. Артемюк Б.Т., Киев: “Техніка”, 1972, - 200с.