МЕТОДИКА РАСЧЕТА ТЕМПЕРАТУРЫ

 

С ИСПОЛЬЗОВАНИЕМ ИНДИВИДУАЛЬНЫХ ГРАДУИРОВОЧНЫХ ХАРАКТЕРИСТИК ПЛАТИНОВЫХ ТЕРМОМЕТРОВ.

Аннотация:

Рассмотрены вопросы  построения индивидуальной градуировочной шкалы платинового термометра  сопротивления по результатам измерения R0  и  R100   и проведена оценка точности расчета.  Представлен итерационный  алгоритм расчета температуры по измеренному сопротивлению термометра  Rt.

 

_{Как известно, ГОСТ 6651-94 ( Термопреобразователи сопротивления. Общие технические требования и методы испытаний) нормирует погрешность технических термометров сопротивления по классам точности А, В и С, определяя максимальную погрешность для каждого класса в зависимости от измеряемой температуры. При необходимости, повышение точности измерения температуры может быть достигнуто с помощью индивидуальной градуировки - измеренных значений R0 и R100. Однако, построение индивидуальной температурной шкалы термометра требует дополнительных расчетов.}

_{В ГОСТ 6651-94 приведены температурные зависимости относительного сопротивления W(t)=Rt/R0 для двух различных сортов платины (W100=1.391 и W100=1.385). Заметим, что величина W100 связана еще и с качеством отжига проволоки при изготовлении чувствительного элемента. Будем считать, что приведенные в ГОСТе зависимости точно соответствуют температурной шкале. Отклонения от приведенных зависимостей для конкретного чувствительного платинового элемента связаны только с отличием его R0 от номинального значения (50, 100 или 500 Ом) и отличием W100 от значения 1.391. Зависимости W(t) для различных сортов платины представляют собой семейство подобных кривых, по крайней мере, в интересующей нас области температур.}

_{Рассмотрим источники погрешности и их влияние на точность измерения.}

Погрешность определения температуры

П_{огрешность измерения температуры платиновыми термометрами сопротивления включает погрешность калибровки, временную нестабильность характеристик термометров и погрешность расчета температуры.}

_{Данные представлены выпускной лабораторией  «Термико».}

1. Калибровка термометра

_{Погрешность калибровки (определение R0, R100)состоит из:}

_{погрешности измерения сопротивления термометра dR=± 1*10-5   (dR=± 0.001 Ом для R=100 Ом, что соответствует D t=± 0.0025° С);}

_{погрешности образцового термометра D tобр=± 0.01° С;}

_{погрешности, вносимой ледяным термостатом D t0=± 0.0025° С;}

_{погрешности, вносимой стоградусным термостатом D t100=± 0.01° С.}

_{Таким образом:}

_{максимальная погрешность определения R0 составляет D R0=± 0.002 Ом (относительная d R0=± 2*10-5), или в температурном эквиваленте ± 0.005° С;}

_{максимальная погрешность определения R100 (с учетом погрешности температуры отнесения) составляет D R100=± 0.01 Ом (d R100=± 1*10-4 ), или в температурном эквиваленте ± 0.025° С;}

_{максимальная относительная погрешность определения W100=R100/R0 для термометра:}

d W₁₀₀=(D W₁₀₀)/W₁₀₀ =(D R₁₀₀)/R₁₀₀ +(D R₀)/R₀, или

d W₁₀₀=1*10^-4+2*10^-5=12*10^-5, _{тогдаабсолютная погрешность D W100» 0.0002.}

2. Стабильность термометрических характеристик

И_{сследования временной стабильности характеристик, проводившиеся в «Термико» на платиновых чувствительных элементах, отдельных платиновых термометрах, комплектах термометров в диапазоне температур до 200° С, а также результаты вторичной поверки термометров, поступающих от наших заказчиков показали, что практически все они подтверждают свой класс, определенный при калибровке.}

_{Применительно к термометрам это означает, что за 3 года эксплуатации они, по крайней мере, не изменяют характеристик более, чем на 0.02¸ 0.03° С}

_{Группа платиновых чувствительных элементов в составе поверочных устройств подвергалась ежедневному 5-кратному термоциклированию 0° С - 100° С. Изменение R0 за год составило при этом не более 0.003 Ом (~ 0.01° С).}

_{В качестве примера приводим результаты измерений R0t 4-х платиновых чувствительных элементов в процессе наработки при t=600° C (таблица 1) и 2-х термометров при t=200° C (таблица 2).}

Таблица 1

R0t/R0, ( R0 ном.=100 Ом) Наработка t ,час при t=600° C
0 час	200 час	440 час	536 час	616 час	1048 час
1.0	0.999953	0.999996	0.999981	0.999971	1.000009
1.0	0.999932	1.000017	1.000129	1.000209	1.000455
1.0	0.999703	0.999711	0.999687	0.999718	0.999731
1.0	0.999886	0.999889	0.999897	0.999961	1.0

Таблица 2

R0t/R0, ( R0 ном.=100 Ом) Наработка t ,час при t=200° C
0 час	100 час	208 час	426 час	734 час	1159 час
1.0	0.999910	0.999880	0.999880	0.999920	0.999930
1.0	0.999890	0.999900	0.999820	0.999870	0.999780

3. Расчет температуры

В ГОСТ 6651-94 приведены номинальные статические характеристики НСХ для платиновых термометров двух типов: для W₁₀₀=1.391 и W₁₀₀=1.385 в соответствии со шкалой МТШ-90. В интересующем нас диапазоне температур НСХ описывается интерполяционными уравнениями типа

W_t=1+At+Bt² (1), где:

Для W₁₀₀=1.391, A₁=3.9692*10^{-3 °} C^-1, B₁=-5.8290*10^{-7 °} C^-2;

Для W₁₀₀=1.385, A₂=3.9083*10^{-3 °} C^-1, B₂=-5.7750*10^{-7 °} C^-2.

Для определения А и В коэффициентов уравнений, описывающих НСХ термометров, имеющих значение W₁₀₀, отличающееся от приведенных в ГОСТе, необходимо использовать то, что отношение соответствующих коэффициентов для двух данных сортов платины с достаточной точностью совпадает с отношением значений их a из уравнения

R_t=R₀(1+a *t) (2):

a ₂/a ₁=0.00385/0.00391=0.98465; (1)

A₂/A₁=3.9083/3.9692=0.98465 (2); - отношения 1 и 2 равны между собой.

{(W₁₀₀)₂/( W₁₀₀)₁}²=(0.995686)² = 0.991391 (3)

B₂/B₁=5.7750/5.8290 = 0.990736; (4) отношения 3 и 4 совпадают с точностью 0,06%.

Таким образом, мы обходимся без дополнительных измерений для определения индивидуальной статической характеристики термометра, используя имеющиеся в нашем распоряжении калибровочные характеристики R0 и R100 , сохраняя при этом ГОСТовскую зависимость W(t), то есть не добавляя новых ошибок, связанных с аппроксимацией экспериментальных данных.

Итак, для реальной платины (1.392> W100> 1.385):

А=3.9692*10^-3*(a /0.00391) (5)

В=-5.8290*10^-7*{(W₁₀₀)/1.391}² (6)

С точностью, определяемой ошибкой измерения W100 мы можем составить интерполяционное уравнение (1) для платины, имеющей значение a (a=(W100-1)/100 - чувствительность термометра), отличающееся от стандартного 0.00391. Заметим, что экспериментальная ошибка определения (см. выше)

D W_{100 »} 0.2*10^-3 > 0.08*10^-3 (7)

Результаты измерения W100 в нашей практике, как правило, дает нормальное распределение значений с максимумом при 1.3912¸ 1.3914.

4. Алгоритм расчета температуры

Расчет температуры по уравнению (1), которое описывает индивидуальную НСХ термометра с учетом калибровочных характеристик R_o и R₁₀₀,осуществляется итерационным методом по алгоритму:

Определяется значение W_изм=R_изм/R_o. (R_изм – измеренное значение сопротивления термометра при данной температуре, R_o –сопротивление термометра при 0^oС).

Измеренное значение W_изм сравнивается с W_рас, рассчитанным по температуре t_рас, полученной в предыдущем приближении (или по стартовому значению, например 100^оС ). Определяется поправка D t= (W_рас–W_изм)/a  ( a=(W100-1)/100 - чувствительность термометра), которая вычитается из t_рас: t_изм= t_рас-D t. При выполнении условия |D t|< К расчет заканчивается (К-критерий точности расчета). При К=0.001 требуется 2-3 приближения в том случае, если стартовое значение t_рас значительно отличается от измеряемого.

Если расчет температуры ведется по индивидуальной шкале термометра, то погрешность измерения температуры состоит из погрешности градуировки, плюс  погрешность измерения сопротивления,  плюс погрешность, связанная с условиями применения термометра.

 

Погрешность определения разности температур

Аннотация:

Проведен анализ погрешности измерения разности температур разностными комплектами термометров КТПТР. Сравнение с требованиями Европейского стандарта EN 1434

Измерения разности температур D t при помощи комплектов термометров КТПТР, кроме погрешности измерения температуры d t, характеризуются величиной погрешности определения разности температур d (D t).

Разностные комплекты термометров КТПТР составляются путем подбора пар термометров по результатам измерения R₀ и R₁₀₀. Разность показаний подобранных в пару термометров при  температурах 0^оС и 100^оС не превышает 0.1^оС. По результатам статистических исследований  около 2000 комплектов различных типов КТПТР установлено, что, с вероятностью 95%, показания  пары термометров комплекта в температурных точках 0^оС и 100^оС различаются не более, чем на   0,075^оС.  На диаграмме показано распределение относительного числа   комплектов  в зависимости от  разности показаний dT   термометров  комплекта при температуре 100 оС.  

 

 

 

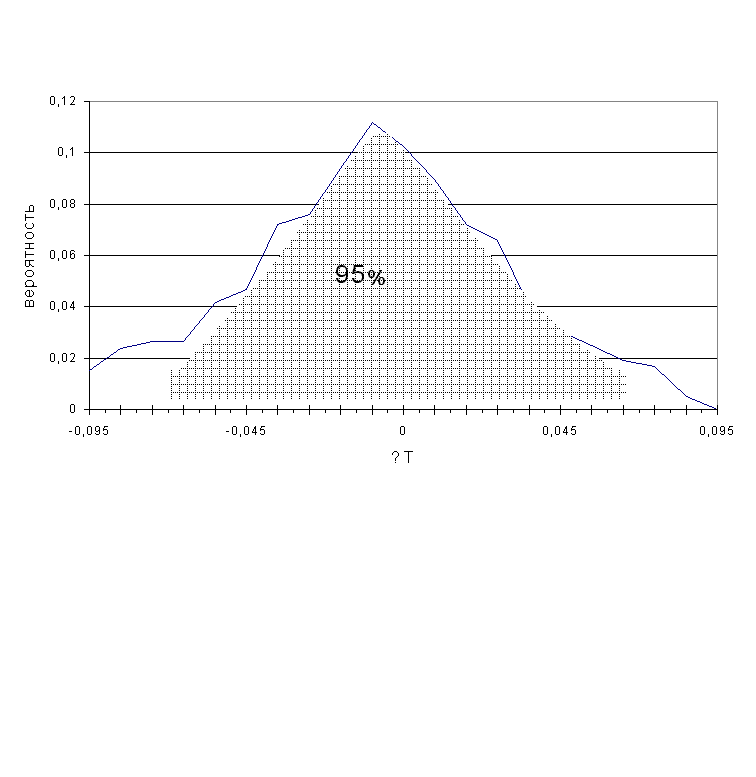
Рассмотрим диаграмму:

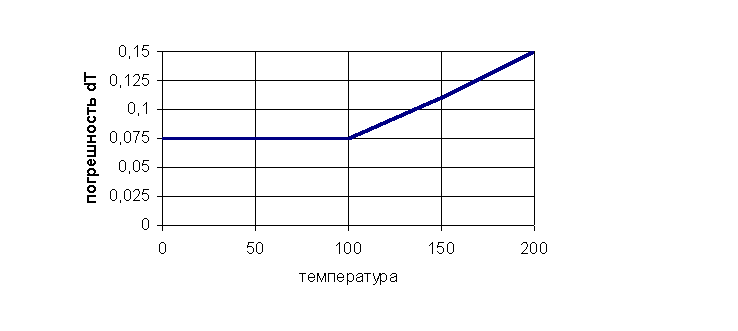
На диаграмме изображена зависимость максимальной    погрешности   (доверительная вероятность 95%)   определения разности температур от температуры "горячего" термометра.    Граница области допустимых погрешностей достаточно хорошо описывается параболой:

d(dT) = 0.076 – 2.7*10^-4*T + 3.2*10^-6*T², ^оС, (8)

где t – показания "горячего"  термометра.

В таблице 3 приведены значения наиболее вероятных (доверительная вероятность 95%) значений максимальной погрешности и максимально допустимой погрешности для различных температур . 

Таблица 3.

t1,oC	d (D t),oC (95%)	d (D t),oC мах
0	0.075	0.10
100	0.075	0.10
150	0.11	0.15
200	0.15	0.20

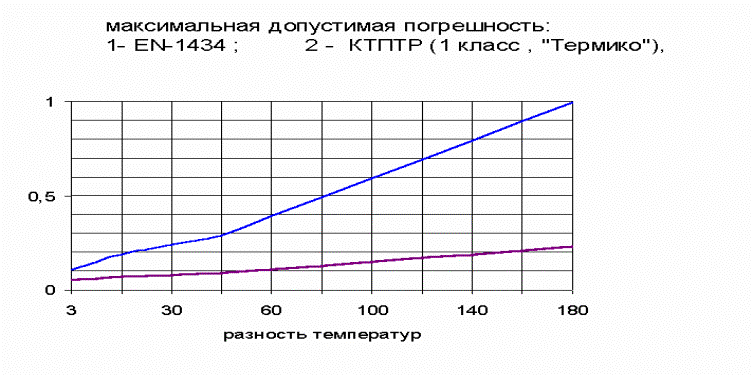
В заключение приведу графики допустимых погрешностей d (D t) комплектов по Техническим Условиям «Термико» и те же требования Европейского стандарта EN 1434. При этом Технические Условия «Термико» не учитывают зависимость погрешности определения D t от значений температуры t1 и t2, измеряемых термометрами комплекта. В стандарте EN 1434 эта зависимость явно не выражена. Возможно, она учтена путем обеспечения гарантированного запаса максимально допустимой погрешности. Однако, допуск на максимальную погрешность EN 1434 в пять раз больше, чем принято в "Термико".

 

 

 

 

 

 

 

 

 

 

Моделирование тепловых процессов при измерениях температуры

Аннотация:

Предложен метод математического моделирования развития во времени  процесса установления   теплового равновесия в системе  термометр сопротивления - объект измерения.  Рассчитывается распределение температур  по конструкции термометра  в любой момент времени, определяется показатель тепловой инерции термометра, дополнительная статическая погрешность измерения температуры в зависимости от способа контакта термометра с объектом измерения.  Предложены рекомендации по доработке методики  поверки термометров в условиях, отличающихся от рабочих условий применения.  Получено совпадение    расчетных данных с  результатами измерений.

 

Главным критерием качества при измерении температуры объекта является  наличие теплового равновесия между термометром и объектом. Однако,  тепловое  равновесие вовсе не гарантирует  равенства температур термометра и объекта, поскольку всегда существует тепловой поток, проходящий через термометр  от объекта в окружающую среду, который создает определенный перепад  между температурой объекта и  температурой чувствительного элемента  ( ЧЭ ). Любой термометр имеет тепловую связь  с окружающей средой через собственную арматуру и выводящие провода.  Этот перепад температур представляет собой  дополнительную погрешность измерения, величина которой определяется отношением теплового сопротивления между объектом  и  ЧЭ  к  тепловому сопротивлению между   ЧЭ   и окружающей средой. 

Настоящая  работа посвящена  оценке  дополнительной погрешности измерения температуры  техническими термометрами сопротивления, связанной с условиями теплообмена между термометром и объектом измерения.

При выборе минимальной глубины погружения  Lmin,   обеспечивающей  заданный уровень точности измерения температуры объекта,   необходимо  учитывать  характер теплообмена термометра с  измеряемой средой.  Поскольку в большинстве  случаев рабочей средой является водяной поток, а поверочные термостаты в качестве рабочей жидкости используют перемешиваемое силиконовое масло, то различие физических условий в рабочих условиях и при поверке    приводит к заметной разнице в результатах измерений при одинаковой глубине погружения.   Особенно это существенно для термометров, у которых  монтажная длина не намного больше длины чувствительного элемента.

Обычно для оценки  минимально необходимой глубины погружения   Lmin  используются эмпирические соотношения типа  Lmin>n*d, где  d - диаметр термометра, а число   n   (от 10 до 30)   выбирается в зависимости от условий применения. Очевидно, что такая оценка может дать самые приблизительные результаты, поскольку при этом не учитывается влияние на  теплообмен особенностей конкретной конструкции термометра, таких как  толщина стенок корпуса термометра, теплопередача по выводящим проводам и.т.д.,  что, конечно, ведет к неверной оценке   Lmin.

Наилучшим способом   априори   оценить качество взаимодействие термометра с объектом измерения является математическое моделирование тепловых процессов.

Рассчитать распределение температуры по термометру,   путем решения дифференциальных уравнений  теплопередачи невозможно,   поскольку конструкция любого термометра содержит  границы раздела между элементами с различными физическими свойствами,   что исключает необходимую для решения неразрывность функций и производных.   Остается численное моделирование, состоящее том, что объект исследования заменяется системой, состоящей из  большого числа достаточно малых элементов, в пределах которых теплофизические свойства сохраняют однородность.   Для каждого элемента определяется теплоемкость   Cр(t).   Тепловые связи между элементами рассчитываются как тепловые сопротивления, определяемые свойствами материалов и геометрией конструкции.   Далее, для каждого элемента объекта составляется уравнение теплового баланса: 

количество тепла, поглощенное элементом за время   tau  должно быть равно алгебраической сумме тепловых потоков, прошедших через элемент за то же время  -   Ср×dt=Sum(Qi)×tau, где Ср - теплоемкость элемента,   dt оС - величина нагрева,   tau,с - шаг расчета по времени,    Qi, Вт - мощность теплового потока вдоль i-той тепловой связи.

Стартовое распределение температуры в системе    "термометр-объект"  выбирается таким же, как при измерении инерционности термометра   ( tтерм = idem   <<  tобъект = idem ),  с тем,   чтобы в качестве объективного контрольного параметра в процессе расчета получить еще и  показатель тепловой инерции   "kинерц", значение которого легко может быть измерено экспериментально    (ГОСТ Р 50353-92). Кроме того, Показатель термической инерции "kинерц",

Поскольку термометр обладает, как правило,  цилиндрической симметрией, то  элементы разбиения определяются как однородные кольцевые участки высотой   dx  (dx = 1 мм).   Теплообмен с жидкой средой рассчитывается при скорости движения жидкости   ~0,1 м/с  (типичное значение  для термостатов).   Теплообмен на участке вне термостата рассчитывается по модели свободной конвекции воздуха.   Температурные зависимости теплофизических свойств рабочих веществ и материалов  получены из справочной литературы, за исключением теплопроводности корундового порошка    (размер зерна~40 мкм),   для определения которой были проведены специальные экспериментальные исследования.

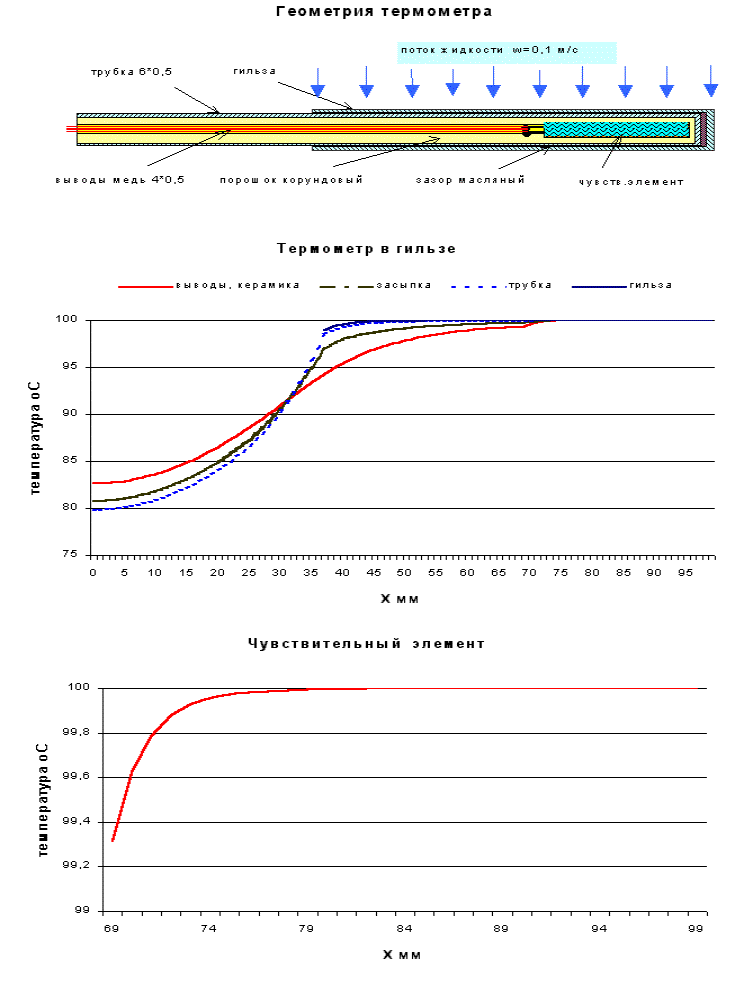
На диаграммах  представлены результаты расчета для термометра   ТПТ-15   (использующегося в разностных комплектах КТПТР-04)   с монтажной длиной    Lм = 65 мм  в защитной гильзе  (начальная температура 20 оС),  погруженного в воду с температурой 100 оС. Температура окружающего воздуха - 20 оС.   Линии на графиках соответствуют распределению температуры по отдельным частям конструкции - выводящим проводам, засыпке из корундового порошка,  трубке и  гильзе, чувствительному элементу.   Рассчитанный показатель термической инерции в воде  kинерц=10 с не отличается от измеренного  более,  чем на 1 с.   После достижения теплового равновесия среднеинтегральная  температура чувствительного элемента равна   99,958 оС.   То есть,  при данной конфигурации  дополнительная ошибка измерения составляет   0,042 оС.

 

 

В таблице 1  представлены результаты расчета для того же термометра в различных условиях применения,  при температуре измеряемой среды   100  оС.

Таблица 1

Измеряемая среда	Глубина погружения Lп, мм	kинерц, с	Измеренная температура,t оС	дополнительная ошибка измерения, Δt оС
масло ПМС100	65	16	99,870	0,13
масло ПМС100,	85	16	99,985	0,015
вода	65	6,5	99,962	0,038
вода	75	6,5	99,988	0,012
вода, (в гильзе)	65	10	99,958	0,042

Из таблицы следует, что для данного термометра глубина погружения    Lп =  Lм = 65 мм является минимально допустимой при погружении в воду, ошибка не превышает 0,038 оС   (при установке в гильзу - 0,042 оС).  Однако,  при поверке,  при измерении температуры силиконового масла   ПМС100,   которое применяется обычно в качестве рабочей жидкости в поверочных термостатах, глубина погружения должна быть увеличена на ~20 мм,    (Lп=Lм+20 мм).  Это позволит  избежать дополнительной погрешности,   возникающей из-за ухудшения теплообмена между термометром и маслом, более вязким по сравнению с водой.   Очевидно, минимальная глубина погружения должна увеличиваться с увеличением вязкости измеряемой среды.

Из приведенных результатов следует, что методика поверки    ( МП )   для конкретного типа термометра должна, помимо прочего,   содержать сведения  о минимальной глубине погружения в различных рабочих жидкостях с учетом различия их физических свойств  (в основном, вязкости).   При этом минимально допустимая  глубина погружения     Lmin  при поверке в масляном термостате может оказаться больше монтажной длины термометра   Lм .

Задача теплообмена между термометром и термостатом в случае  т. н. "сухого" термостата,   в котором тепловой контакт осуществляется теплопроводностью воздушного или жидкостного зазора между термометром и установочным гнездом термостата, решается аналогичным способом.   Результат при этом аналогичен результату  решения  для термометра, помещенного в гильзу, выполненную из того же материала, что и установочное гнездо термостата.   Однако,  минимально необходимая глубина погружения  существенно увеличится.   Величина зазора между термометром и гильзой также пропорционально увеличивает дополнительную погрешность измерения температуры. 

 В таблице 2 представлены результаты расчета равновесной температуры  чувствительного элемента и дополнительной погрешности Δt оС, а также  показателя термической инерции  "kинерц".   для двух значений глубины погружения  Lп =65 мм  и Lп =80 мм  в медной гильзе с различными величинами зазора    между гильзой и корпусом термометра.   Температура термостата   100 оС, окружающей среды  - 20 оС.

Таблица 2

зазор b=(dг - dт )/2, мм	Lп = 65 мм		Lп =80 мм		kинерц ,с
	t оС	Δt оС	t оС	Δt оС	Lм = 65 мм	Lм =80 мм
0,01	99,96	0,04	99.987	0,013	6,9	6,9
0,05	99,952	0,048	99,985	0,015	8,3	8,3
0,1	99,941	0,059	99,981	0,019	10,0	10,0
0,15	99,930	0,07	99,976	0,024	11,7	11,7
0,2	99,917	0,083	99,971	0,029	13,4	13,4

Сравнение результатов показывает, что при большей глубине погружения    величина зазора меньше влияет на точность измерения, а значение  Lп =80 мм  достаточно для технических термометров. Показатель термической инерции kинерц   не изменился, поскольку не изменился  диаметр сечения термометра.