УДК 681.326
Ю.Е. Зинченко
Т-МОДЕЛЬ ДИСКРЕТНОГО УСТРОЙСТВА И РЕШЕНИЕ ДИАГНОСТИЧЕСКИХ ЗАДАЧ НА ЕЕ ОСНОВЕ
К началу 80-х годов несостоятельность классического подхода проектирования вычислительной техники (ВТ), когда диагностическое обеспечение (ДО) разрабатывается на последних этапах, уже ни у кого не вызывала сомнений. Как результат разрешения конфликта родилось новое направление - контролепригодное проектирование (design for testability) [1-4]. Развитие этого направления привело к появлению стандарта IEEE Std. 1149.1 (Boundary-Scan), разработанного объединенной группой по тестам - JTAG, который периодически обновляется [5]. Однако, несмотря на полученные вслед за эти важные результаты, по-прежнему остается доминирующим традиционный подход тестового диагностирования (ТД), состоящего в применении для каждой из его задач индивидуального подхода, начиная от идеи и заканчивая технической реализацией. Это приводит к высокой трудоемкости и стоимости ДО. В то же время общая природа задач ТД создает почву для унифицированного подхода. Стремительное развитие новейших HDL- и FPGA-технологий и САПР на их основе [6,7] создают почву для разработки такого подхода на их основе.
В статье приводятся общие принципы построения диагностической модели ДУ и решения разнородных задач детерминированного и случайного тестирования единым подходом на основе имитационного моделирования с возможностью аппаратной реализации на FPGA.
1. Т-модель дискретного устройства
Основой предлагаемого подхода является так называемая Т-модель объекта диагностики (ОД).
В общем случае ОД дискретного типа со множеством входов X={xi}, i=1,..,n, выходов Y={yj}, j=1,...,m, множеством моделируемых неисправностей H={hk}, k=1,...,p и его Т-модель можно представить обобщенными структурами:
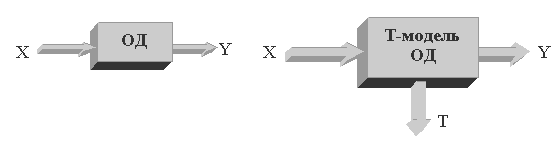
Рис.1 - Дискретный ОД и его Т-модель
Особенностью Т-модели является наличие специальных выходов Т={Tk}, называемых выходами тестируемости неисправностей ОД. Выход Tk выражает условие обнаружения неисправности hk входной тестовой последовательностью на выходах Y и может быть описан функцией тестируемости неисправности T(hk), которая в общем случае определяется над входами и внутренним состоянием ОД.
Если в качестве ОД выступает комбинационная логическая схема (КЛС), то функция T(hk) для неисправности hk константного типа (КН),Т(hk)=CO(hk)&O(Kк) , ( 1 )
где CO(hk) - функция управляемости неисправности hk; O(hk) - функция наблюдаемости контрольной точки k , в которой моделируется hk.Функция управляемости выражает условие проявления неисправности в месте ее возникновения и определяется в зависимости от типа как прямая либо инверсная функция fк(Х), реализуемая схемой в исправном состоянии в КТ k :
 , ( 2 )
, ( 2 )
Функция наблюдаемости выражает условие проявления (наблюдаемости) состояния контрольной точки k на внешних выходах ОД. Формально она обычно выражается с помощью булевой производной [8,9]:
 ,( 3 )
,( 3 )
Так как число всевозможных КН пропорционально кубу вентилей ОД [8-11], а схема, реализующая функцию тестируемости для отдельных неисправностей, может быть соизмеримой по сложности с самим ОД , то тривиальная реализация Т-модели по указанным функциям оказывается проблематичной. При этом реализация функции управляемости не представляет затруднений - это прямой либо инверсный выход структурного элемента ОД, реализующего функцию fк ; проблематичной оказывается реализация функций наблюдаемости как по сложности так и по точности [9,12].
Функция наблюдаемости некоторой КТ k представляется в данной работе суперпозицией так называемых локальных функций тестируемости (ЛФТ). ![]()
 ,
,
 , ( 4 )
, ( 4 )
. . . ,
 .
.
Тогда наблюдаемость КТ k можно представить суперпозицией ЛФН ОД:
![]() , ( 5 )
, ( 5 )
Логико-топологический анализ ДУ позволяет минимизировать необходимое число ЛФН, что в конечном итоге существенно упрощает реализацию функций наблюдаемости КТ ОД.
Построение Т-модели, предлагаемый в данной работе, состоит в том, что для каждого выхода тестируемости Тk строится так называемая распределенная логическая схема тестируемости, которая реализует на своем выходе Тк функцию вида (1), где функция наблюдаемости строится как суперпозиция ЛФН, минимизированных на основе логико-топологического анализа ОД.
Построение Т-модели для последовательностной схемы (ПС) выполняется на основе модели Хаффмана. Как известно, модель Хаффмана любое ДУ представляет композицией КЛС и элементов задержки (ЭЗ), включенных в обратную связь КЛС [3,4]. Логически разорвав обратные связи:
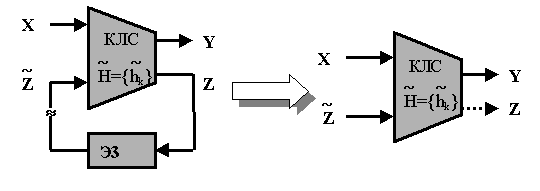
Рис.2 - Преобразование ПС по модели Хаффмана
2. Связность и минимизация константных неисправностей
Основным недостатком Т-модели является ее сложность, обусловленная большим количеством моделируемых неисправностей. Поэтому построение модели не представляется эффективным без учета связности неисправностей. Задачу определения связности неисправностей, в том числе для неисправностей константного типа, относят к задачам более сложным, чем синтез теста, поэтому на практике обычно ограничиваются простыми случаями эквивалентности и доминирования неисправностей [3,4]. Однако предлагаемая Т-модель обладает возможностью определения всевозможных видов связности КН, что позволяет, во-первых, упростить саму модель и, во-вторых, снизить вычислительные затраты при решении конкретных диагностических задач.
Пусть имеются КН h1 и h2 с множествами тестов R1 и R2 , построенных путем решения уравнений тестируемости для этих неисправностей вида T(hk)=1, t(h1)Î R1 , t(h2)Î R2 . Возможны следующие варианты соотношения этих множеств.
-
 . Неисправности h1 и h2 в этом случае будем называть несовместными и обозначать как h1ќh2.
. Неисправности h1 и h2 в этом случае будем называть несовместными и обозначать как h1ќh2. - R1 = R2 - этот случай соответствует эквивалентности неисправностей: h1~h2.
- R1 Ì R2 , но
 , но R1 Ë
R2, и
, но R1 Ë
R2, и 
- Если h1ќh2 , то T(h1)&T(h2)=0 на всем диапазоне входных воздействий и тест одной неисправности никогда не является тестом для другой: t(h1) ¹ t(h2).
- Если h1~h2, то T(h1)&T(h2)=1 на любой входной комбинации и тест одной неисправности всегда является тестом для другой: t(h1)=t(h2).
- Если h1→h2, то
 T(h1)&T(h2)=1 и
T(h1)&T(h2)=1 и  , на котором
, на котором  (h1)&T(h2)=1, т. е тест доминирующей неисправности всегда является тестом и для подчиненной неисправности; обратное утверждение не всегда верно.
(h1)&T(h2)=1, т. е тест доминирующей неисправности всегда является тестом и для подчиненной неисправности; обратное утверждение не всегда верно. - Если h1&h2, то
 , т.е. существует тест, совместный для обеих неисправностей, а также
, т.е. существует тест, совместный для обеих неисправностей, а также  и
и  , на которых
, на которых  (h1)&T(h2)=1 и T(h1)&
(h1)&T(h2)=1 и T(h1)&
Приведенные соотношения функций тестируемости могут служить основой для определения различных видов связности КН ОД на базе Т-модели. Схема моделирования для решения такой задачи приведена на рис. 4,а. Анализатор связности путем моделирования схемы на случайных тестовых воздействиях выполняет анализ функций тестируемости для всевозможных пар КН по приведенным выше соотношениям , что позволяет определять точно либо с достаточно высокой вероятностью всевозможные виды связности КН ОД.
3. Решение диагностических задач на основе Т-модели ОД
Принцип решения диагностических задач на базе Т-модели отображается структурной схемой, представленной на рис. 3. Такая схема кроме собственно Т-модели включает в свой состав Т-оболочку, функции и схема которой определяется типом решаемой задачи. Используемый в структуре генератор случайных либо псевдослучайных тестов (ГСТ) используется для возбуждения функций тестируемости по случайному (псевдослучайному) закону. В дальнейшем условимся, говоря о случайном тесте либо генераторе иметь ввиду также и псевдослучайные их разновидности. Под воздействием теста на выходах тестируемости {Т(hk)} появляется тестовая реакция, так что если в некоторый момент времени t на входах ОД генератор тестов выставляет тест неисправности hk, то соответствующий выход тестируемости взводится в лог."1"; в противном случае на этом выходе лог. "0". Тестовая реакция поступает на Т-оболочку, специфическую для каждой задачи, которая на своем выходе ![]() выставляет результат решения задачи.
выставляет результат решения задачи.
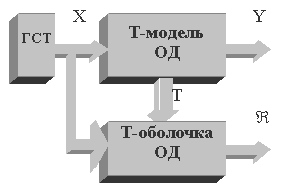
Рис. 3 Принцип решения диагностических задач на базе Т-модели
Спектр задач, которые могут быть решены представленным подходом, может быть достаточно широк. Авторами данной работы предлагаются способы решения следующих диагностических задач.
Моделирование КН и анализ полноты теста.
Схема моделирования для решения этой задачи приведена на рис. 4,б. В качестве Т-оболочки в данном случае выступает регистр RG, основная задача которого состоит в фиксации лог."1" в разрядах, соответствующих выходам тестируемости ОД хотя бы в одном такте моделирования, что говорит о факте обнаружения КН заданным тестом Тзд .
Синтез детерминированного теста для отдельной КН и ОД в целом [3,4,8,9,11].
Также как и при эвристическом алгоритме [4] здесь используется ГСТ. Т-оболочка - анализатор тестов - выполняет задачу обнаружения тестовых векторов и сохранения их в ОЗУ тестов. При обнаружении очередного теста некоторой КН анализатор тестов определяет также и те КН, которые тестируются совместно и "удаляются из списка" необнаруженных неисправностей. Моделирование производится до "обнуления" указанного списка либо до достижения определенного временного предела (см. рис. 4,г).
Определение вероятностных показателей тестируемости КН и труднотестируемой КН [4,12,13].
Эта задача решается путем подсчета счетчиками-регистрами (СТRG), образующими в данном случае Т-оболочку, числа лог. "1" на выходах Т-модели, соответствующих вероятностям тестируемости КН -{q(hк)}. Далее определяется "наихудшая неисправность" по минимальной величине : qt=min{q(hк)}. Зная qt можно построить зависимость длины (N) случайного теста от вероятности обнаружения неисправностей (Q) по концепции "наихудшей неисправности" [4]: N=log(1-Q)/log(1-qt) (см. рис. 4,в).
Определение среднестатистической КН.[4].
Под среднестатистической подразумевается КН hср с тестируемостью qср, рассчитываемая как среднеарифметическая величина среди вероятностей тестируемости всех неисправностей ОД:  . Способ вычисления qср, предлагаемый в данной работе, можно представить структурой, приведенной на рис. 4,д. Отличие от вышеописанной задачи состоит в Т-оболочке и модифицированной под данную задачу модели ОД, которая содержит так называемые "суммарные" выводы тестируемости КН - {sk} и называется S-моделью. В качестве Т-оболочки выступает
. Способ вычисления qср, предлагаемый в данной работе, можно представить структурой, приведенной на рис. 4,д. Отличие от вышеописанной задачи состоит в Т-оболочке и модифицированной под данную задачу модели ОД, которая содержит так называемые "суммарные" выводы тестируемости КН - {sk} и называется S-моделью. В качестве Т-оболочки выступает
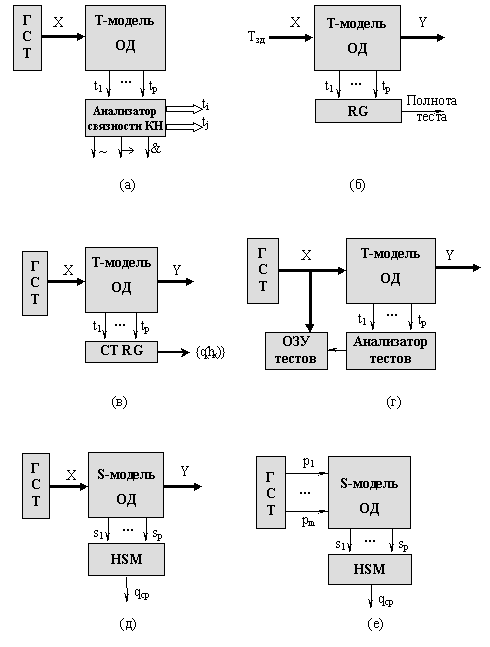
Рис.4 Способы решения диагностических задач
Оптимизация случайного и псевдослучайного теста [3,8,9].
Под оптимизацией случайного теста ДУ обычно подразумевается задача обеспечения максимальной обнаруживающей способности при фиксированной длине теста либо, наоборот, минимизацию длины теста, обеспечивающего заданную обнаруживающую способность. Обе эти задачи сводятся к подбору оптимального набора вероятностей сигналов теста путем моделирования. Предлагаемый способ подобен эвристичес-кому алгоритму, сводящемуся к последовательному подбору значений вероятностей сигналов на входах ОД [3,8,9], однако в отличие от последнего обладает большей эффективностью за счет распараллеливания процессов моделирования КН и возможностью аппаратной реализации. Способ можно представить схемой моделирования, приведенной на рис.4,е. В качестве критерия оптимизации используется вероятность тестируемости ОД qср , которая для каждого набора входных вероятностей (p1,:, pn) определяется аналогично ранее описанной задачи.
При построении Т-оболочек для каждой диагностической задачи используются таблицы связности КН, что позволяет оптимизировать их структуру, а также снизить время и трудоемкость решения задач. Экспериментальные исследования, выполненные в системе ACTIVE-HDL, фирмы ALDEC, Inc, [6] с использованием языка описания аппаратуры VHDL, показали, что предложенный подход решения диагностических задач характеризует-ся высоким быстродействие, низкой трудоемкостью и высокой степенью автоматизации за счет единого подхода решения разнообразных диагностических задач, а также возможностью аппаратной реализации. Наибольшая эффективность данного подхода обеспечивается в случае реализации рассмотренных моделирующих схем в виде тест-процессора, выполняемого на базе FPGA и CPLD [7], что обеспечивает параллельное аппаратное моделирование всех КН ОД.- Берглунд А.П. Проверка кристаллов, плат и системы в целом методом сквозного сдвигового регистра // Электроника, 1979 - ї 1. -С. 35-39.
- Уильямс Т.У., Паркер К.И. Проектирование контролепригодных устройств //ТИИЭР, 1983. - Т. 71. - ї 1. - С. 122 - 139.
- Williams T.W., Parker K.P. Design for testability //IEEE Trans. Comput., 1982 - ї1.- p.2-14.
- Abramovici M. Digital System Testing & Design. - IEEE, 1990. - 570 p.
- Test access Port and Boundary-Scan Architecture //IEEE Standart 1149.1 - 1990 (Includes IEEE Standart 1149.1a - 1993).
- ACTIVE-HDL Серия. Книги 1-4. США, Невада: ALDEC, Май 1999 (www.aldec.com.ua).
- Программируемые логические ИМС на К-МОП структурах и их приме-нение /П.П. Мальцев, Н.И. Гарбузов, А.П. и др. - М.: Энергоатомиздат, 1998.- 160 с.
- Ярмолик В.Н. Контроль и диагностика цифровых узлов ЭВМ. - Мн.: Наука и техника. 1988, - 240 с.
- Барашко А.С., Скобцов Ю.А. и др. Моделирование и тестирование дискретных устройств. - Киев: Наук. думка, 1992.- 288с.
- Горяшко А.П. Синтез диагностируемых схем вычислительных устройств. - М.: Наука, 1987. - 288 с.
- Хаханов В.И. Техническая диагностика цифровых и микропроцессорных структур. - K: ИСИО, 1995.- 242с.
- Тарасенко А.Н. Методы оценки и показатели тестируемости дискретных устройств (обзор) //Зарубежная радиоэлектроника, 1989, ї 7. - C. 24-29.
- Беннетс Р. Проектирование тестопригодных логических схем /Пер. с английского. - М.: Радио и связь, 1990 - 176с.