Как Вы уже знаете, существуют задачи, для которых доказано отсутствие общего алгоритма решения (например, задача о разрешимости Диофантова множества). В то же время, можно сказать, что, если бы мы обладали бесконечным запасом времени и соответствующими ресурсами, то мы могли бы найти решение любой задачи. Здесь имеется в виду не конструирование нового знания на основании имеющегося (вывод новых теорем из аксиом и уже выведенных теорем), а, прежде всего, "тупой" перебор вариантов.
Еще в XVII столетии великий Лейбниц пытался раскрыть тайну "Всеобщего Искусства Изобретения". Он утверждал, что одной из двух частей этого искусства является комбинаторика - перебор постепенно усложняющихся комбинаций исходных данных. Второй частью является эвристика - свойство догадки человека. И сейчас вторая часть Искусства Изобретения все еще остается нераскрытой. На языке нашего времени эта часть - модель мышления человека, включающая в себя процессы генерации эвристик (догадок, изобретений, открытий).
Однако прежде чем перейти к рассмотрению улучшенных переборных алгоритмов (улучшенных потому, что для простого перебора у нас в запасе нет вечности), я бы отметил еще один универсальный метод ускорения перебора - быстрое отсечение ложных (или вероятно ложных, что и используется большинством алгоритмов) ветвей перебора.
Прежде всего, упомяну, что отнюдь не все ученые признают наличие эволюции. Многие религиозные течения (например, свидетели Иеговы) считают учение об эволюции живой природы ошибочным. Я не хочу сейчас вдаваться в полемику относительно доказательств за и против по одной простой причине. Даже, если я не прав в своих взглядах, объясняя эволюционные алгоритмы как аналоги процессов, происходящих в живой природе, никто не сможет сказать, что эти алгоритмы неверны. Несмотря ни на что, они находят огромное применение в современной науке и технике, и показывают подчас просто поразительные результаты.
Основные принципы эволюционной теории заложил Чарльз Дарвин в своей самой революционной работе - "Происхождение видов". Самым важным его выводом был вывод об основной направляющей силе эволюции - ею признавался естественный отбор. Другими словами - выживает сильнейший (в широком смысле этого слова). Забегая вперед, замечу, что любой эволюционный алгоритм имеет такой шаг, как выделение самых сильных (полезных) особей. Вторым, не менее важным выводом Дарвина был вывод об изменчивости организмов. Аналогом данного закона у всех алгоритмов является шаг генерации новых экземпляров искомых объектов (решений, структур, особей, алгоритмов).
Именно отбор наилучших объектов является ключевой эвристикой всех эволюционных методов, позволяющих зачастую уменьшить время поиска решения на несколько порядков по сравнению со случайным поиском. Если попытаться выразить эту эвристику на естественном языке, то получим: сложно получить самое лучшее решение, модифицируя плохое. Скорее всего, оно получится из нескольких лучших на данный момент.
Из основных особенностей эволюционных алгоритмов можно отметить их некоторую сложность в плане настройки основных параметров (вырождение, либо неустойчивость решения). Поэтому, экспериментируя с ними, и получив не очень хорошие результаты, попробуйте не объявлять сразу алгоритм неподходящим, а попытаться опробовать его при других настройках. Данный недостаток следует из основной эвристики - можно "уничтожить" предка самого лучшего решения, если сделать селекцию слишком "жесткой" (не зря ведь биологам давно известно, что если осталось меньше десятка особей исчезающего вида, то этот вид сам по себе исчезнет из-за вырождения).
Описанный в разделе алгоритмов распознавания образов метод группового учета аргументов так же относится к разряду эволюционных. Его можно представить как следующий цикл:
Как мы видим, налицо все признаки эволюционного алгоритма - отбор (селекция) и генерация нового поколения.
Генетический алгоритм является самым известным на данный момент представителем эволюционных алгоритмов, и по своей сути является алгоритмом для нахождения глобального экстремума многоэкстремальной функции. ГА представляет собой модель размножения живых организмов.
Для начала представим себе целевую функцию от многих переменных, у которой необходимо найти глобальных максимум или минимум:
f(x1, x2, x3, …, xN)
Для того чтобы заработал ГА, нам необходимо представить независимые переменные в виде хромосом. Как это делается?
Как создать хромосомы?
Первым Вашим шагом будет преобразование независимых переменных в хромосомы, которые будут содержать всю необходимую информацию о каждой создаваемой особи. Имеется два варианта кодирования параметров:
В случае если мы используем двоичное кодирование, мы используем N бит для каждого параметра, причем N может быть различным для каждого параметра. Если параметр может изменяться между минимальным значением MIN и максимальным MAX, используем следующие формулы для преобразования:
r = g*(MAX – MIN) / (2^N – 1) + MIN.
g = (r – MIN) / (MAX – MIN) * (2^N – 1)
где g – целочисленные двоичные гены,
r – эквивалент генов в формате с плавающей запятой.
Хромосомы в формате с плавающей запятой, создаются при помощи размещения закодированных параметров один за другим.
Если сравнивать эти два способа представления, то более хорошие результаты дает вариант представления в двоичном формате (особенно, при использовании кодов Грея). Правда, в этом случае мы вынуждены мириться с постоянным кодированием/декодированием параметров.
Как работает генетический алгоритм?
В общем, генетический алгоритм работает следующим образом. В первом поколении все хромосомы генерируются случайно. Определяется их "полезность". Начиная с этой точки, ГА может начинать генерировать новую популяцию. Обычно, размер популяции постоянен.
Репродукция состоит из четырех шагов:
и трех генетических операторов (порядок применения не важен)
Роль и значение селекции мы уже рассмотрели в обзоре эволюционных алгоритмов.
Кроссовер является наиболее важным генетическим оператором. Он генерирует новую хромосому, объединяя генетический материал двух родительских. Существует несколько вариантов кроссовера. Наиболее простым является одноточечный. В этом варианте просто берутся две хромосомы, и перерезаются в случайно выбранной точке. Результирующая хромосома получается из начала одной и конца другой родительских хромосом.
|
001100101110010|11000 |
--------> |
001100101110010 11100 |
|
110101101101000|11100 |
Мутация представляет собой случайное изменение хромосомы (обычно простым изменением состояния одного из битов на противоположное). Данный оператор позволяет более быстро находить ГА локальные экстремумы с одной стороны, и позволяет "перескочить" на другой локальный экстремум с другой.
|
00110010111001011000 |
--------> |
00110010111001111000 |
Инверсия инвертирует (изменяет) порядок бит в хромосоме путем циклической перестановки (случайное количество раз). Многие модификации ГА обходятся без данного генетического оператора.
|
00110010111001011000 |
--------> |
11000001100101110010 |
Очень важно понять, за счет чего ГА на несколько порядков превосходит по быстроте случайный поиск во многих задачах? Дело здесь видимо в том, что большинство систем имеют довольно независимые подсистемы. Вследствие этого, при обмене генетическим материалом часто может встретиться ситуация, когда от каждого из родителей берутся гены, соответствующие наиболее удачному варианту определенной подсистемы (остальные "уродцы" постепенно вымирают). Другими словами, ГА позволяет накапливать удачные решения для систем, состоящих из относительно независимых подсистем (большинство современных сложных технических систем, и все известные живые организмы). Соответственно можно предсказать и когда ГА скорее всего даст сбой (или, по крайней мере, не покажет особых преимуществ перед методом Монте-Карло) - системы, которые сложно разбить на подсистемы (узлы, модули), а так же в случае неудачного порядка расположения генов (рядом расположены параметры, относящиеся к различным подсистемам), при котором преимущества обмена генетическим материалом сводятся к нулю. Последнее замечание несколько ослабляется в системах с диплоидным (двойным) генетическим набором.
Эволюционное (генетическое) программирование
Данные, которые закодированы в генотипе, могут представлять собой команды какой-либо виртуальной машины. В таком случае мы говорим об эволюционном или генетическом программировании. В простейшем случае, мы можем ничего не менять в генетическом алгоритме. Однако в таком случае, длина получаемой последовательности действий (программы) получается не отличающейся от той (или тех), которую мы поместили как затравку. Современные алгоритмы генетического программирования распространяют ГА для систем с переменной длиной генотипа.
Каждый настоящий изобретатель, каждый творчески работающий конструктор ищут не просто новое, улучшенное ТР, а стремятся найти самое эффективное, самое рациональное, лучшее из лучших решений. И такие решения некоторым изобретателям удавалось находить. Это, например, конструкция книги, карандаша, гвоздя, брюк, велосипеда, трансформатора переменного тока, паровой машины и многих других ТО. Такие конструкции в первую очередь характеризуются тем, что они сотни или десятки лет массово производятся и используются без изменения, если не считать мелких усовершенствований.
Наивысшие достижения инженерного творчества заключаются в нахождении глобально оптимальных принципов действия и структур ТО.
Постановка задачи параметрической оптимизации. Прежде чем рассматривать постановку задачи поиска оптимального ТР для заданного физического принципа действия, разберем задачу более низкого уровня, которую называют задачей поиска оптимальных значений параметров для заданного ТР или сокращенно - задачей параметрической оптимизации. Эти задачи неизбежно приходится решать при поиске оптимального ТР, а кроме того, они имеют и самостоятельное значение.
Любое отдельное ТР, как правило, можно описать единым набором переменных (изменяемых параметров)
Х = (x1, ..., xn), (1)
которые могут изменять свои значения в некотором гиперпараллелепипеде
ai<=xi <=bi, i = l, ..., n, (2)
где для расширения области поиска не рекомендуется накладывать жестких ограничений на ai, bi.
Математическая модель проектируемого изделия ставит в соответствие каждому набору значений (1) некоторый критерий качества (функцию цели) f(х) и накладывает на переменные (1) дополнительные ограничения, представляемые чаще всего в виде системы нелинейных неравенств
gi (X) >= 0, j = 1,...,m, (3)
Тогда задача поиска оптимальных параметров ТР состоит в нахождении такого набора (1), который удовлетворяет неравенствам (2) и (3) и обеспечивает глобальный экстремум критерию качества. Для определенности будем считать, что отыскивается минимум, и, если обозначим через D область допустимых решений, удовлетворяющих неравенствам (2), (3), получим задачу математического программирования в n-мерном пространстве:
найти точку X*![]() D, такую, что
D, такую, что
![]() . (4)
. (4)
Часто в задачах параметрической оптимизации на переменные или часть из них наложены условия целочисленности или дискретности. В этом случае область поиска D становится заведомо многосвязной, а сама задача с математической точки зрения - многоэкстремальной.
Следует еще заметить, что задачи поиска оптимальных значений параметров в подавляющем большинстве случаев представляют собой многопараметрические многоэкстремальные задачи, в которых функциональные ограничения (3) "вырезают" замысловатые допустимые области. Объемы этих областей могут быть очень малыми по сравнению с объемами гиперпараллелепипедов (2). Однако, несмотря на такую сложность, большинство задач параметрической оптимизации можно вполне удовлетворительно решить существующими методами.
Постановка задачи структурной оптимизации. Среди задач поиска оптимальных ТР рассмотрим только подкласс, называемый задачами поиска оптимальных многоэлементных структур ТО или коротко - задач структурной оптимизации.
Строгое определение понятия структуры ТО дать затруднительно, поэтому укажем лишь некоторые инженерные и математические свойства, которые связаны с этим понятием.
С инженерной точки зрения разные структуры рассматриваемого класса ТО отличаются числом элементов, самими элементами, их компоновкой, характером соединения между элементами и т. д. Понятие структуры в большей мере аналогично понятию технического решения, данному в п. 3 гл. 1, однако имеются различия, которые вызывают необходимость введения этого дополнительного понятия. Во-первых, в рамках заданного физического принципа действия, как правило, существует более широкое множество ТР по сравнению с множеством, которое можно формально описать при постановке и решений задачи структурной оптимизации. Во-вторых, между отдельными ТР подразумеваются более существенные различия по конструктивным признакам, чем различия между отдельными структурами, иногда формально отличающимися значениями несущественных дискретных переменных. Например, на рис. 64 показаны две фермы моста с решеткой в виде равнобедренных треугольников, которые имеют одинаковые ТР, но разные структуры. Короче говоря, для заданного физического принципа Действия множества возможных ТР и множество возможных структур (для рассматриваемой задачи структурной оптимизации) пересекаются, но, как правило, не совпадают.
При этом одно ТР можно представить несколькими близкими структурами.
С математической точки зрения два варианта ТО будут иметь различную структуру, если соответствующие им задачи параметрической оптимизации по одному и тому же критерию качества и при условии выбора оптимальных параметров каждого элемента структуры имеют различные наборы переменных (1) и функции (3), т. е. для различных структур существуют различные задачи параметрической оптимизации. Под критерием качества также подразумевается физико-технический, экономический или другой показатель (масса, точность, мощность, стоимость и т. п.), по значению которого из любых двух структур можно выбрать лучшую.
 Постановку задач структурной оптимизации обычно начинают с
определения набора переменных по следующей методике.
Постановку задач структурной оптимизации обычно начинают с
определения набора переменных по следующей методике.
1. Задают такие переменные, чтобы они могли по возможности описать множество всех рациональных структур S0, которые в состоянии оценить существующая математическая модель в рассматриваемом классе ТО.
2. Просматривают и анализируют методы преобразования структур. Дополняют множество S0 подмножествами новых структур, которые можно синтезировать и оценить с помощью существующей или доработанной математической модели. В результате строится расширенное множество рассматриваемых структур S и описывающий его набор переменных, который обозначим вектором А. Пусть, например, задача структурной оптимизации допускает следующий набор А:
(k, L, i, j, ![]() , ...,
, ..., ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() ),
(5)
),
(5)
где k - число элементов в структуре;
L - число способов соединения элементов;
![]() - вектор,
описывающий геометрические, физические и другие свойства i-го
элемента;
- вектор,
описывающий геометрические, физические и другие свойства i-го
элемента;
i - номер элемента (1, ..., k),
![]() - вектор,
описывающий геометрические, физические и другие свойства j-го способа
соединения:
- вектор,
описывающий геометрические, физические и другие свойства j-го способа
соединения:
j - номер способа соединения (1,...,L);
![]() - вектор,
характеризующий положение i-го элемента в пространстве при j-м способе
соединения (i = 1, ..., k, j =l, ..., L);
- вектор,
характеризующий положение i-го элемента в пространстве при j-м способе
соединения (i = 1, ..., k, j =l, ..., L);
![]() - другие
переменные.
- другие
переменные.
3. Из вектора А выделяют вектор А' независимых переменных, которыми можно варьировать при поиске оптимальных структур. Для зависимых переменных задают алгоритм их определения через независимые переменные.
4. Вектор А' разделяют на вектор переменных A'S, обеспечивающих изменение структуры, и вектор переменных А'P, с помощью которых ставят и решают задачи параметрической оптимизации для заданной структуры. Вектор А'P состоит из набора общих переменных А'0, которые присутствуют при изменении любой структуры, и набора переменных А'C, изменяющихся при переходе от структуры к структуре. При решении задачи параметрической оптимизации для заданной структуры используется только определенная часть переменных из набора Ас.
Так, если в задаче структурной оптимизации с указанным набором переменных структура определяется способом соединения, то можно считать, что A'S есть одна переменная
j, А'C = {![]() , ...,
, ..., ![]() ,
, ![]() ), А'C =
{А'C1, …, A'CL),
), А'C =
{А'C1, …, A'CL),
где А'CJ, = {![]() ,
, ![]() , ...} - собственные переменные j-й структуры; штрих означает,
что среди соответствующих переменных выбраны независимые.
, ...} - собственные переменные j-й структуры; штрих означает,
что среди соответствующих переменных выбраны независимые.
Допустим, имеется алгоритм выбора из множества S подмножества всех допустимых структур {Si,..., Sm}, у которых существует хотя бы один набор значений параметров, удовлетворяющих заданным ограничениям. Допустим также, что для любой структуры SJ (j = 1, ..., m) можно решить задачу параметрической оптимизации, т. е. задать пространство переменных
, j = 1, …, m, (6)
и по единому критерию качества найти допустимые оптимальные параметры структуры SJ. Оптимальные значения параметров структуры SJ будем обозначать через X*J.
Тогда задаче структурной оптимизации можно дать следующую формулировку.
Имеется m nJ-мерных параллелепипедов
![]() , i = 1,
…, nJ, j = 1, …, m, (7)
, i = 1,
…, nJ, j = 1, …, m, (7)
как с непрерывным, так и с дискретным характером
изменения переменных ![]() . Для каждого из параллелепипедов задана по единому критерию
качества целевая функция
. Для каждого из параллелепипедов задана по единому критерию
качества целевая функция
![]() , j = 1,
…, m, (8)
, j = 1,
…, m, (8)
и система ограничений
![]() , r = 1,
…, pJ, j = 1, …, m, (9)
, r = 1,
…, pJ, j = 1, …, m, (9)
Требуется найти точку ![]() , принадлежащую j*-му
параллелепипеду, для которой
, принадлежащую j*-му
параллелепипеду, для которой
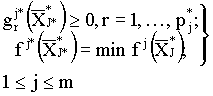
Таким образом, задача структурной оптимизации состоит в нахождении глобально-оптимальной структуры и глобально-оптимальных значений переменных внутри этой структуры, т. е. эту задачу можно назвать также задачей структурно-параметрической оптимизации.
К задачам структурной оптимизации относится задача выбора оптимальной компоновки ТО.
Отметим некоторые особенности задач структурной оптимизации. Во-первых, почти всегда в этих задачах одновременно присутствуют и дискретные, и непрерывные переменные, т. е. задачи структурной оптимизации в общем случае относятся к смешанным задачам математического программирования. Во-вторых, при структурных преобразованиях изменяются число и характер переменных и соответственно функции ограничений и целевые функции. Что касается характера многосвязной области поиска, то отдельные подобласти или имеют различную размерность или (при совпадении размерности) образованы различными наборами переменных.
Алгоритм поиска глобально-оптимального решения можно использовать для решения задач как параметрической, так и структурной оптимизации. Укрупненная блок-схема алгоритма включает четыре процедуры:
1) синтез допустимой структуры (СДС), обеспечивающий выбор допустимого решения из любой подобласти всей области поиска;
2) шаг локального поиска (ШЛП), обеспечивающий переход от одного решения к другому допустимому решению, как правило, той же структуры, но с улучшенным значением критерия; под шагом локального поиска можно понимать некоторый условный шаг по какому-либо алгоритму поиска локального экстремума (например, одна итерация по методу наискорейшего спуска);
3) глобальный поиск, управляющий работой процедур СДС и ШЛП;
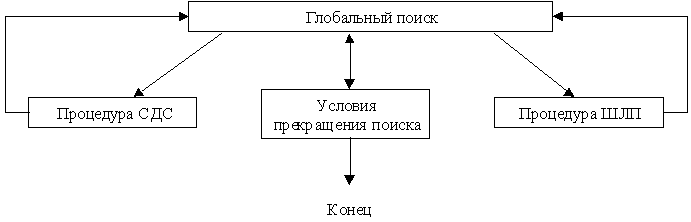
4) проверка условий прекращения поиска, определяющая конец решения задачи
Приведем основные рекомендации построения процедур СДС и ШЛП.
В некоторых случаях построение процедуры СДС можно свести к предварительному составлению набора допустимых структур, из которого выбирают структуры при каждом обращении к процедуре СДС. Если суть этой процедуры состоит в выборе по возможности допустимого набора переменных структурной оптимизации, то представляется полезным включать в нее правила выбора переменных, основанные на эвристических соображениях, аналитических и экспериментальных исследованиях, изучение опыта проектирования и эксплуатации аналогичных TО. Для некоторых сложных или малоизученных задач проектирования трудно построить процедуру СДС, обеспечивающую получение допустимых структур. В этом случае, в процедуру целесообразно включать операции преобразования недопустимых структур в допустимые. Набор таких операций можно составить из подходящих эвристических приемов (для задач, связанных с техническими объектами сборники таких приемов можно найти в соответствующей литературе, в которой решение изобретательских задач рассматривается более подробно). Преобразование недопустимых структур в допустимые можно также решать как задачу оптимизации. В диалоговом режиме работы санкцию процедуры СДС может взять на себя проектировщик.
В целом по процедуре СДС можно дать следующие рекомендации, направленные на повышение вероятности выбора допустимых структур и снижение объема вычислений по оценке недопустимых:
способы выбора значений переменных должны содержать правила, отсекающие заведомо нерациональные и недопустимые значения переменных и их комбинации;
ограничения следует проверять не после построения структуры в целом, а по возможности в процессе построения, что позволяет сократить лишнюю работу по ненужным построениям и в ряде случаев сразу внести поправки по устранению дефектов структуры;
проверяемые ограничения должны быть упорядочены по снижению вероятности их нарушения; такое упорядочение иногда можно проводить автоматически в процессы решения задачи.
Процедуры ШЛП включают обычно способы изменения переменных, ориентированные на решение задач как структурной, так и параметрической оптимизации. Приведенные рекомендации по построению процедур СДС можно использовать и при построении способов локального изменения дискретных переменных. Для изменения непрерывных переменных, как правило, применяют различные алгоритмы локального поиска. Ниже указаны наиболее предпочтительные (о ГА смотри замечание ниже).
В качестве процедуры глобального поиска используется алгоритм конкурирующих точек. В основе этого алгоритма лежит принцип эволюции популяции живых организмов, находящихся в ограниченном пространстве, например, на острове. В такой популяции резко обостряется конкуренция между отдельными особями. В связи с этим в основу алгоритма конкурирующих точек положены следующие положения:
поиск глобального экстремума осуществляется несколькими конкурирующими решениями (точками);
условия конкуренции одинаковых для всех решений;
в определенные моменты некоторые "худшие" решения бракуются (уничтожаются);
последовательный локальный спуск каждого решения (вначале грубый, затем более точный) происходит независимо от спуска других решений.
Конкуренция позволяет за счет отсева решений, спускающихся в локальные экстремумы, достаточно быстро находить глобальный экстремум в задачах, для которых значение функционала, осредненное по области притяжения глобального экстремума, меньше значения функционала, осредненного по всей области поиска, а область притяжения глобального экстремума не слишком мала.
Алгоритм конкурирующих точек - один из наиболее простых и эффективных по сравнению с другими распространенными алгоритмами поиска глобального экстремума. Так, например, трудоемкость поиска (затраты машинного времени) по этому алгоритму на порядок меньше по сравнению с алгоритмом случайного перебора локальных экстремумов и на два порядка меньше по сравнению с методом Монте-Карло.
Для удобства изложения алгоритма решение будем называть также точкой (в многомерном пространстве поиска) и независимо от того, решается ли задача параметрической оптимизации (1)-(4) или задача структурной оптимизации (6)-(9), будем обозначать его X.
Алгоритм конкурирующих точек в общем виде включает следующие операции.
1. По процедуре СДС синтезируется l (l = h + l0) точек
![]() (j = 1, ...,
l), в которых определяется значение минимизируемой функции
(критерия сравнения). Из этих l точек отбирается h точек, имеющих наилучшие значения критерия, которые в
дальнейшем называются основными. Запоминается наихудшее значение
критерия основных точек j0. При
этом считается, что совершен нулевой глобальный (групповой) шаг поиска
(t = 0).
(j = 1, ...,
l), в которых определяется значение минимизируемой функции
(критерия сравнения). Из этих l точек отбирается h точек, имеющих наилучшие значения критерия, которые в
дальнейшем называются основными. Запоминается наихудшее значение
критерия основных точек j0. При
этом считается, что совершен нулевой глобальный (групповой) шаг поиска
(t = 0).
Таким образом, на t-м групповом шаге поиска имеем основные точки
![]() , (10)
, (10)
и, соответственно, невозрастающую последовательность чисел
j 0, j1, …, j t. (11)
2. Каждая основная точка делает шаг локального поиска, в результате чего точки (10) переходят в новую последовательность
3. Синтезируется lt+1 дополнительных допустимых точек, каждой из которых разрешается сделать t+1 шагов локального поиска при условии, что после каждого шага с номером t (0 <= t <= t) ее критерий не хуже, чем соответствующий член последовательности (11). При нарушении этого условия точка исключается и не участвует в дальнейшем поиске глобального экстремума. Таким образом, имеется q (q <= l t+1) дополнительных точек, сделавших t + 1 шаг локального поиска:
4. Среди точек (12) и (13) отбирается h точек с лучшими критериями:
![]() , (14)
, (14)
которые являются основными на (t + 1)-м групповом шаге поиска. Значение худшего критерия точек из последовательности (14) дополняет последовательность (11) числом jt+1.
5. Цикл по пп. 2-4 повторяется до нахождения глобального экстремума по заданным условиям прекращения поиска. В качестве условий прекращения поиска могут быть использованы, например, выполнение заданного числа Т групповых шагов.
Считая параметры li независимыми от i, будем иметь только два настраиваемых параметра алгоритма; h - число основных точек и l - число дополнительных точек.
Проведенные исследования позволяют рекомендовать следующие оптимальные значения этих параметров: h = 2…3, l = 12…18. Для простоты реализации алгоритма можно брать постоянные значения h и l.
В качестве процедуры ШЛП рекомендуется использовать следующие алгоритмы поиска локального экстремума:
алгоритм случайного поиска в подпространствах;
алгоритм случайного поиска с выбором по наилучшей пробе;
алгоритм сопряженных градиентов;
алгоритм Нельдера-Мида.
Рекомендуемый алгоритм случайного поиска в подпространствах можно записать в виде следующих рекуррентных выражений:
![]() ;
;
![]() при
при ![]() .
.
Здесь h - число последовательно неудачных шагов поиска;
![]() определяется
по формуле:
определяется
по формуле:
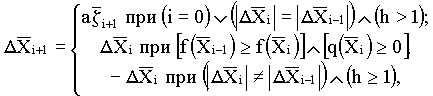
где a-максимальная величина рабочего шага поиска;
Вектор случайных чисел
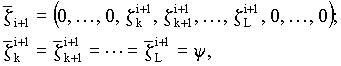
где y - случайное равномерно распределенное число, выбираемое из интервала [-1, 1]; k и L-случайные целые числа, распределенные на отрезке [1, n] и упорядоченные соотношением k <= L.
Имеются и другие модификации этого алгоритма, которые могут оказаться более эффективными.
Как можно заметить, ГА представляет собой смешанный алгоритм как для поиска глобального экстремума, так и для поиска локального. Это дает нам возможность упростить схему поиска глобально-оптимальных структур за счет использования в ней ГА как в качестве алгоритма СДС, так и в качестве алгоритма ШЛП. Какие плюсы и минусы данной схемы? Плюсы - простота реализации, универсальность. Минусы - по сравнению со специальными алгоритмами СДС, которые будут давать нам гораздо больше жизнеспособных экземпляров, очень уменьшится скорость работы алгоритма. Таким образом, ГА предпочтительно использовать в следующих случаях: простые случаи, в которых программирование специального метода будет продолжаться гораздо дольше, чем поиск решения даже медленным методом; сложный случай, когда мы даже не знаем, с какой стороны подойти к задаче.
Интересно также отметить общие стороны ГА и алгоритма случайного поиска в подпространствах. Оба эти алгоритма при поиске оптимума изменяют не все возможные переменные, а только часть их. Это, казалось бы мелкое усовершенствование, ведет к поразительным результатам - эти алгоритмы в среднем дают трудоемкость нахождения решения на порядок ниже, чем метод сопряженных градиентов и на два порядка ниже, чем метод случайного поиска по всему пространству переменных. Другими словами, эти алгоритмы используют одно из свойств нашего мира - независимость различных подсистем объектов.
Возвращаясь к основному вопросу данных лекций - интеллектуальным задачам, скажем, что данные алгоритмы ведут себя как опытные инженеры при поиске неисправностей (очень интеллектуальная по всем параметрам задача), и соблюдают заповедь - "никогда не трогать все сразу, только по очереди".
Фонд физико-технических эффектов
Поиск физических принципов действия (ФПД) технических объектов и технологий - один из самых высоких уровней инженерного творчества, позволяющий получать принципиально новые решения, включая и пионерные. Однако разработка ФПД - это и наиболее сложная задача инженерного творчества, поскольку человек вынужден варьировать и оценивать не только конструктивные признаки, обычно хорошо обозримые и логически увязанные друг с другом. Здесь приходится абстрагироваться на уровне физико-технических эффектов (ФТЭ), не всегда очевидных и достаточно глубоко познанных. В отличие от новых комбинаций конструктивных признаков мысленно представить и оценить новые комбинации ФТЭ значительно труднее.
Главная трудность состоит в том, что инженер обычно знает до 200, а достаточно свободно использует не более 100 ФТЭ, хотя в научно-технической литературе их описано более 3000. Кроме того, в связи с возрастающими темпами развития науки и техники, число ФТЭ постоянно увеличивается. Таким образом, в наше время у разработчиков новой техники существует очень большой и возрастающий дефицит информации, необходимой для решения задач поиска новых ФПД.
Излагаемые в настоящей главе методы автоматизированного поиска новых
ФПД позволяют, во-первых, в большой мере устранить указанный дефицит
информации по ФТЭ; во-вторых, значительно облегчить получение новых
работоспособных комбинаций ФТЭ, т. е. новых ФПД изделий и
технологий.
Таблица 1. Пример карты описания физико-технических эффектов (ФТЭ)
| Тепловое расширение твердых тел | 3-21 |
| Тепловое расширение | 3 |
|
|
|
|
Сущность и схема ФТЭ Тепловое расширение твердых тел связано с несимметричностью (ангармонизмом) тепловых колебаний атомов, благодаря чему межатомные расстояния с ростом температуры увеличиваются, что приводит к изменению линейных размеров тела
Диапазоны изменения Диапазоны температур T1 и Т2 должны принадлежать одной аллотропической модификации и быть меньше температуры плавления. |
Математическая модель ФТЭ e=a*dT где e=dL/L1 – относительное удлинение dT = T2-T1 – разница температур a – коэффициент линейного расширения (берется из таблицы)
Существование обратного ФТЭ Нет Применение ФТЭ в технике В приборостроении, электротехнической промышленности, энергетике; при конструировании установок, приборов и машин, работающих в переменных температурных условиях, а также использующих тепловое расширение тел. |
В основе этих методов лежит база данных, в которой каждый ФТЭ имеет трехуровневое описание. На первом уровне дается самое короткое качественное описание ФТЭ. Второй уровень - это стандартная карта описания ФТЭ размером в одну страницу, где дается наиболее важная и легко обозримая информация о ФТЭ и его использование в технике. В табл. 1 приведен пример карты описания эффекта теплового расширения, из которого понятно содержимое рубрик описания, а также видно, что первый уровень описания включается в карту описания.
Третий уровень описания совместно с информацией второго уровня дает более подробное описание ФТЭ, объем которого обычно составляет 5-10 машинописных страниц.
Существуют элементарные структуры ФПД, которые основываются на одном ФТЭ. Для поиска (синтеза) таких ФПД, определяют соответствие между физической операцией, которую требуется реализовать, и ФТЭ, с помощью которого можно осуществить такую реализацию.
Если принять во внимание формализованное описание физической операции и ФТЭ, можно отметить следующее соответствие компонент:
AT<-> A, CT<-> C,
где А и С - входные и, соответственно, выходные потоки вещества, энтропии и т.д.
Так, например, для физической операции АТ - "сила", СТ - "линейная деформация" будет найден ФТЭ: закон Гука (А - сила, напряжение; С - линейная деформация, В-упругое тело), на котором основаны пружинные весы.
В технике также распространен другой тип элементарной структуры ФПД, основанный на многократном или суммарном использовании одного и того же ФТЭ. Например, в катушках индуктивности каждый виток проводника реализует преобразование электрического тока в электромагнитное поле. Аналогичную структуру ФПД имеют аккумуляторные батареи, выпрямители, конденсаторы, усилители и т. д.
Однако большинство ФПД изделий имеют сложную структуру, в которой используется одновременно несколько различных ФТЭ. Синтез и работа таких ФПД основывается на следующем правиле совместимости ФТЭ.
Два последовательно расположенных ФТЭ
(Ai, Bi, Ci), (Ai+1, В i+1, C i+1)
будем считать совместимыми, если результат воздействия Сi предыдущего ФТЭ эквивалентен входному воздействию A i+1 последующего ФТЭ, т. е. если Ci и А i+1 характеризуются одними и теми же физическими величинами и имеют совпадающие значения этих величин.
Два совместимых ФТЭ могут быть объединены, при этом входное воздействие Ai, будет вызывать результат C i+1, т. е. получается преобразователь
Ai => Bi => (Ci <-> Ai+1)=> В i+1 => C i+1 (15)
В связи с этим дадим следующее определение ФПД.
Физическим принципом действия ТО будем называть структуру совместимых и объединенных ФТЭ, обеспечивающих преобразование заданного начального входного воздействия А1 в заданный конечный результат (выходной эффект) Сn. Здесь имеется в виду, что число используемых ФТЭ не менее n.
Уточним понятие совместимости ФТЭ. Для имеющегося фонда ФТЭ имеет место три вида совместимости:
качественная совместимость по совпадению наименований входов и выходов (пример совместимости: "электрический ток - электрический ток");
качественная совместимость по совпадению качественных характеристик входов и выходов (пример несовместимости: " электрический ток переменный - электрический ток постоянный");
количественная совместимость по совпадению значений физических величин (пример совместимости: " электрический ток постоянный I=10A, U=110В - электрический ток постоянный I = 5-20 A, U = 60-127 В").
Поиск допустимых ФПД. Опишем порядок работы с учебной системой автоматизированного синтеза ФПД. Работа по поиску допустимых ФПД состоит из четырех этапов.
1-й этап. Подготовка технического задания. При подготовке технического задания составляют описание функции разрабатываемого ТО и его физической операции. Описание физической операции рекомендуется делать с учетом синонимов в наименованиях "выходов" и "входов", т.е. в итоге может получиться несколько вариантов операции. Если имеется словарь технических функций, то эта работа выполняется значительно быстрее и правильнее.
После формулировки вариантов физической операции по компонентам АТ, СТ, с помощью словаря "входов" и "выходов" (табл. 2) описывают совпадающие или близкие по содержанию входы и выходы, т. е. выявляют соответствия
(АТ<->А1), (СТ<-> Сn).
Наличие таких соответствий позволяет сформулировать одно или несколько технических заданий
А1=> Сn. (16)
2-й этап. Синтез возможных ФПД. По техническому заданию (16) ЭВМ выбирает из фонда ФТЭ такие, у которых одновременно выполняются условия
(АJ<-> А1), (СJ<-> Сn).
Все эти ФТЭ представляют ФПД, использующие один ФТЭ.
Далее из фонда ФТЭ выбираются такие, которые обеспечивают выполнение условия
Ai<-> A1, i = 1,…., k (17)
или
CJ<-> Cn, j = 1, …, m. (18)
Из множеств ФТЭ (17) и (18) выбирают такие пары ФТЭ, у которых выполняется условие пересечения
Ci<-> AJ,
указывающее на то, что эти пары ФТЭ совместимы и образуют ФПД из двух ФТЭ по формуле (15)
Ai => Bi => (Ci <-> AJ) => ВJ => CJ. (19)
Для множеств ФТЭ, отобранных по условиям (17) и (18), при невыполнении условия (19) проверяется возможность образования цепочек из трех ФТЭ:
Ai => Bi => (Ci <-> At) => Вt => (Ct <-> AJ)=> ВJ => CJ,
где i = 1,…., k, j = 1, …, m, t = 1, …, km..
Таблица 2. Фрагмент словаря "входов" ("выходов")
|
╧ п/п |
Наименование "входа" ("выхода") |
Качественная характеристика "входа" ("выхода") |
Физическая величина, характеризующая "вход" ("выход") |
|
|
Наименование |
Обозначение |
|||
|
1 |
Электрическое поле |
Постоянное Переменное Однородное Неоднородное Высокочастотное |
Напряженность электрического поля. Разность потенциалов ЭДС |
D j e |
|
2 |
Магнитное поле |
Постоянное Переменное Однородное Неоднородное |
Магнитная индукция Магнитный поток |
В Ф |
|
3 |
Электромагнитное поле |
Ультрафиолетовое Видимое Инфракрасное Рентгеновское Линейно поляризованное Эллиптически поляризованное |
Интенсивность Частота Длина волны Амплитуда |
S n l A |
|
4 |
Акустическая волна |
Звуковая Ультразвуковая |
Частота Мощность излучения Интенсивность |
f P J |
|
5 |
Сила |
- |
Сила |
F |
|
6 |
Температура |
- |
Температура |
T |
Далее для тех же множеств проверяется возможность образования цепочек из четырех и из пяти ФТЭ.
Встречным наращиванием цепочек совместимых ФТЭ от A1 до Сn можно получать новые варианты ФПД, включающие и большее число ФТЭ. Однако при числе ФТЭ, превышающем пять, резко возрастает вычислительная сложность такого метода из-за комбинаторного характера задачи и существенного роста числа анализируемых промежуточных вариантов. Кроме того, ФПД с числом ФТЭ более пяти с практической точки зрения обычно не относятся к наиболее рациональным.
Изложенный алгоритм представляет собой один из возможных простых способов синтеза ФПД. Можно использовать и другие алгоритмы, ориентированные на предварительно организованную базу данных по ФТЭ.
Суть этой организации состоит в определенном построении сетевых графов из всех совместимых ФТЭ.
Система синтеза ФПД по введенному техническому заданию позволяет получать варианты ФПД. Кроме того, в ней в качестве дополнительных исходных данных могут быть использованы следующие ограничения:
максимальное число ФТЭ в цепочке (например, n < 4);
число получаемых вариантов ФПД (например, m < 20);
запрещение (или предпочтительность) использования определенных входов А и выходов С;
запрещение (иди предпочтительность) использования определенных объектов В;
другие ограничения.
3-й этап. Анализ совместимости ФТЭ в цепочках. Полученные на 2-м этапе цепочки возможных ФПД удовлетворяют только .качественной совместимости по совпадению наименований входов и выходов. Хотя среди полученных ФПД ЭВМ может отсекать варианты по условию совместимости качественных характеристик, а в промышленной системе - по количественной совместимости, иногда бывает целесообразно данную работу выполнять в полуавтоматическом режиме
4-й этап. Разработка принципиальной схемы.
В данной главе рассмотрены некоторые алгоритмы, которые мы можем отнести к эволюционным и/или переборным. Сразу обращает на себя внимание тот факт, что во всех эволюционных алгоритмах в той или иной мере присутствует перебор, который придает им одно уникальное свойство - универсальность. В то же время, ни один из передовых алгоритмов не использует перебор в чистом виде. Все они имеют те или иные схемы для предотвращения полного перебора, для чего практически всегда используется такое свойство окружающего нас мира (не только материального), как ступенчатость - ограниченность воздействия одних систем на соседние, в результате чего появляется возможность организовывать параллельный поиск.
Автор данного конспекта лекций является сторонником мнения, что мир, в котором мы живем, является миром со слабыми причинно-следственными связями. Что имеется в виду?
Представим себе, что Вы пишете статью, а за окном упал осенний кленовый лист, которого Вы не видите. Если такое событие повлияет на текст, который вы пишете, то можно сказать, что наш мир настолько насыщен причинно-следственными связями, что любое событие окажет большое или малое влияние на события, произошедшие после него. Такой мир будем называть сильносвязанным.
Однако весь наш опыт доказывает обратное. К примеру, на самолет не успел один из пассажиров. На подавляющее большинство остальных пассажиров это не окажет никакого влияния. Дело в том, что обычно реальные системы имеют так называемые "ступенчатые функции", которые при небольших вариациях возмущающих воздействий не дают им распространяться к другим системам. Более того, именно благодаря слабой связанности мира мы можем выделить в нем отдельные системы, а в них подсистемы. В противном случае весь мир представлял бы собой одну настолько сложную систему, что самый великий гений не мог бы разобраться и жить в этом безумном мире, не говоря уж об обычной амебе.
Биологическим системам управления приходится адаптироваться к окружающей среде, принимая форму зеркального отражения ее структуры, поэтому в нашем мозгу всегда можно выделить подсистемы, которые никоим образом не должны влиять друг на друга в обученном состоянии. К примеру, рассмотрим человека, управляющего автомобилем с ручной коробкой передач. В тот момент, когда его правая рука переключает очередную передачу, левая должна продолжать удерживать руль в положении "прямо" независимо от того, что делает правая. Если данные подсистемы будут объединены, то при каждом переключении передачи автомобиль начнет вилять, что и случается у новичков. В процессе обучения вождению автомобиля происходит ослабление внутренних связей между нейронными ансамблями, управляющими процессами переключения передач и вращения руля, в результате чего устраняется эффект "виляния". Можно привести и более простой пример: человек с нормальной координацией движений, продолжает двигаться прямо вне зависимости от того, куда повернута его голова.
Таких примеров можно привести множество.
Рассмотрим теперь построение алгоритмов оптимизации структуры и параметров. Несмотря на их огромное разнообразие, можно выделить основную черту: оптимизируемый объект является "черным ящиком", который оптимизируется целиком. Для полученного на очередном шаге набора параметров достигнутый результат оценивается только по общей оценочной функции. Это приводит к тому, что малые улучшения в работе отдельных локальных подсистем не закрепляются на фоне ухудшения работы остальных. Можно назвать еще некоторые недостатки подобной реализации - сложности в подборе шага, коэффициента мутаций и т. д., но это уже решаемые мелочи.
Незакрепление малых улучшений в подсистемах при последовательной адаптации приводит к одному результату - в сложных системах, состоящих из большого количества подсистем, скорость обучения катастрофически снижается.
Здесь примером могли бы служить N колес с буквами А и В на ободе, где буквы А занимали бы k-ю долю окружности, а В - остальную ее часть. Все колеса приводят во вращение и дают им остановиться; остановка колеса на букве А считается "успехом". Сравним три способа сложения этих частных успехов в Большой Успех, который будем считать достигнутым только тогда, когда все колеса остановятся на букве А.
Случай 1. Приводятся во вращение все N колес; если все они дадут букву А, регистрируется Успех и пробы заканчиваются; в других случаях колеса снова приводятся во вращение - и так далее, пока все А не появятся сразу. В этом случае потребуется в среднем (1/k)*N проб.
Случай 2. Вращается 1-е колесо; если оно остановится на А, оно остается в этом положении; в противном случае его вращают снова. Когда оно, наконец, остановится на А, таким же образом вращают 2-е колесо и т. д. Так поступают до тех пор, пока все N колес не остановятся на секторе А. Здесь в среднем потребуется N/k проб.
Случай 3. Приводятся во вращение все N колес; те, которые покажут А, остаются в этом положении, а те, которые покажут В, вращаются снова. При дальнейших появлениях А соответствующие колеса также остаются в покое. Среднее число проб равно среднему числу проб в самой длинной серии из N серий проб с одним колесом и может быть найдено из распределения длин таких серий; оно будет несколько больше 1/k.
Случайный поиск служит полным аналогом 1-го случая. Многие из остальных алгоритмы занимают промежуточное положение между первым и вторым случаем (случайный поиск в подпространствах, генетический алгоритм и т. д.). Очевидно, что человек как правило решает свои проблемы независимо друг от друга, что соответствует третьему случаю.
Таким образом, перспективные алгоритмы должны предусматривать возможность разделения целей на подцели, которые не зависят друг от друга.