"Разработка и исследование компьютеризированной системы процесса обучения и контроля знаний персонала Запорожской атомной электростанции"

e-mail автора: lebedenko@ukrtop.com

1 Общая характеристика работы

Целью данной магистерской работы является создание и исследование компьютеризированной системы процесса обучения и контроля знаний персонала Запорожской атомной электростанции, которая позволит усовершенствовать процесс обучения и контроля знаний путём переноса учебного курса на компьютер. За счёт чего исключаются ошибки человеческого фактора в контроле знаний. Что также позволит корректировать курс обучения в соответствии с особенностями восприятия материала обучаемым.

В соответствии с поставленной целью, основными задачами являются:

• анализ существующих систем и методов процесса обучения и контроля знаний;
• разработка матетматического обеспечения компьютеризированной системы;
• разработка программного обеспечения;

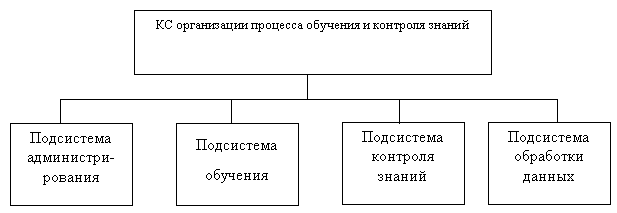
Структура данной системы представлена на рисунке.

Рис. 1 Структура КС организации процесса обучения и контроля знаний

Подсистема администрирования решает следующие задачи:

• настройка системы, т.е. указание путей хранения баз данных;
• назначение прав доступа;
• регистрация обучаемого.

Подсистема обучения решает следующие задачи:

• представление данных по выбранному вопросу;
• оценка усвоения материала.

Подсистема контроля знаний решает следующие задачи:

• назначение курса проверки знаний;
• тестирование;
• подсчёт затраченного времени;
• фиксирование ответов.

Подсистема обработки данных решает следующие задачи:

• анализ знаний тестируемого;
• вывод статистических данных (данные по группам, по специальностям, по должностям и пр.);
• оценка уровня забываемости и восстановления знаний;
• расчёт стратегии обучения.

Актуальность работы обусловленна:

1. Необходимостью постоянного повышения эффективности процесса обучения и контроля знаний, а также необходимостью разработки и апробации методов и средств, которые разрешают существенным образом улучшить подготовку специалистов.
2. Необходимостью усовершенствования системы профессионального отбора и подготовки специалистов (оперативного персонала АЭС) в связи с повышением требований к квалификации.
3. Необходимостью усовершенствования информационно - методического обеспечения компьютерной технологии обучения.

Научная новизна основных положений работы состоит в следующем: положения, рассмотренные в работе являются развитием одного из направлений в теории обучения, а именно математического моделирования процесса обучения. Предложенный в диссертационной работе подход к математическому моделированию процесса обучения и реализация таких моделей расширяют возможности при исследовании процессов получения, забывания и восстановления знаний обучаемыми, а также возможности при разработке методологической основы применения информационных технологий в процессе образования и обучения.

Практическая ценность работы состоит в следующем: обоснована целесообразность использования моделей статистической теории обучения и контроля знаний, а также моделей теории стохастических процессов при обучении оперативного персонала АЭС; впервые при подготовке оперативного персонала АЭС реализованы модели статистической теории обучения и контроля знаний (результаты исследований были использованы при разработке автоматизированных систем обучения и контроля знаний оперативного персонала Запорожской АЭС).

Математические модели, алгоритмы и программное обеспечение, которые предложенны в работе, введены в Учебно-тренировочном центре Запорожской АЭС (акт о внедрении).

2 Содержание работы

В первой главе излагается подробное описание объекта компьютеризации. Предлагается его структура с описание всех составных подсистем и задач. Также представляются потоки информации на информационной схеме объекта с подробным описанием каждого элемента схемы. Произведён анализ входной и выходной информации. Установлены связи между потоками информации, а также связывающие их критерии и величины. В первой главе также предоставляется анализ существующих автоматизированных систем обучения. Выявлены достоинства и недостатки каждой системы.

Вторая глава посвящена математическому моделированию процесса обучения и контроля знаний. В ней представлен обзор существующих моделей и методов программного обучения, также рассмотрена проблема понятий и определений обучения и контроля знаний. Рассмотрен вопрос статистической теории обучения и контроля знаний, включающий модели восстановления знаний.

В третьей главе изложены проблемы разработки компьютеризированной системы обучения и контоля знаний такие как: технические средства реализации, включая конфигурацию локальной сети и отдельных компьютеров. Рассмотрены вопросы применеия выбранной математической модели в заданных условиях.

Результатом использования данной компьютеризированной системы должно стать сокращение времени обучения и увеличение объема воспринимаемой информации, а также более точный и быстрый контроль. Данная система предназначена для сетевого использования, что значительно упрощает доступ к информации и сокращает время обучения и контроля при больших группах обучаемых.

Понятия и определения процесса обучения и контроля знаний

В современном обществе роль информационных технологий чрезвычайно важна, они занимают сегодня центральное место в процессе интеллектуализации общества, развития его системы образования и культуры. Система образования и наука есть одним из объектов процесса информатизации общества. В сфере образования при применении информационных технологий необходима реализация таких задач:

• поддержка и развитие системности мышления обучаемых;
• поддержка всех видов познавательной деятельности человека в приобретении знаний, развитие и закрепление навыков и умений;
• реализация принципа индивидуализации учебного процесса при сохранении его целостности.

Поэтому недостаточно овладеть той или иной информационной технологией. Необходимо выделить и наиболее эффективно использовать те ее особенности и возможности, которые могут в какой-то мере обеспечить решение указанных выше задач.

В конечном счете все достижения в области применения информационных технологий в сфере образования, создание и сопровождение банков данных и баз знаний, экспертных систем и других видов информационных технологий должны служить одной цели - разработке методологической основы применения информационных технологий в процессе образования и обучения. Необходимо научиться правильно, оптимально и безопасно применять компьютер в всей системе образования в целом.

Обучение определяется как процесс управления внешней и внутренней активностью обучаемого, в результате которой у него формируются определенные знания, навыки и умения.

Возможности человека определяются через знание, навыки и умения, необходимые для эффективного выполнения задач. Эти категории можно определить следующим способом.

Знание - упорядоченная совокупность сведений, обычно фактического или процедурного характера, использование позволяет адекватное выполнение работы. Владение знаниями не говорит о том, что они будут использованы.

Навык - это способность легко и точно выполнять действия, необходимые во время работы. Говоря про навык, необходимо указывать некоторый нормативный уровень, достижение которого нужно для эффективного выполнения работы.

Умение обычно понимается как способности, необходимые для выполнения какой-то функции в работе. Очень часто для проявления умения необходимо использование каких-нибудь основных знаний.

Довольно долго технология обучения и контроля знаний отождествлялась с простым использованием технических средств обучения и контроля. Она рассматривался лишь как способ технологизации (автоматизации) процесса обучения и контроля.

Со временем технологию обучения и контроля знаний стали использовать для обеспечения научными принципами процесса проектирования новой или модернизованной практики обучения. Однако, это требует научного обоснования целей и задач обучения и контроля, тщательный отбор адекватного предметного содержания, выбор объектов изучения и видов деятельности для разработки учебного курса.

Моделирование обучения является одним из направлений при исследовании проблем искусственного интеллекта. В данной работе рассматриваются вопросы, связанные с процессом обучения и контролем знаний оперативного персонала АЭС, поэтому естественным будет рассмотрение работ этого направления.

Современный уровень развития компьютерной техники для подготовки операторов АЭС, с одной стороны, и накопленный опыт относительно использования элементов контроля и оценки полученных знаний с другой, является базой для создания и использования компьютерных автоматизированных систем обучения и контроля знаний.

Характер самого процесса обучения и контроля знаний, его технология должны измениться. Это обусловлено тем, что эффективность традиционного подхода в современных условиях, когда новые знания появляются и устаревают намного быстрее, чем время их "освоения", нельзя считать приемлемой. Подводя итоги анализа основных направлений, можно сказать, что проблеме обучения и контроля знаний в данное время отводится большое внимание. Вместе с тем, на данный момент сформировалась целая серия теоретических и прикладных проблем, которые обуславливают необходимость проведения дальнейших исследований.

Анализ математических моделей обучения и контроля знаний

После ранних работ Г.Эббингауза и Э.Торндайка эмпирические данные, полученные при обучении, стали выражать в виде уравнений, которые не опирались на какую-то теорию, а лишь интерпретировали имеющиеся данные [1, 2]. Математика здесь, прежде всего, была применена для описания эмпирических функций. Например, Эббингауз предположил, что частица материала, который забывается с течением времени, возрастает как логарифм времени, которое протекло с момента начала обучения. Наиболее распространенным методом описания результатов эксперимента обучения возникла "кривая обучения", то есть график, который изображает, как в условиях заданного эксперимента от пробы к пробе изменяются характеристики обучаемого или группы обучаемых. В качестве "функции обучения" предлагались разнообразнейший аналитические функции, в том числе гипербола, функция экспоненциального роста, арктангенс. Однако ни одна из этих функций не была получена на основе фундаментальной теории обучения.

О.Щукаревым было выведено следующее уравнение:

,

где - усвоение, обусловленное числом правильных воспроизведений (успехов) за единицу времени;

- число испытаний за единицу времени;

а - граница усвоения при п ® ∞; b и с - константы.

Т.Робертсоном было предложенно уравнение вида:

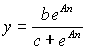
где у - усвоения; п - число испытаний за единицу времени; А = аb, а, с -константы (параметры обучаемого); b - граница усвоения при n ? ∞.

Л.Терстоун предложил следующую формулу (так называемый гиперболический закон обучения):

,

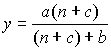где у - усвоения; п - число испытаний; а и с - константы; b -скорость обучения.

Дальнейшее развитие применения математических методов к исследованию проблем обучения связано с работами К.Халла [1, 2]. Он ввел переменную, которую назвал "силой навыка". Она выражается формулой

,

где - "сила навыка", или ассоциативная переменная, которая связывает стимул и реакцию; М - асимптотичное значение "силы навыка"; b - параметр, который выражает скорость обучения; п - число учебных попыток за единицу времени.

В 40 - 50-е года 20-го столетия в психологии начало складываться представление об обучении как о стохастическом процессе. Г.Бушем и Ф.Мостеллером [3], были сформулированы так называемые стохастические модели обученности. Для теории обучения особенно важным было сосредоточение внимания на вероятностях событий, последовательных эффектах и представлении данных в виде цепей Маркова.

В.Эстес, К.Берк, Дж.Миллер и прочие [1] разрабатывали подобные стохастические модели, которые получили название "линейные модели обучения". При построении этих моделей вводится вероятность р_n того, что обучаемый, в п-ом испытании даст ответ Е. Альтернативой будет ответ Ē. Соответственно, вероятность того, что обучаемый в п-ом испытании даст ответ Ē равняется 1 - р_n. В каждом испытании обучаемый даст ответ, получая при этом подкрепление, например, угадывает правильный ответ. В зависимости от подкрепляющего события E_j в п-ом испытании изменяется вероятность ответа в п+1-ом испытании:

,

где а_j и b_j. увеличивают или уменьшают вероятность ответа. Эти параметры зависят от того, подкрепляет ли событие Е_j ответ Е или Ē. Так в модели Буша-Мостеллера для случая двух альтернатив вводятся операторы

где - постоянные точки, то есть если , то p_п+1 = p_п (значение вероятности не изменяется).

В работе [2] описанные выше модели Халла и Терстоуна интерпретируются в терминах стохастических моделей. Так, модель Халла приобретает вид:

,

где р_n - вероятность приобретения навыка (или правильного ответа) в п-ом испытании; - константа.

В модели Терстоуна величина у интерпретируется как вероятность приобретения навыка р_n: у = 0 при п = 1 и у -> 1 при п ® ¥ . Уравнение Терстоуна приобретает вид:

где b - скорость обучения.

В модели Рестла вероятность изменяется по следующему правилу:

,

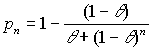где q - константа.

Кричевский выдвинул гипотезу о том, что после начального периода обучения возникает "внезапная" обученность, которая лежит в основе так называемой теории "прыжков". Вводится случайная величина х_n:

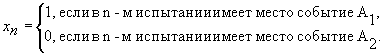
Тогда р_n =Р{х_n =1} - вероятность события А₁, q_n = Р{х_n = 0} = 1-p_n. Предположим, что обучаемый в начале попытки находился в некотором состоянии S₁, а потом после некоторого испытания п_i он переходит в состояние S₂ и остается в нем до конца эксперимента. В этом случае вероятность р_n имеет вид

Кроме того, вводится вероятность перехода из состояния S₁, в состояние S₂ на п-ом испытании:

где b - некоторый параметр, 0 < b < 1.

Дальнейшее развитие подобные модели получили в роботах Р.Аткинсона, Г.Бауера, Э.Кротерса [1].

Несмотря на то, что к настоящему времени разработанно большое количество разных подходов к моделированию процесса обучения, существует необходимость использования новых математических моделей и методов. К ним относятся методы статистической теории обучения и контроля знаний, методы теории стохастических процессов, которые можно использовать при обработке результатов контроля, при планировании обучения, при прогнозировании обучения, а также эти методы можно положить в основу создания современных автоматизированных систем обучения и контроля знаний. Разработке математических моделей обучения, основанных на положениях теории стохастических процессов, а также информационных технологий, которые применяют методы статистической теории обучения (в том числе при обработке результатов контроля знаний оперативного персонала АЭС), посвящена данная работа.

Элементы статистической теории обучения и контроля знаний

Наиболее известны в этой области работы О.П.Свиридова [4-6].

Используя методы статистической теории обучения и контроля знаний можно установить связь между потоком учебного материала, его усвоением и забыванием.

Пусть в момент времени t=0 информация воспринята обучаемым, а при t>0 ему задаётся вопрос по этому материалу. Если в момент t = t обучаемый даёт неправильный ответ на этот вопрос, то t отвечает времени забывания. Предполагается, что время t - непрерывная случайная величина с функцией распределения

.

В случае экспоненциального распределения

,

где λ - интенсивность забывания. Среднее время забывания равняется 1/λ. Вероятность правильного ответа на вопрос в интервале (0, t) .

Интенсивность забывания λ(t) имеет следующее значение. Величина λ(t)Δt представляет собой вероятность того, что обучаемый и что знает учебный материал по какому-то вопросу в интервале времени (0,t) забудет его в интервале времени (t, t + Δt).

В случае маленьких Δt получаем:

Для описания процесса забывания, кроме экспоненциального распределения используются также:

- распределение Вейбулла

.

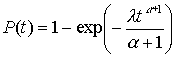Экспоненциальное распределение является частным случаем закона Вейбулла (при α = 0).

- распределение Эрланга

,

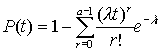где а - положительное целое число.

Экспоненциальное распределение является частным случаем распределения Эрланга при а=1.

Зная изменения во времени вероятности правильного ответа , можно определить математическое ожидание времени забывание вопросов определенного типа тем или иным обучаемым:

,

где .

Аналогично определяется дисперсия времени забывания:

.

В случае экспоненциального распределения получим следующие выражения для математического ожидания, дисперсии времени забывания и интенсивности забывания:

.

Рассмотрим модели восстановления знаний.

1. Мгновенное восстановление знаний, когда временем изучения или повторения учебного материала можно пренебречь по сравнению со временем забывания.

Пусть после изучения i-го вопроса в момент времени t=0 обучаемый дает на него правильный ответ. Но через время τ₁ он его забывает. В этот момент мгновенно происходит восстановление знаний обучаемого. Однако через некоторое время τ₂ обучаемый снова забывает вопрос. Этот процесс может продолжаться многократно. Момент времени п-го забывания вопроса равняется:

.

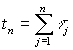Если восстановление знаний по забытому вопросу происходит мгновенно, то моменты забывания или восстановления знаний t₁, t₂, ..., t_n образовывают поток П_1i учебного материала по i-му вопросу.

В общем случае интервалы времени τ_j, j == 1,2,... являются случайными величинами, поэтому соответствующий поток также является случайным. Случайные величины τ_j, j =1,2,... в общем случае можно охарактеризовать функцией распределения в виде

.

Поток учебного материала с функцией распределения

называется простейшим или стационарным пуассоновским потоком.

2. Восстановление знаний с конечным временем восстановления, когда восстановление знаний сопоставимо со временем забывания.

Процесс забывания и восстановления с конечным временем восстановления знаний по ?-му вопросу можно представить в виде чередующихся интервалов забывания или сохранение (состояние Е₀ ) и восстановление знаний (состояние Е₁). В момент времени , соответственно учебной программе, начинается изучение учебного материала по какому-либо вопросу. Для этого требуется время φ_1. Потом начинается забывание данного вопроса. Продолжительность этого промежутка времени равняется τ_1. Для повторного восстановления знаний по данному вопросу обучаемому требуется время φ_2. Моменты времени

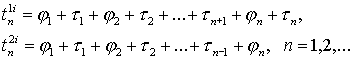
называются соответственно моментами забывания и восстановления знаний. Время восстановления забытого учебного материала меньше времени начального изучения, но эта разность небольшая.

Если функция распределения времени восстановления знаний равняется

,

то восстановление знаний называют экспоненциальным. При этом математическое ожидание и дисперсия времени восстановления знаний определяются формулами:

.

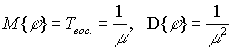Особенность экспоненциального восстановления знаний состоит в том, что если в момент времени t обучаемый занят восстановлением знаний, то распределение оставшегося времени восстановления будет экспоненциальным с тем же параметром m .

В качестве примера использования экспоненциального распределения времени восстановления знаний можно рассмотреть, вариант процесса обучения, когда обучаемому дается сначала информационно-справочный материал, а потом предлагается несколько упражнений с соответствующими объяснениями. При такой организации обучения вероятность усвоения положения или навыка повышается с ростом числа упражнений.

В статистической теории обучения рассматриваются стандартизированные методы контроля знаний, сущность которых состоит в том, что обучаемому предлагается выборка специальных задач и по ответам на нее делается суждение о его знаниях, умственном развитии или способностях [4, 5, 7, 8]. Стандартизированные методы имеют следующие положительные свойства: сокращение времени контроля; стандартизированность проведения проверки и анализа результатов; возможность представления результатов проверки в числовой форме; возможность математической обработки результатов проверки. К недостаткам стандартизированного контроля знаний можно отнести следующие: стандартизированные методы не всегда учитывают индивидуальные особенности обучаемых; при использовании стандартизированных методов принимается во внимание конечный результат решения задачи и не учитывается способ решения.

Пусть по какому-то курсу составлена контрольная программа из N вопросов. При подготовке вопросов должны учитываться цели обучения. Для любого обучаемого все вопросы программы делятся на две группы: вопрос, учебный материал которого усвоен (1); вопрос, учебный материал которого не усвоен (0).

Если число неправильных ответов по всей программе контроля составляет М, то их доля равняется

P = M / N.

Обычно число N довольно велико, поэтому целесообразно задавать не все N вопросов, а лишь выборку объема n. Пусть т - доля неправильных ответов на вопрос выборки, тогда оценка доли ошибок равняется

В этом случае для определения вероятности того, что при предложении п вопросов из N будет зафиксировано т ошибок по условию их общего числа М, можно использовать классическую формулу отношения числа благоприятных исходов к общему числу результатов.

Вопросы как генеральной совокупности, так и выборки из нее должны служить для проверки запоминания, понимания, степени обобщения, прочности усвоенных знаний, меры их автоматизации и т.д. Выборка вопросов должна быть представительной, чтобы по ее свойствам можно было бы судить о свойствах генеральной совокупности вопросов.

Если измерять правильность каждого ответа числом, то при предоставлении обучаемому п вопросов выборки, получим п чисел z₁,z₂,...,z_n. Наиболее часто используются два значения правильности - 0 и 1. При этом для правильного ответа z = 1, а для неправильного - 0. Иногда ответы оцениваются с использованием k-значимой шкалы. Истинность ответа при этом является дискретной величиной, которая принимает значение , причем z^(k) и z⁽¹⁾ отвечают максимальному и минимальному числу баллов.

Если N >> 1, п < 0.?N и Р = М / N = соnst, то предельным распределением есть биномиальное распределение

.

При пР = а и Р < 0.1 предельным распределением является распределение Пуассона

.

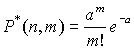Зависимость вероятности правильного решения вопроса от уровня знаний называют характеристической кривой. Уровень знаний может быть измерен, например, долей правильных решений вопросов выборки.

Определим через и P_ia, и=1,2,...,п вероятности правильного и неправильного ответа на вопрос и=1,2,...,п обучаемым со степенью подготовленности а. Вероятность Р^*(п,т) того, что обучаемый при ответе на п вопросов выборки допустит т ошибок можно определить по формуле обобщенного биномиального распределения

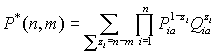
где z_i. равняется 1 или 0 соответственно при правильном или неправильном ответе. Как допустимую аппроксимацию вместо вышеприведенной формулы целесообразно использовать биномиальное распределение

со средней вероятностью

.

Эти соотношения применяются при отсутствии связи между вопросами. При наличии таких связей вероятность Р^*(п,т) может быть определена на основе использования цепей Маркова.

Обобщением при оценке ответов с использованием k-значимой шкалы является распределение вида:

,

где m_i, и = 1,2,:,k-число ответов истинности z^(и) на выборку с n вопросов;

P_i - доля вопросов со степенью усвоения z^(и) среди всех вопросов программы контроля.

Таким образом, приведенные выше соотношения являются основными соотношениями стандартизированного контроля знаний, когда оценка ставится по числу правильно или неправильно выполненных задач.

Список использованных источников

1. Аткинсон Р., Бауэр Г., Кротерс З. Введение в математическую теорию обучения: Пер. с англ. - М.: Мир, 1969. - 486 с.
2. Растригин Л.А., Зренштейн М.Х. Адаптивное обучение с моделью обучаемого. -Рига: Зинатне, 1988. - 160 с.
3. Буш Р., Мостеллер Ф. Стохастические модели обучаемости. - Г.: Физматгиз, 1962. - 484 с.
4. Свиридов А.П. Условные и безусловные алгоритмы диагностического контроля подготовки операторов ЭВМ. - М.: Моск. энерг. ин-т, 1987. -69с.
5. Свиридов А.П. Применение методов планирования эксперимента при обучении обучающих и контролирующих машин. - М.: Моск. энерг. ин-т, 1975.-65с.
6. Свиридов А.П. Основы статистической теории обучения и контроля знаний. - М.: Высшая школа, 1981. - 262 с.
7. Ржецкий Н.Н. Проверяющий стандартизированный контроль знаний и его зффективность. - К.: КИСИ, 1965. - 68 с.
8. Ржецкий Н.Н., Фиалко Э.И. Программированное обучение и стандартизированными контроль знаемый. - К.: Изд-во КГУ, 1969. - 108 с.
9. Стивенс С. Математика, измерение и психофизика. - В кн. Экспериментальная психология. Г., 1960. С.
10. Ю.Беспалько В.П. Основы теории педагогических систем. - Воронеж: Изд-во Воронеж.ун-та, 1977. - 304 с.
11. Лернер И.Я. Качества знаний учащихся. Какими они должны быть? -Г.: Знание, 1978. С
12. Чачко А.Г. Подготовка операторов энергоблоков. Алгоритмический подход. - Г.: Энергоатомиздат, 1986. - 230 с.

Главная