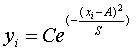(S>0) на интервале (0,1). Создать нейронную сеть такую, что при вводе этих значений на вход сети на выходе получали бы значения параметров С,A и S. | Назад | Семинар "Обзор возможностей системы MATLAB" 26.02.02 |
Neural Network Toolbox (v.4.0) MATLAB (v.6.0, v.6.1) - пакет программ, ориентированный на решение широкого спектра задач с использованием нейронно-сетевых алгоритмов. В пакете предусмотрена реализация практически всех типов нейронных сетей, описанных в литературе (15 разновидностей), а также предусмотрена возможность создания пользовательских сетей практически любой конфигурации. Нейронная сеть представлена в пакете как объект, включающий подобъекты и свойства, к большинству из которых имеется доступ из командного окна, что позволяет контролировать поведение сети и гибко управлять свойствами сети. Сеть может быть сохранена в виде .mat - файла. Богатый набор функций активации, алгоритмов обучения, функций тренировки, инициализации, предварительной и пост-обработки, а также ряд вспомогательных функций, делают Neural Network Toolbox универсальным инструментальным средством для решения задач в самых разных областях науки и техники, а также в экономических и финансовых приложениях.
Работа с пакетом может осуществляться как в режиме командной строки, так и в режиме графического интерфейса пользователя (GUI). В последнем случае доступна реализация только стандартных типов сетей. Сеть произвольной конфигурации можно реализовать только в режиме командной строки.
Архитектура сети наиболее распространенного типа - однонаправленной сети (feed-forward network) представлена на рис. 1(а,б). (На рис. 1б - схематическое изображение).
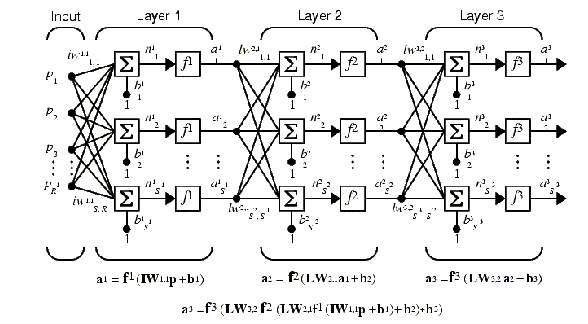
Рис.1a
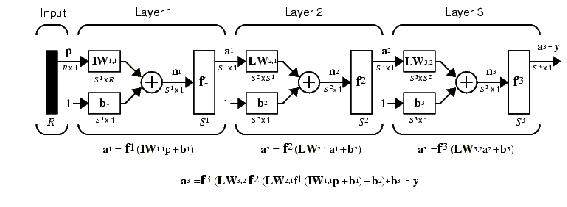
Рис.1б
Создадим сеть однонаправленную сеть для решения следующей модельной задачи.
Задан входной массив, состоящий из набора значений функции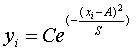 (S>0) на интервале (0,1). Создать нейронную сеть такую, что при вводе этих значений на вход сети на выходе получали бы значения параметров С,A и S.
В первую очередь необходимо определиться с размерностью входного массива. Выберем количество значений функции равным N=21, т.е. в качестве входных векторов массива используем значения функции yi в точках хi =0.05(i-1). Для обучения сети необходимо сформировать массив входных векторов для различных наборов параметров С,A и S. Каждый набор этих параметров является вектором-эталоном для соответствующего входного вектора.
Для подготовки входного и эталонного массивов воспользуемся следующим алгоритмом. Выбираем случайным образом значения компонент вектора - эталона С,A S и вычисляем компоненты соответствующего входного вектора. Повторяем эту процедуру М раз и получаем массив входных векторов в виде матрицы размерностью NxM и массив векторов - эталонов в виде матрицы размерностью в нашем случае 3хМ. Полученные массивы мы можем использовать для обучения сети.
Прежде чем приступать к формированию обучающих массивов необходимо определиться с некоторыми свойствами массивов.
Тестовый массив и массив эталонов подготовим с помощью программы:
P=zeros(100,21);
x=0:5.e-2:1;
for i=1:100
T(1,i)=0.9*rand+0.1; %Значение С
T(2,i)=0.9*rand+0.1; %Значение А
T(3,i)=0.9*rand+0.1; %Значение S
P(i,:)=T(1,i)*exp(-((x-T(2,i)).^2/T(3,i)));
end;
P=P';
С помощью этой программы формируется матрица P из M=100 входных векторов-столбцов, каждый из которых сформирован из 21 точки исходной функции со случайно выбранными значениями параметров C,A,S, и матрица T эталонов из 100 эталонных векторов-столбцов, каждый из которых сформирован из 3 соответствующих эталонных значений. Матрицы P и T будут использованы при обучении сети. Следует отметить, что при каждом новом запуске этой программы будут формироваться массивы с новыми значениями компонентов векторов, как входных, так и эталонных.
Вообще, выбор архитектуры сети для решения конкретной задачи основывается на опыте разработчика. Поэтому предложенная ниже архитектура сети является одним вариантом из множества возможных конфигураций
Для решения поставленной задачи сформируем однонаправленную трехслойную сеть, включающую 21 нейрон во входном слое (по числу компонент входного вектора) с передаточной функцией logsig, 15 нейронов во втором слое с передаточной функцией logsig и 3 нейрона в выходном слое (по числу компонентов выходного вектора) с передаточной функцией purelin. При этом в качестве обучающего алгоритма выбран алгоритм Levenberg-Marquardt (trainlm). Этот алгоритм обеспечивает быстрое обучение, но требует много ресурсов. В случае, если для реализации этого алгоритма не хватит оперативной памяти, можно использовать другие алгоритмы (trainbfg, trainrp, trainscg, traincgb, traincgf, traincgp,trainoss,traingdx). По умолчанию используется trainlm. Указанная сеть формируется с помощью функции newff:
net=newff(minmax(P),[21,15,3],{'logsig' 'logsig' 'purelin'},'trainlm');
Первый аргумент - матрица Mx2 минимальных и максимальных значений компонент входных векторов вычисляется с помощью процедуры minmax
Результатом выполнения процедуры newff является объект - нейронная сеть net заданной конфигурации. Сеть можно сохранить на диске в виде mat. файла с помощью команды save и загрузить снова с помощью команды load.
Следующий шаг - обучение созданной сети. Перед обучением необходимо задать параметры обучения. Задаем функцию ошибки sse.
net.performFcn='sse';
В этом случае в качестве ошибки вычисляется сумма квадратов отклонений выходов сети от эталонов
Задаем критерий окончания обучения - значение отклонения, при котором обучение будет считаться законченным:
net.trainParam.goal=0.01;
Задаем максимальное количество циклов обучения. После того, как будет выполнено это количество циклов, обучение будет завершено:
net.trainParam.epochs=1000;
Зададим периодичность вывода значений функции ошибок на график - 2. Значения функции ошибок будут наноситься на график через каждые две эпохи тренировки:
net.trainParam.show=2;
Теперь можно начинать обучение:
[net,tr]=train(net,P,T);
Процесс обучения иллюстрируется графиком зависимости функции ошибок от номера эпохи обучения:
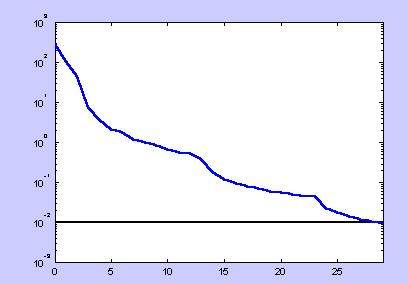
Рис.4
Таким образом обучение сети окончено. Теперь эту сеть можно сохранить в файле nn1.mat:
save nn1 net;
Для того, чтобы применить обученную сеть для обработки данных, необходимо воспользоваться функцией sim. В качестве входного вектора можно выбрать один из векторов, например p(:,25):
Y=sim(net,p(:,25));
Полученное значение Y должно быть близким к соответствующему эталону: T(:,25)
Перед тем, как воспользоваться нейронной сетью, необходимо исследовать обобщающую способность сети, т.е. убедиться в том, что сеть правильно работает с входными массивами, которые отличаются от того массива, на котором проводилось обучение. В качестве тестового массива необходимо использовать массив, компоненты которого отличаются от компонентов массива, использованного для обучения. В нашем случае для получения тестового массива достаточно воспользоваться еще раз программой mas1 .
Для оценки достоверности результатов работы сети можно воспользоваться результатами регрессионного анализа, полученными при сравнении эталонных значений со значениями, полученными на выходе сети, когда на вход поданы входные векторы тестового массива. В среде МАТЛАБ для этого можно воспользоваться функцией postreg. Следующий набор команд иллюстрирует описанную процедуру
mas1 %создание тестового массива P
y=sim(net,P); %обработка тестового массива
for i=1:3
figure(i);
[m,b,r]=postreg(y(i,:),T(i,:));
end;
Сравнение компонентов эталонных векторов с соответствующими компонентами выходных векторов сети
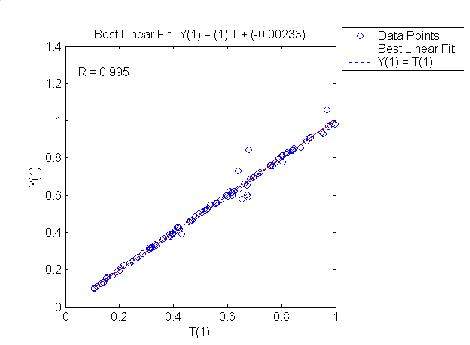
Рис.4
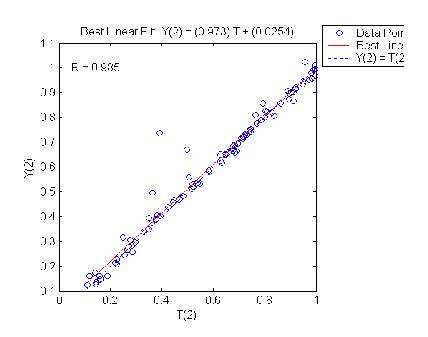
Рис.5
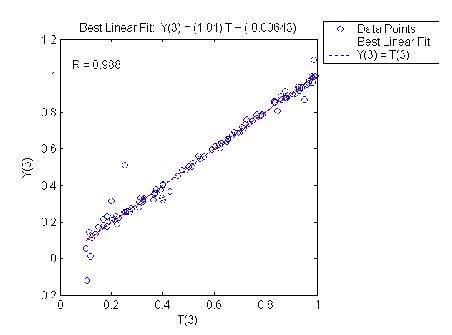
Рис.6
Все вышеизложенное можно выполнить с помощью графического интерфейса пользователя, который вызывается из командной строки командой nntool.