Титульный лист
Электронная библиотека
Автореферат магистерской работы
УНИВЕРСИТЕТ
: Донецкий национальный технический университет
СПЕЦИАЛЬНОСТЬ
: Технология машиностроения
КАТЕГОРИЯ РАБОТЫ
: Статья
АВТОРЫ
: Коваленко В. И., Кудрявцев А. А.
НАЗВАНИЕ
: ВЫРАВНИВАНИЕ ЭМПИРИЧЕСКИХ КРИВЫХ ПРИ ИССЛЕДОВАНИИ РАДИАЛЬНОГО БИЕНИЯ ВТУЛОК, ОБРАБОТАННЫХ НА ТОКАРНО-ВИНТОРЕЗНОМ СТАНКЕ С ЧПУ
СДЕЛАНО
: Донецк 2000
ОПУБЛИКОВАНО
:Инженер. Студенческий научно-технический журнал. - Донецк: ДонНТУ, 2000. №1.
E-MAIL:
nosko@ukrtop.com
В работе построены полигоны значений и проведено выравнивание эмпирических кривых.
Эмпирическая кривая распределения непрерывной случайной величины (полигон её значений) позволяет приближённо установить теоретический закон распределения исследуемой генеральной совокупности. Для более точного заключения эту кривую выравнивают и сопоставляют с предполагаемой теоретической кривой.
В условиях лаборатории кафедры “Технология машиностроения” Донецкого государственного технического университета была произведена окончательная обработка втулок на токарно-винторезном станке с ЧПУ модели 16К20Ф3 2Р22 проходными резцами, оснащенными пластинами из минералокерамики. На основании экспериментальных данных построены полигоны значений контролируемых величин, представленные на рисунках 1 и 2:
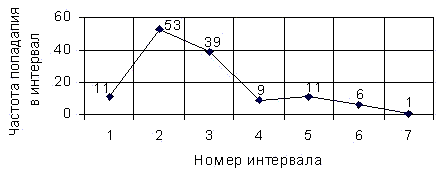
Рисунок 1 - Полигон значений величины радиального биения
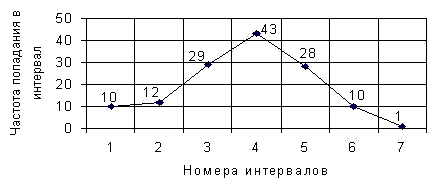
Рисунок 2 - Полигон значений величины диаметра заготовок
По виду полигонов можно предположить, что распределение плотности вероятности значений величины радиального биения подчиняется закону Релея, а распределение плотности вероятности значений величины диаметра заготовок – нормальному закону (закону Гаусса)
[1].
Выравнивание эмпирической кривой распределения предусматривает определение вероятности
 отдельных значений
отдельных значений  случайной величины Х или их частот на основании предварительно принятого (условного) теоретического закона распределения, параметры которого заранее неизвестны.
случайной величины Х или их частот на основании предварительно принятого (условного) теоретического закона распределения, параметры которого заранее неизвестны.
По внешнему виду полигона частот величины радиального биения было сделано предположение о подчинении кривой распределения закону Релея. Этот закон распределения часто используется при технологических исследованиях, так как ему подчиняется рассеивание погрешностей формы (овальность, конусообразность) и взаимного расположения поверхности (эксцентриситет, разностенность, непараллельность, перпендикулярность и т.д.).
Интегральная функция распределения Релея имеет вид
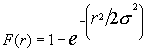 , (1)
Приняв в формуле (1)
, (1)
Приняв в формуле (1)  , получим следующую зависимость:
, получим следующую зависимость:
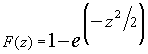 , (2)
Используя значения, полученные по формуле (2), можно рассчитать теоретические значения частости
, (2)
Используя значения, полученные по формуле (2), можно рассчитать теоретические значения частости 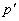 :
:
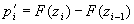 , (3)
Теоретические значения частоты попадания значений случайной величины в i-тый интервал:
, (3)
Теоретические значения частоты попадания значений случайной величины в i-тый интервал:
 , (4)
, (4)
где
N – объём выборки после исключения грубых ошибок, N=130.
Результаты расчётов по формулам (1)-(4) сведены в таблицу 1. Выровненная кривая, наложенная на полигон значений величины радиального биения, представлена на рисунке 4.
Таблица 1 – Результаты расчёта для построения теоретической кривой распределения значений величины радиального биения
|
Номер интервала, i |
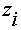
|

|

|
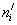
|
|
1 |
0,86 |
0,3091 |
0,3091 |
40 |
|
2 |
1,64 |
0,7394 |
0,4303 |
56 |
|
3 |
2,41 |
0,9452 |
0,2058 |
27 |
|
4 |
3,18 |
0,9936 |
0,0484 |
6 |
|
5 |
3,96 |
0,9996 |
0,0060 |
1 |
|
6 |
4,73 |
0,9999 |
0,0003 |
0 |
|
7 |
5,50 |
0,99999 |
0,00009 |
0 |
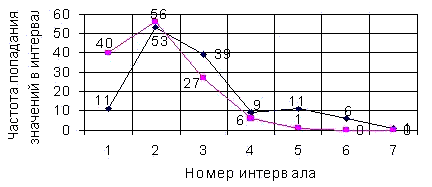
Рисунок 4 - Выравнивание эмпирической кривой по теоретическому закону:
◊- эмпирическая кривая; ■- теоретическая кривая.
Учитывая субъективность предварительной оценки, необходимо воспользоваться статистическими критериями согласия, например  - критерий Пирсона. Критерий
- критерий Пирсона. Критерий  наиболее приемлем при большом числе наблюдений, при любом теоретическом законе распределения исследуемых случайных величин, известных или неизвестных значениях его параметров. По сравнению с другими критериями он обеспечивает минимальную ошибку принятия неверной гипотезы [2].
наиболее приемлем при большом числе наблюдений, при любом теоретическом законе распределения исследуемых случайных величин, известных или неизвестных значениях его параметров. По сравнению с другими критериями он обеспечивает минимальную ошибку принятия неверной гипотезы [2].
Критерий Пирсона определяют по следующей формуле:
 , (5)
где
, (5)
где  ,
,  - соответственно экспериментальная и теоретическая частоты попадания в i – тый интервал;
- соответственно экспериментальная и теоретическая частоты попадания в i – тый интервал;
l – число интервалов.
Значение, рассчитанное по формуле (5), составляет  =130,02. Согласно таблице
=130,02. Согласно таблице  - распределения [2] теоретическое значение
- распределения [2] теоретическое значение  =11,07. Здесь
=11,07. Здесь  =0,05 – уровень значимости, f=l-r-1 – число степеней свободы; r – число оцениваемых параметров теоретической функции распределения Расчётное значение критерия Пирсона больше табличного. Это означает, что выдвинутая гипотеза о подчинении распределения значений величины радиального биения закону Релея ошибочна.
=0,05 – уровень значимости, f=l-r-1 – число степеней свободы; r – число оцениваемых параметров теоретической функции распределения Расчётное значение критерия Пирсона больше табличного. Это означает, что выдвинутая гипотеза о подчинении распределения значений величины радиального биения закону Релея ошибочна.
По внешнему виду полигона частот значений величины диаметра заготовки было сделано предположение о подчинении эмпирической кривой распределения нормальному закону. Закон нормального распределения приемлем для описания большого числа встречающихся на практике случайных величин. Это объясняется тем, что случайные величины могут рассматриваться как суммы большого числа независимых между собой слагаемых, каждое из которых имеет ничтожно малое влияние на всю сумму. При соблюдении этих условий суммарная случайная величина будет иметь распределение вероятностей, близкое к нормальному, независимо от того, каким законам распределения подчиняются её слагаемые. Соответствие нормальному закону распределения при этом будет возрастать по мере увеличения числа слагаемых.
Интегральная функция нормального закона распределения имеет вид:
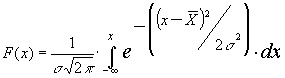 ,
,
где х – переменная случайная величина;
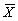 - среднее арифметическое значение случайной величины;
- среднее арифметическое значение случайной величины;
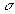 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Так как случайная величина Х в общем случае может принимать значения в пределах 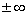 , то вероятность такого доверительного события равна
, то вероятность такого доверительного события равна
 ,
,
Вероятность же появления случайной величины Х в любом другом интервале меньше единицы и равна:
 ,
,
Решая данное уравнение, получим:
 ,
,
где 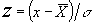 - новая переменная;
- новая переменная;
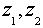 - новые пределы интегрирования.
- новые пределы интегрирования.
 - нормированная функция Лапласа [2]:
- нормированная функция Лапласа [2]:
 Эта функция нечётная, т.е.
Эта функция нечётная, т.е.  . Учитывая вышеприведенные преобразования, интегральный закон нормального распределения можно записать в виде:
. Учитывая вышеприведенные преобразования, интегральный закон нормального распределения можно записать в виде: 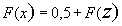 . Теоретические значения частости
. Теоретические значения частости 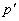 рассчитывается по следующей формуле:
рассчитывается по следующей формуле:
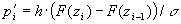 , (6)
где
, (6)
где 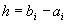 - ширина (шаг) интервала;
- ширина (шаг) интервала;
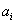 ,
, 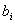 - границы i-го интервала;
- границы i-го интервала;
Теоретические значения частоты попадания значений случайной величины в i-тый интервал:
 , (7)
, (7)
где
N – объём выборки.
Результаты расчётов по формулам (6) и (7) сведены в таблицу 2. Выровненная кривая распределения, наложенная на полигон значений величины диаметра заготовки, представлена на рисунке 5.
Таблица 2 – Результаты расчётов для построения теоретической кривой распределения величины диаметра заготовки
|
Номер интервала, i |
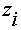
|

|
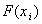
|

|
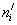
|
|
1 |
-2.14 |
-0.4838 |
0.0162 |
0.0127 |
2 |
|
2 |
-1.36 |
-0.4131 |
0.0869 |
0.0556 |
7 |
|
3 |
-0.57 |
-0.2157 |
0.2843 |
0.1551 |
21 |
|
4 |
0.21 |
0.0832 |
0.5832 |
0.2349 |
31 |
|
5 |
1.00 |
0.3413 |
0.8413 |
0.2028 |
27 |
|
6 |
1.79 |
0.4633 |
0.9633 |
0.0959 |
13 |
|
7 |
2.64 |
0.4959 |
0.9959 |
0.0256 |
3 |
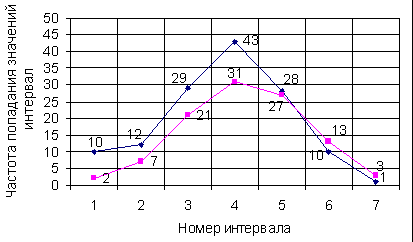
Рисунок 5 - Выравнивание эмпирической кривой по теоретическому закону:
◊
- эмпирическая кривая; ■- теоретическая кривая.
Согласно формуле (1) находим расчётное значение критерия Пирсона:
 =45,33. Согласно таблице
=45,33. Согласно таблице 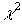 - распределение [2] теоретическое значение
- распределение [2] теоретическое значение 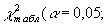
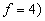 =9,49. Здесь
=9,49. Здесь  =0,05 – уровень значимости, f=l-r-1 – число степеней свободы; r – число оцениваемых параметров теоретической функции распределения (для нормального закона их два: среднее выборочное
=0,05 – уровень значимости, f=l-r-1 – число степеней свободы; r – число оцениваемых параметров теоретической функции распределения (для нормального закона их два: среднее выборочное 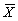 и стандартное отклонение
и стандартное отклонение 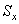 ). Расчётное значение критерия Пирсона больше табличного. Это означает, что выдвинутая гипотеза о подчинении распределения значений величины диаметра заготовки нормальному закону ошибочна.
). Расчётное значение критерия Пирсона больше табличного. Это означает, что выдвинутая гипотеза о подчинении распределения значений величины диаметра заготовки нормальному закону ошибочна.
Список литературы: 1. Шишкин И.Ф. Теоретическая метрология: Учебник для вузов. – М.: Изд-во стандартов, 1991. – 492 с., ил.
2. Моделювання й оптимiзацiя в машинобудуваннi: Навч. Посiбник / В.В. Душинський, С.Г. Кравченко. – К.: НМК ВО, 1992. – 304 с. – Рос. Мовою.
Титульный лист
Электронная библиотека
Автореферат магистерской работы


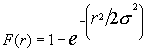 , (1)
Приняв в формуле (1)
, (1)
Приняв в формуле (1) 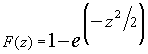 , (2)
Используя значения, полученные по формуле (2), можно рассчитать теоретические значения частости
, (2)
Используя значения, полученные по формуле (2), можно рассчитать теоретические значения частости 
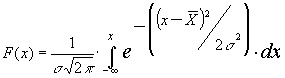 ,
, ,
, ,
, ,
, Эта функция нечётная, т.е.
Эта функция нечётная, т.е. 