Титульный лист
Электронная библиотека
Автореферат магистерской работы
УНИВЕРСИТЕТ
: Донецкий национальный технический университет
СПЕЦИАЛЬНОСТЬ
: Технология машиностроения
КАТЕГОРИЯ РАБОТЫ
: Статья
АВТОРЫ
: Коваленко В. И., Кудрявцев А. А.
НАЗВАНИЕ
: ИССЛЕДОВАНИЕ РАДИАЛЬНОГО БИЕНИЯ ВТУЛОК ПРИ ОБРАБОТКЕ НА ТОКАРНО-ВИНТОРЕЗНОМ СТАНКЕ С ЧПУ
СДЕЛАНО
: Донецк 2000
ОПУБЛИКОВАНО
:Инженер. Студенческий научно-технический журнал. - Донецк: ДонНТУ, 2000. №1.
E-MAIL:
nosko@ukrtop.com
В работе построены карты кумулятивных сумм.
В условиях лаборатории кафедры “Технология машиностроения” Донецкого государственного технического университета была произведена окончательная обработка втулок на токарно-винторезном станке с ЧПУ модели 16К20Ф3 2Р22 проходными резцами, оснащенными пластинами из минералокерамики. В ходе обработки производились выборки деталей. Начало каждой новой выборки определялось сменой пластины на чистовом резце. Периодические выборки позволяют судить об изменениях в налаженности технологического процесса. Результаты выборочного контроля иллюстрируются диаграммами, по оси абсцисс которых откладывают порядковый номер выборки, а по оси ординат – числовое значение контролируемого параметра. Такие диаграммы получили название простых контрольных карт. Пример одной из таких контрольных для величины радиального биения карт приведен на рисунке 1:

Рисунок 1 - Пример простой контрольной карты:
◊
- средневыборочные значения контролируемого параметра; ■- граница допуска
Недостатком простых контрольных карт является то, что они не накапливают измерительную информацию. Это делает их менее чувствительными к изменению контролируемого параметра.
Подобного недостатка лишены контрольные карты кумулятивных сумм. Построим контрольную карту кумулятивных сумм среднего арифметического величины радиального биения. В качестве исходных данных для расчёта зададимся::
1) номинальным значением параметра при налаженном технологическом процессе 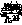 , равным половине допуска на величину радиального биения (
, равным половине допуска на величину радиального биения ( мм);
2) номинальным значением параметра при разлаженном технологическом процессе
мм);
2) номинальным значением параметра при разлаженном технологическом процессе  , равным величине допуска (
, равным величине допуска ( мм);
3) стандартным отклонением погрешностей величины радиального биения
мм);
3) стандартным отклонением погрешностей величины радиального биения  мм.
4) величины, связанные с вероятностями ошибок первого рода
мм.
4) величины, связанные с вероятностями ошибок первого рода  и второго рода
и второго рода 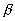 соответственно:
соответственно: 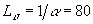 ;
; 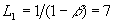 .
.
Определим степень разладки технологического процесса:
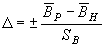 , (1)
Подставив имеющиеся численные значения величин в (1), получим
, (1)
Подставив имеющиеся численные значения величин в (1), получим 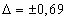 .
.
По заданным
 и
и 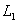 с помощью таблицы [1] находятся значения
с помощью таблицы [1] находятся значения 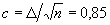 и t=2,98. Это даёт возможность определить
и t=2,98. Это даёт возможность определить 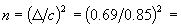
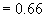 . Так как количество деталей – это число целое, то примем n=1.
. Так как количество деталей – это число целое, то примем n=1.
Граница регулирования определяется по формуле (2):
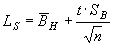 (2)
Подставив численные значения, получим
(2)
Подставив численные значения, получим  мм.
мм.
Предупредительная граница вычисляется по формуле (3):
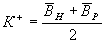 (3)
После подстановки численных значений получим
(3)
После подстановки численных значений получим  мм.
мм.
Контроль с помощью карты кумулятивных сумм среднего арифметического происходит следующим образом. Через определённые промежутки времени производятся выборки по
n изделий, у которых измеряется контролируемый размер. Как только одно из выборочных средних выйдет за какую-либо предупредительную границу, ему присваивается первый номер и начинается суммирование по формуле (4):
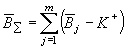 (4)
(4)
где
m – количество суммируемых выборок.
Если  , не достигнув границы регулирования, меняет знак, вычисление кумулятивных сумм прекращается и техпроцесс считается налаженным. После этого образование кумулятивных сумм возобновляется при очередном выходе
, не достигнув границы регулирования, меняет знак, вычисление кумулятивных сумм прекращается и техпроцесс считается налаженным. После этого образование кумулятивных сумм возобновляется при очередном выходе 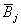 за предупредительную границу.
Если
за предупредительную границу.
Если  выходит за границу регулирования
выходит за границу регулирования  мм, то техпроцесс считается разлаженным и образование кумулятивных сумм прекращается до его наладки.
мм, то техпроцесс считается разлаженным и образование кумулятивных сумм прекращается до его наладки.
Вычисления для построения карты кумулятивных сумм удобно свести в таблицу (смотри таблицу 1). Карта кумулятивных сумм величины радиального биения приведена на рисунке 2.
На основании того, что кумулятивная сумма вышла за пределы границы регулирования, можно сделать вывод о разлаженности технологического процесса.
Таблица 1 – Вычисления для построения карты кумулятивных сумм величины радиального биения
|
Номер выборки |
J |
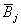
|

|

|
Комментарии |
|
1 |
1 |
0.053 |
0.023 |
+0.023 |
Начинается образование кумулятивной суммы, т.к. 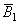 вышло за предупредительную границу вышло за предупредительную границу |
|
2 |
2 |
0.050 |
0.020 |
+0.043 |
|
|
3 |
3 |
0.045 |
0.015 |
+0.058 |
|
|
4 |
4 |
0.077 |
0.047 |
+0.105 |
|
|
5 |
5 |
0.073 |
0,043 |
+0,148 |
Принимается решение о прекращении образования кумулятивных сумм, т.к.  вышло за границу регулирования вышло за границу регулирования |
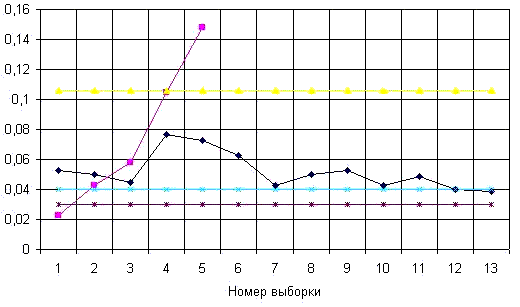
Рисунок 2 - Карта кумулятивных сумм величины радиального биения:
- - выборочные средние величины радиального биения;
- - кривая кумулятивной суммы;
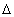 - граница регулирования
- граница регулирования  мм;
6
- величина допуска радиального биения
мм;
6
- величина допуска радиального биения 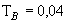 мм;
мм;
- - предупредительная граница
 мм.
мм.
При изучении технологических процессов и объектов часто возникает необходимость в проверке однородности выпускаемой продукции и качества функционирования самого процесса. Для решения этих задач можно воспользоваться статистическими методами проверки гипотезы о принадлежности исследуемых выборок к одной генеральной совокупности. Один из методов, с помощью которого можно сделать вывод о принадлежности нескольких выборок к одной генеральной совокупности, это метод проверки однородности дисперсий выборок. Для проверки однородности двух дисперсий на практике наиболее часто используется критерий Фишера. Этот критерий (
F – критерий) представляет собой отношение большей дисперсии к меньшей [2]:
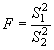 , (5)
, (5)
Расчётное значение критерия сравнивается с критическим табличным, определяемым для принятого уровня значимости и соответствующих
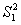 и
и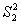 степеней свободы
степеней свободы 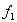 и
и 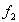 . Если расчётное значение
. Если расчётное значение 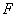 меньше табличного
меньше табличного , то дисперсии однородны и вместо
, то дисперсии однородны и вместо 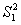 и
и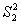 необходимо пользоваться средневзвешенным значением:
необходимо пользоваться средневзвешенным значением:
 (6)
Для облегчения расчётов характеристики выборок (объём выборки n, число степеней свободы f, среднее арифметическое
(6)
Для облегчения расчётов характеристики выборок (объём выборки n, число степеней свободы f, среднее арифметическое 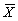 и оценку дисперсии
и оценку дисперсии 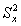 ) сведены в таблицу 2:
) сведены в таблицу 2:
Таблица 2 - Статистические характеристики выборок
|
Номер выборки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
N |
8 |
3 |
11 |
6 |
1 |
7 |
6 |
|
F |
7 |
2 |
10 |
5 |
0 |
6 |
5 |
|
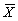 ,мм ,мм
|
0.0525 |
0.0500 |
0.0446 |
0.1067 |
— |
0.0786 |
0.0633 |
|
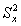 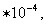
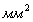
|
1,36 |
7,00 |
2,47 |
13,31 |
― |
26,86 |
7,47 |
Таблица 2 - Продолжение
|
Номер выборки |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
N |
5 |
7 |
15 |
22 |
15 |
14 |
14 |
|
F |
4 |
6 |
14 |
21 |
14 |
13 |
13 |
|
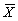 ,мм ,мм
|
0.0980 |
0.0500 |
0.0527 |
0.0468 |
0.0487 |
0.0400 |
0.0393 |
|
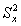 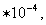
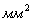
|
57,2 |
1,33 |
3,35 |
5,85 |
3,12 |
2,46 |
3,15 |
Первыми проверим на однородность самые большие выборки: 11 и 12. Расчётное значение критерия Фишера по формуле (10) 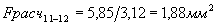 . Табличное значение критерия Фишера для степеней свободы
. Табличное значение критерия Фишера для степеней свободы 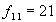 и
и 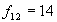
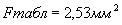 .
.
Итак, расчётное значение критерия меньше табличного. Значит, дисперсии однородны и необходимо заменить дисперсии выборок на средневзвешенную. Согласно формуле (6) средневзвешенная дисперсия
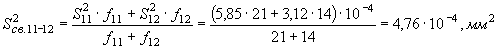
Число степеней свободы объединённой выборки  .
.
Аналогичным образом проводилась проверка однородности дисперсий остальных выборок. В результате получили две выборки. Статистические характеристики объединённых выборок приведены в таблице 3.
Таблица 3 - Сравнение статистических характеристик объединённых выборок
|
Выборка
(1-3,7,9-14) |
Выборка
(4,6,8) |
Вся совокупность
(без “чернот”) |
|
Количество элементов, n |
115 |
18 |
134 |
|
Выборочное среднее 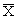 , мм , мм |
0,047 |
0,093 |
0,054 |
|
Дисперсия  |
3,69 |
21,65 |
8,63 |
|
Стандартное отклонение 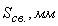 |
0,019 |
0,047 |
0,029 |
|
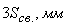
|
0,057 |
0,141 |
0,087 |
|
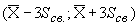
|
(0…0,105) |
(0…0,233) |
(0…0,142) |
Итак, четырнадцать выборок объединились в две. Причём одна из выборок вобрала в себя большую часть значений (115 из 134). Отсюда можно сделать вывод, что замена пластины резца не оказывает существенного влияния на исследуемый параметр. То есть пластины из минералокерамики марки _____ дают однородное рассеивание погрешностей радиального биения.
Для выявления взаимосвязи между факторами (диаметр и торцовое биение заготовки)и параметром (радиальное биение готовой детали) использован один из широко применяемых методов оценки статистических связей - корреляционный анализ. Он отвечает на вопросы: влияет ли данная величина на выходную и какова степень (теснота) связи между величинами?
Диаграммы рассеивания
[3] представлены на рисунках 3 и 4:
По диаграммам рассеивания можно судить о наличии и тесноте связи между величинами. Однако такая оценка субъективна. Объективно о тесноте связи между двумя переменными можно судить по величине коэффициента корреляции  [2]:
[2]:
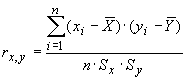 (7)
(7)
где п – количество пар значений величин х и у
;
 - оценки стандартного отклонения, мм.
- оценки стандартного отклонения, мм.
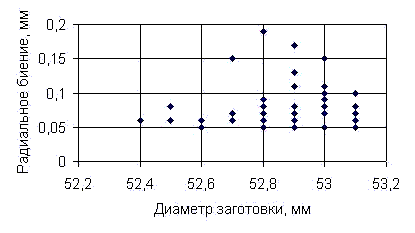
Рисунок 3 - Диаграмма рассеивания торцового и радиального биений

Рисунок 4 - Диаграмма рассеивания диаметра заготовки и радиального биения
Коэффициент корреляции может принимать значения от –1 до +1.
По формуле (7) определим
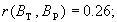
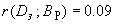 .
.
Оценки не равны нулю, но они далеки от крайних значений (-1;+1). Для определения статистической значимости полученного результата проверяется гипотеза о равенстве нулю оценки коэффициента корреляции [6]. В качестве критерия при проверке гипотезы используется случайная величина
 , (8)
, (8)
которая подчиняется распределению Стьюдента с
k=n-2 степенями свободы.
Проверим гипотезу о равенстве оценки коэффициента корреляции нулю для торцового и радиального биений. Согласно формуле (8) вычислим наблюдаемое значение случайной величины:
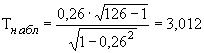
По уровню значимости
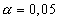 и числу степеней свободы k=126-2=124 находим из таблицы [6]
и числу степеней свободы k=126-2=124 находим из таблицы [6]  .
Так как
.
Так как 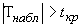 , то гипотезу отвергаем, т.е. оценка коэффициента корреляции статистически значима и между величинами торцового и радиального биений наблюдается линейная зависимость.
, то гипотезу отвергаем, т.е. оценка коэффициента корреляции статистически значима и между величинами торцового и радиального биений наблюдается линейная зависимость.
Однако оценка коэффициента корреляции также равна
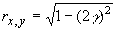 , (14)
где
, (14)
где 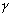 - относительная погрешность оценки коэффициента корреляции.
Отсюда
- относительная погрешность оценки коэффициента корреляции.
Отсюда 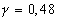 . То есть относительная погрешность значения оценки коэффициента корреляции составляет 48%. При такой погрешности результаты проверки гипотезы о равенстве оценки коэффициента корреляции нулю не следует принимать во внимание.
. То есть относительная погрешность значения оценки коэффициента корреляции составляет 48%. При такой погрешности результаты проверки гипотезы о равенстве оценки коэффициента корреляции нулю не следует принимать во внимание.
На основании вида диаграмм рассеивания и результатов расчётов можно сделать вывод о том, что величина радиального биения подвергается определённому воздействию каких то факторов, но эти факторы не были учтены при проведении данного эксперимента.
Список литературы: 1
. Шишкин И.Ф. Теоретическая метрология: Учебник для вузов. – М.: Изд-во стандартов, 1991. – 492 с., ил. 2. Справочник по теории вероятностей и математической статистике / Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 640 с. 3. Теория инженерного эксперимента: Учеб. пособие / Тимошенко Г.М., Зима П.Ф. – К.: УМК ВО, 1991. – 124 с. 4. Моделювання й оптимiзацiя в машинобудуваннi: Навч. Посiбник / В.В. Душинський, С.Г. Кравченко. – К.: НМК ВО, 1992. – 304 с. – Рос. Мовою. 5 Шишкин И.Ф. Контроль: Учеб. пособие. – СПб.: СЗПИ. 1992. – 62 с. 6. Микулик Н.А., Рейзина Г.Н. Решение технических задач по теории вероятностей и математической статистике: Справ. Пособие. – Мн.: Выш. шк., 1991. – 164 с.: ил.
Титульный лист
Электронная библиотека
Автореферат магистерской работы
![]()
![]()
![]()

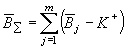 (4)
(4)

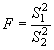 , (5)
, (5)
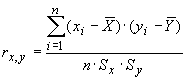 (7)
(7)


 , (8)
, (8)