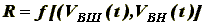 (1)
(1)Usage of the model estimation of the possible damage degree of details of the rolling mill manipulator on the design stage. In the article is reviewed the method of application of the model estimation degree damage the details of the rolling mill manipulator, during the time of improvement its design. The order of determining of the details parameters is reviewed also. The efforts which are operational on a vertical roller of the manipulator are determined.
На современном этапе развития производства, совершенствование существующего металлургического оборудования, должно происходить с учетом снижения его материалоемкости, повышения долговечности и обеспечения требуемого уровня производительности.
Для решения этих задач, с точки зрения оптимизации и обеспечения надежного их функционирования, процесс проектирования нового оборудования необходимо осуществлять с учетом оценки реальных нагрузок, действующих на него.
Учет рабочих нагрузок и усилий, воздействующих на детали, как внешних факторов VВШ(t), а также прочностных и геометрических характеристик деталей, представленных их параметрами, как внутренних факторов VВН(t), позволяет при вероятностном расчете их долговечности, использовать на стадии проектирования модель оценки степени возможных повреждений детали, представленную в работе [1], общий вид которой учитывает данные факторы:
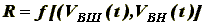 (1)
(1)где R - оценка степени возможных повреждений детали;
VВШ(t) - внешние факторы, действующие на деталь;
VВН(t) - внутренние факторы, влияющие на скорость накопления повреждений;
t - время эксплуатации детали.
Однако для более точной оценки долговечности деталей необходимо при проектировании определить перечень реальных нагрузок и оценить характер их воздействия на процесс накопления повреждения. Немаловажное значение такой подход имеет при проектировании совершенствовании машин, подвергающихся интенсивным перегрузкам и расположенным в технологической линии прокатного производства. Надежность работы таких машин сказывается на производительности прокатного стана, а значит, эффективность производства.
Эффективности работы прокатной клети зависит от оптимизации процесса прокатки, сказывающейся на производительности прокатного стана. На сегодняшний день, данная задача практически решена: выбрана оптимальная калибровка прокатных валков, определена скорость прокатки, назначены режимы обжатия и т.д. Одним из оставшихся методов повышения производительности прокатного стана, является принудительная задача металла в валки.
Чтобы осуществить такую процедуру, необходимо совершенствовать конструкцию манипулятора, который задавал бы дополнительное ускорение слитку, за счет встроенных вертикальных приводных роликов. Обеспечивая, таким образом, возможность увеличения обжатия в пропуске, а значит, повышение производительности прокатного стана.
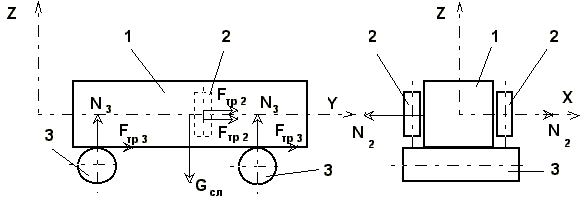
Как известно, максимальное ускорение aMAX, которое может быть достигнуто при горизонтальных роликах рольганга 3 (рисунок 1), не превосходит fg, что при коэффициенте трения слитка о ролики рольганга f=0,3 , составляет aMAX = 2,94 м/с2. Реально же данное значение еще меньше, и составляет для разных станов: a = 0,65 - 1,55 м/с2 [2].
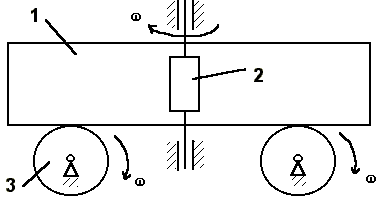
С целью увеличения ускорения слитка 1, предлагается установить дополнительные приводные вертикальные ролики 2, встроенные в линейку манипулятора [3]. Определим необходимую силу прижатия вертикального ролика к слитку N2 при заданной величине ускорения слитка. При расчете будем предполагать, что слиток находится на двух горизонтальных роликах и прижимается двумя вертикальными роликами с противоположных сторон, что всегда будет иметь место (рисунок 2).
Движение слитка описывается уравнением:
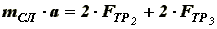
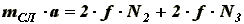 (2)
(2)где mСЛ - масса слитка; a - ускорение слитка; N2 - сила давления вертикального ролика на слиток; N3 - сила давления слитка на горизонтальный ролик рольганга (GСЛ=2*N3 , где GСЛ - вес слитка);
f - коэффициент трения слитка о горизонтальные и вертикальные ролики.
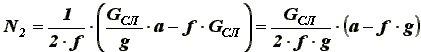 (3)
(3)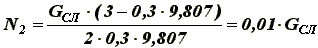
т. е. при весе слитка GСЛ = 100000 Н, сила давления вертикального ролика на слиток - N2 = 1000 Н. По формуле (3) строим номограмму для определения N2, в зависимости от f и a (рисунок 3).
Данные для построения при весе слитка GСЛ = 100000 Н, представлены в таблице.
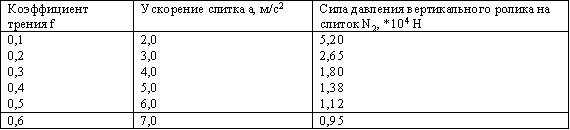
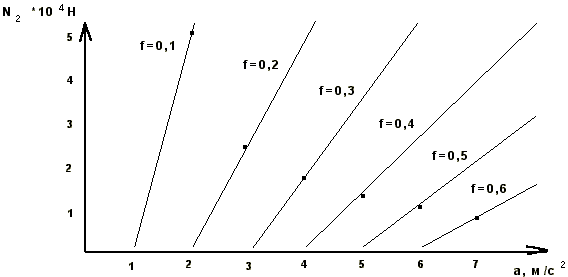
Представленная на рисунке 3 номограмма позволяет найти при известном коэффициенте трения f слитка о приводной вертикальный ролик и заданном ускорении а - необходимую силу прижатия N2 вертикального ролика к слитку. Сила N2 будет являться внешним ктором VВШ(t), определяющим степени повреждения деталей в совершенствуемой машине на стадии эксплуатации, или вероятностное значение долговечности деталей, на стадии проектирования. Оценить вероятностное значение долговечности проектируемой или совершенствующейся металлургической машины можно на основании имеющихся данных о предстоящей ее загрузке, т.е. имея информацию о планируемой производительности (производственной программе). Влияние внутренних факторов VВН(t) на степень повреждения деталей, определяется их прочностными и геометрическими характеристиками. Для определения их численного значения, необходимо используя расчетную схему действия нагрузок, рассчитать допускаемые напряжения в деталях машины. Опоры вертикальных роликов, в процессе работы прокатного стана, подвергаются интенсивным динамическим нагрузкам, вследствие взаимодействия ролика со слитком при выходе последнего из клети, поэтому необходимо рассчитывать упругий элемент опоры вертикального ролика на ударную нагрузку.
Расчетная схема вертикального ролика может быть представлена одномассовой упругой системой, на которую действует ударный импульс S (рисунок 4).
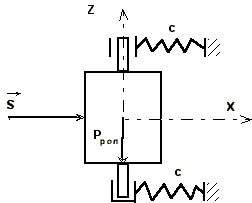
Рассмотрим свободные колебания системы, вызываемые ударным импульсом S. Пусть этот импульс прикладывается в течение бесконечно малого промежутка времени t (время удара), поэтому сразу после исчезновения импульса перемещение ролика будет еще отсутствовать, т.е.:
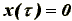 (4)
(4)На основании основного уравнения теории удара [4], вследствие приложения ударного импульса S, ролик мгновенно приобретет скорость:
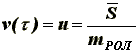 (5)
(5)где mРОЛ - масса вертикального ролика.
Условия (4) и (5) являются начальными условиями свободных колебаний системы, которые будут происходить после удара, т.е. при t > t.
Дифференциальное уравнение свободных колебаний системы имеет вид:
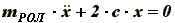 (6)
(6)где с - коэффициент жесткости упругих элементов в закреплении оси ролика.
Решением уравнения (6) с учетом начальных условий (4) и (5) будет:
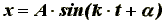
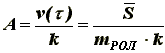
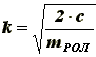
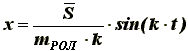 (7)
(7)При расчете упругого элемента ролика нас интересует максимальное смещение ролика, т.к. пружины, закрепляющие его ось, должны быть подобраны таким образом, чтобы не происходило касание их витков, следовательно, жесткость пружин должна определяться из условия:
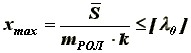
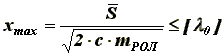 (8)
(8)Таким образом, из условия (8) находим необходимый коэффициент жесткости с пружины при заданном лябда0 , т.к. лямбда0 определяется из конструктивных соображений [4]:
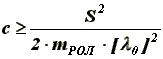 (9)
(9)Для расчета жесткости пружин опор вертикальных роликов по формуле (9) необходимо знать величину ударных импульсов, действующих на ролики. Рассмотрим взаимодействие слитка с вертикальными роликами при выходе слитка из клети (рисунок 5). За расчетный принимается случай, когда слиток взаимодействует с вертикальными роликами при не полном выходе слитка из клети, т.к. при этом не происходит затрат кинетической энергии слитка на поворот его во время удара.
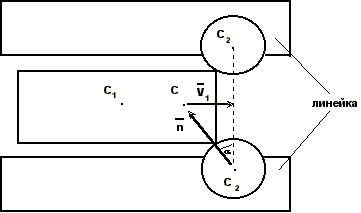
Рассматривая слиток и ролики как единую механическую систему, можно утверждать, что центр инерции С системы сохраняет величину и направление скорости после удара, т.к. все удары происходят внутри системы, т.е. возникают между телами, входящими в систему, а поэтому справедлив закон сохранения движения центра масс системы.
Скорость центра инерции С определяется из соотношения:
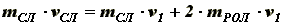 (10)
(10)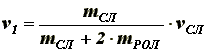 (11)
(11)Рассматривая скорость центра инерции С, как скорость движения преграды [4], о которую ударяется каждое из рассматриваемых тел, и применяя теорему об изменении количества движения к одному из роликов в проекции на направление нормали n при неупругом ударе, получим значение ударного импульса:
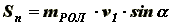
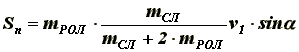 (12)
(12)Следует отметить, что определяя Sn при неупругом ударе, мы тем самым в неявном виде предполагаем, что, коэффициент восстановления к = 0. Это предположение позволяет получить наибольшее значение ударного импульса. Так при отношении mСЛ / mРОЛ >= 5, кинетическая энергия в случае к = 0 больше, чем при к <> 0, а это означает, что величина ударного импульса, определяемая по формуле (12) - наибольшая. Определяем максимальное напряжение пружины при принятых по конструктивным соображениям параметрам пружины:
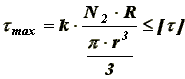 (13)
(13)где R - радиус витков пружины;
r - радиус проволоки;
k - коэффициент, учитывающий как влияние перерезывания, так и ряд других факторов, и величина которого зависит от соотношения R/r , при R/r=3 - k=1,58.
Полученную величину максимального напряжения сравниваем затем с допускаемым напряжением, которое с учетом изменяющейся нагрузки для рессорной стали равно [t] = 2/3 * 800 Н/мм2 = 540 Н/мм2.
Далее определяем осадку пружины и сравниваем ее с предельно допустимой осадкой:
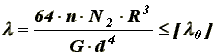 (14)
(14)где n - число витков пружины;
R - радиус витков пружины;
d - диаметр проволоки пружины;
G - модуль упругости при кручении.
После этого определяем для выбранной пружины осадку при воздействии ударного импульса по формуле:
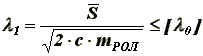 (15)
(15)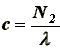
Если выбранные параметры пружины удовлетворяют условиям (13)-(15), то подбор пружины на этом заканчивается.
Теперь, имея значения внешних факторов VВШ(t), представленных силой N2, и внутренних VВН(t), представленных параметрами пружины: R, r, n, d, можно воспользоваться разработанной моделью оценки степени возможных повреждений детали [1], для определения ее вероятностного значения для деталей рассматриваемой машины, главным фактором которой будет являться ее производительность:
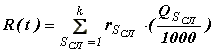 (16)
(16)где SСЛ - тип слитка (по весу), SСЛ = 1...k;
k - количество типов слитка;
QSсл - суммарная масса слитков типа SСЛ, пройденная через манипулятор за интервал времени t;
rSсл - удельное повреждение детали при воздействии на нее нагрузок от воздействия на нее 1000 тонн слитков типа SСЛ.
Таким образом, представленную модель достаточно легко адаптировать под любую металлургическую машину, что поможет обоснованно подойти к вероятностному определению степени вопреждения ее деталей не только во время эксплуатации, но и на стадии их проектирования.
1. Ченцов Н.А., Ручко В.Н. / Оценка использованной части ресурса деталей металлургического оборудования по усталостной прочности // "Защита металлургических машин от поломок", г. Мариуполь, 1998, С. 47-50.
2. Ф.К. Иванченко, П.И. Полухин, М.А. Тылкин, В.П. Полухин. "Динамика и прочность прокатного оборудования". М., "Металлургия", 1970, 487 с.
3. А.с. СССР № 452382 "Манипулятор-кантователь обжимного стана", 1974.
4. Н.В. Бутенин, Я.Л. Лунц, Д.Ф. Меркин. Курс теоретической механики. Т.2., М., "Наука", 1971, 462 с.