При разработке математической модели СГ во избежание слишком громоздких и сложных описаний применены следующие допущения: :
- отсутствуют потери в стали;
- воздушный зазор равномерен, магнитная проводимость одинакова и распределение магнитного поля в воздушном зазоре синусоидально;
- отсутствует влияние емкостей внутри и между обмотками;
- активное сопротивление не зависит от температуры;
- статор и ротор имеют трехфазные симметричные обмотки.
С целью наиболее полного отображения процессов, происходящих в синхронной машине как в переходных, так и в установившихся режимах работы, генератор целесообразно представить многоконтурной схемой замещения, в которой ротор представлен в виде нескольких параллельно включенных активно-индуктивных цепочек с постоянными параметрами
[].Для того, чтобы избежать периодических коэффициентов, зависящих от углового положения ротора, дифференциальные уравнения синхронного генератора записываются в осях
d, q, жестко связанных с его ротором. Для учета вытеснения тока массив ротора представляется k эквивалентными демпферными контурами по каждой из осей d, q и обмоткой возбуждения по оси d.ДУ, описывающие поведение СГ с многоконтурным ротором (
i=1,2,...,k), основываясь на [72], можно представить следующим образом:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
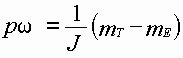 ,
,
![]() ,
,
![]() ,
,
где
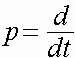
![]()
![]()
![]() - потокосцеплени статора, i-ого роторного контура СГ по осм d, q и потокосцепление обмотки возбуждени соответственно;
- потокосцеплени статора, i-ого роторного контура СГ по осм d, q и потокосцепление обмотки возбуждени соответственно;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - коэффициенты затухани контура статора, i-ого роторного контура, обмотки возбуждени по оси d и i-ого роторного контура по оси q:
- коэффициенты затухани контура статора, i-ого роторного контура, обмотки возбуждени по оси d и i-ого роторного контура по оси q:
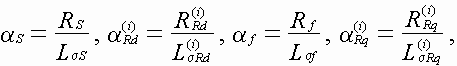
где
![]()
![]()
Потокосцепление ветви намагничивания:
![]() ,
,
![]() ,
,
где
![]()
 ,
,  ,
, 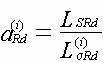 ,
,
 ,
, 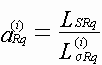 ,
,
где
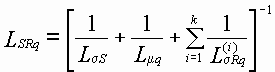 ,
,
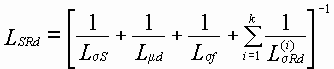 ,
,
где
![]()
Токи статора, обмотки возбуждения и
i-ого роторного контура: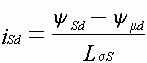 ,
,  ,
,  ,
,
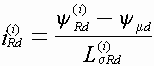 ,
, 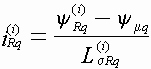 .
.
Уравнения для определения напряжения возбуждения, учитывающие тип возбудителя и автоматическое регулирование возбуждения (АРВ), являются частью математической модели СГ. С учетом действия форсировки возбуждения, уравнение для определения напряжения возбуждения генератора с системой самовозбуждения представлено как:
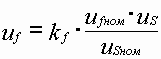 ,
,
где
![]()
![]()
![]()
![]()
Математическая модель синхронного двигателя
ДУ, описывающие поведение СД с многоконтурным ротором (
i=1,2,...,k), аналогичны уравнениям СГ, за исключением выражения для скорости вращения ротора, которое приобретает вид: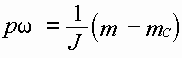 ,
,
где
![]()
Публикация: Сивокобыленко В.Ф., Меженкова М.А. Математическая модель электрической станции для анализа поведения турбогенераторов с системами самовозбуждения при коротких замыканиях // Технічна електродинаміка. Cпец. випуск за матеріалами II Міжнародної науково-технічної конференції “Математичне моделювання в електротехніці та електроенергетиці”. – Київ: Інститут електродинаміки НАН України. - 1998. – C. 100-105.