
Для оценки потерь при несинусоидальной периодической индукции, имеющей за период один минимум и одни максимум, удобен проверенный экспериментально метод [6-14]. Он основан на следующих допущениях:
1. Потери в стали состоят лишь из двух слагаемых - потерь на гистерезис и вихревые токи.
2. Потери на гистерезис за период не зависят от формы кривой индукции и определяются лишь двумя факторами: максимальным изменением (перепадом) индукции за период dВ = Вmax-Bmin и так называемой постоянной составляющей индукции Во = 0,5(Вmax+Bmin), где Bmin и Вmax - экстремальные значения средней по толщине листа индукции в стали.
3. Потери па вихревые токи пропорциональны квадрату действующего напряжения U2Д, индуктированного в обмотке.
4. В течение частей периода, когда индуктированное напряжение в обмотке отсутствует, никаких потерь в стали нет. Предполагается, что известны потери при синусоидально изменяющейся индукции любой нужной частоты и амплитуды, а также разделение потерь на гистерсзисные и вихревые согласно (0-11) или (6-12) и зависимость потерь от подмагничивания (от постоянной составляющей индукции). За базу для расчета принимаются потери рсин при синусоидальной индукции с таким же изменением индукции за полупсриод (2Bm=dВ) и, следовательно, с такими же ги-стсрсзпснымп потерями (РГ,СИН = РГ)| как и в реальном процессе. Изменение индукции определяется по среднему индуктированному напряжению

где t Bmin и t Bmax -пометы времени, соответствующие минимальном и максимальной индукции, откуда

Действующее напряжение, квадрату которого пропорциональны потери на вихревые токи, можно выразить через среднее напряжение и коэффициент формы кривой напряжения Rфи. Учитывая, что согласно (6-77) средине напряжения эквивалентной синусоиды и реальной кривой одинаковы: Ucp = Ucp син и что для синусоиды коэффициент формы =1,1
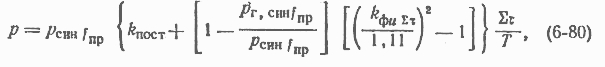
где все параметры с индексом "син" относятся к реальной частоте f.
При больших значениях Rфи т. е. при сильно искаженной кривой напряжения, скорость процесса синусоидального перемагничивания при частоте f значительно ниже скорости реального процесса. Это часто бывает при прерывистой кривой напряжения.
Если кривая напряжения прерывистая, т. е. участки времени т, в течение которых индукция в стали меняется, чередуются с участками, в течение которых напряжение отсутствует и индукция неизменна, то к рассматриваемому процессу ближе синусоидально-изменяющаяся индукция с периодом ЕТ, чем с периодом Т (рис. 6-13). Поэтому, используя допущение 4, рекомендуется ввести приведенную частоту fпр = fT/Eт , определить по характеристикам стали или по (6-12), (6-13) соответствующие этой частоте потери рсин и соотношение РГ,СИН /Р СИН при амплитуде индукции Вт и умножить результат, полученный по формуле (6-78), на долю времени Eт/T, в течение которого есть напряжение.
При этом расчете коэффициент формы кривой напряжения, определяемый только для периода Eт, оказывается заметно ближе к 1,11, чем при расчете его для периода Т, т. е. взятый за основу для пересчета режим с синусоидальной индукцией ближе к реальному режиму перемагиичивания стали.
Если напряженность или индукция магнитного поля содержит значительную постоянную составляющую, потери заметно больше, чем при се отсутствии. Приняв согласно допущению 3, что эта составляющая не влияет на потери от вихревых токов, вместо (6-78) получаем:
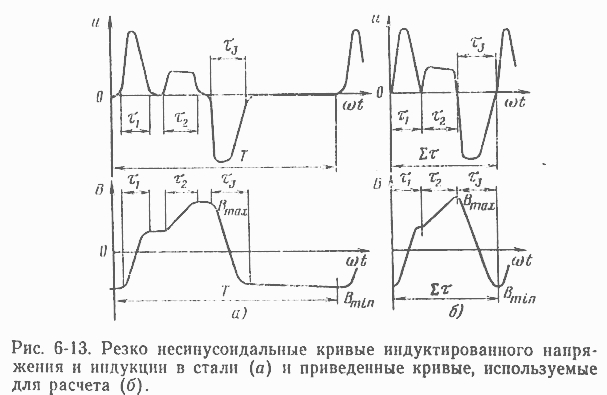
где Pсинfпр - потери при синусоидальной индукции Вт == dВ/2 и приведенной частоте fпр=1/Eт (вместо реальной частоты f=1/Т); Rпост - отношение потерь при наличии постоянного подмагничивания к потерям при его отсутствии в случае синусоидальной индукции с амплитудой Вт частотой fпр; RфиЕт- коэффициент формы кривой индуктированного напряжения за период Ет.
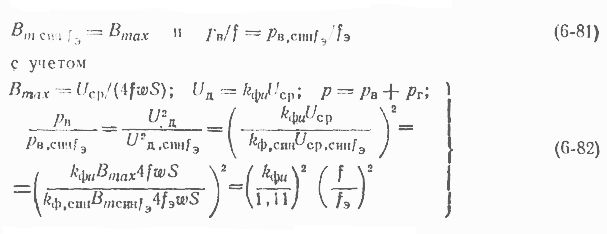
Для упрощенной оценки потерь при отсутствии постоянной составляющей можно использовать понятие "эквивалентная частота" fa. Это такая частота, при которой синусоидально меняющаяся индукция имеет такую же амплитуду, как максимальная рояльная индукция В max, и расчетные потери от вихревых токов за период при отсутствии вытеснения поля равны расчетным потерям за период при реальной кривой.
Тогда из условий
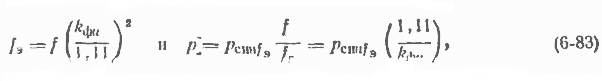
после алгебраических преобразовании следует
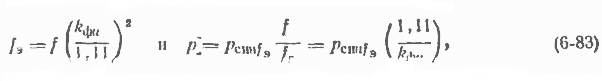
где f - реальная частота; kфи - коэффициент формы кривой реального (не приведенного) напряжения; Pcинfэ потерн при синусоидальной индукции, имеющей частоту fэ и амплитуду Вт. Подстановка fэ по (6-83) в аппроксимацию (6-13) и использование последней п выражении потерь (6-83) при сохранении индукции дают формулу, из которой особенно явно видно влияние несинусоидальности на потери в стали:

Если кривая индукции имеет несколько экстремумов за период, т. е. кривая напряжения несколько раз за период меняет знак, то для грубой оценки потерь можно: разделить реальную кривую индукции на несколько участков по времени (интервалов) между соседними экстремумами; принять, что потери за период равны сумме потерь на отдельных участках; считать, что потери на каждом участке за цикл такие же, как потери за цикл при многократном и непрерывном повторении кривой индукции, соответствующей этому участку, по с чередованием роста и уменьшения индукции. Тогда средние за период потери равны сумме потерь на отдельных участках, вычисленных по формуле (6-80). При этом остается относительно большой произвол в определении коэффициента кпост и метод может давать большую погрешность. Поэтому такую грубую оценку потерь можно рекомендовать только при невозможности экспериментального исследования макета или опытного образца изделия.
Таким образом, для определения потерь как при повышенной частоте, так и при несинусоидальной индукции желательно знать не только долю гистерезисных потерь, но и зависимость потерь от амплитуды индукции и от частоты для синусоидально изменяющейся индукции. Иногда такие данные приводят в каталогах на сталь. При отсутствии этих данных для оценок потерь можно использовать ориентировочные сведения, и формулы (6-13), а также выражение

где индекс "б" относится к Оазисной частоте, для которой в стандарте нормируются параметры стали данной марки.