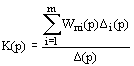 , (1)
, (1)УДК
62-83-52П.Х. Коцегуб, О.И. Толочко, В.Ю.Мариничев, П.И. Розкаряка
Определение передаточных функций систем
автоматического управления с наблюдателями состояния
П.Х. Коцегуб, О.И. Толочко, В.Ю.Мариничев, П.И. Розкаряка Определение передаточных функций системы автоматического управления с наблюдателем состояния // Сборник научных трудов ДонГТУ. Серия: Электротехника и энергия, вып.4: ДонГТУ, 1999г
Предложен метод упрощённого определения передаточных функций систем автоматического управления, замкнутых через наблюдатель состояния, по формуле Мейсона, основанный на учёте теоремы разделения. Рассмотрен пример, подтверждающий эффективность этого метода.
В современных электромеханических системах все чаще применяются наблюдатели состояния (НС) для восстановления не измеряемых координат объекта, которые по тем или иным причинам необходимы для построения желаемой системы управления
[1,2]. В результате этого система оказывается замкнутой, как правило, не только по измеряемым координатам объекта, но и по координатам, восстановленным при помощи наблюдателя.Для анализа систем с наблюдателями состояния весьма полезно знать передаточные функции по управляющему и возмущающему воздействиям.
Ряд приемов, облегчающих определение передаточных функций систем, описание которых выполнено в пространстве состояний, приведен в
[3]. Однако часто системы представлены в виде структурных схем с использованием передаточных функций отдельных элементов. В этом случае поставленная задача обычно решается с использованием формулы Мейсона, в соответствии с которой передаточная функция равна![]()
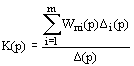 , (1)
, (1)
где
![]()
m
– число таких каналов; …, (2)
…, (2)
![]()
![]() ,
, ![]()
![]()
При наличии в системе НС весьма затруднительно находить
Для упрощения вычисления
![]() . (3)
. (3)
Можно показать, что при выполнении условия (3) справедливым будет и формула
![]() . (4)
. (4)
Выражения для
После подстановки (4) в (1) имеем следующее выражение для передаточной функции системы:
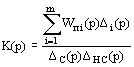 . (5)
. (5)
В связи с тем, что
Так например, для системы, представленной на рис.1, в которой восстанавливаются всего лишь две координаты
![]() ,
,
![]()
![]() , (6)
, (6)
произведение передаточных функций пар не соприкасающихся друг с другом разомкнутых контуров включает пять слагаемых
![]()
![]() , (7)
, (7)
и одно слагаемое имеет место для произведения передаточных функций троек не соприкасающихся друг с другом контуров
 . (8)
. (8)
Легко теперь представить, какое внимание должно быть проявлено при нахождении
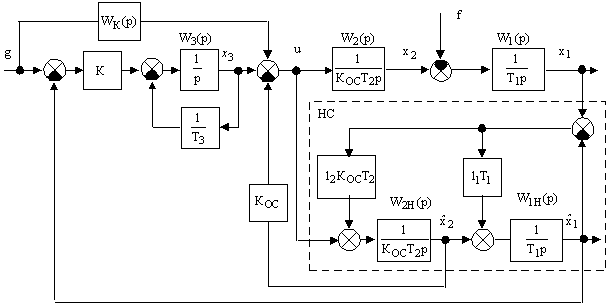
Рисунок 1 -- Система автоматического управления с наблюдателем состояния
Необходимо отметить и следующее положение, облегчающее вычисление передаточных функций. Если воздействие, по отношению к которому определяется передаточная функция, прикладывается к системе до точки съема управляющего сигнала
u наблюдателя состояния, то![]() . (9)
. (9)
Тогда, с учётом (5), передаточная функция системы с НС
 (10)
(10)
В последних двух уравнениях
Полученное выражение для передаточной функции (10) свидетельствует о том, что воздействия, приложенные к системе до управляющего сигнала наблюдателя
u, отрабатываются так же, как и системой, замкнутой по собственным координатам. Настройка наблюдателя состояния в этом случае не влияет на характер переходных процессов.Следует, однако, помнить, что приведенное выше утверждение справедливо только при нулевых или одинаковых начальных условиях координат системы
Необходимо отметить, что
Если воздействие прикладывается к системе после точки съема управляющего сигнала
u наблюдателя, то передаточная функция системы с наблюдателемРассмотрим применение изложенных выше положений и рекомендаций на примере определения передаточных функций системы, представленной на рис.1, по управляющему и возмущающему воздействиям:
![]() . (11)
. (11)
Структурная схема системы рис.1, замкнутой по собственным координатам, представлена на рис.2.
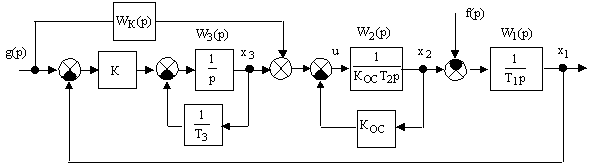
Рисунок 2
- Система автоматического управления, замкнутая по собственным координатамСтруктурная схема наблюдателя состояния выделена на рис.1. Для схемы на рис.2 и схемы НС, которые намного проще исходной системы с наблюдателем состояния, без затруднений находим
![]() (12)
(12)
и
![]() (13)
(13)
Выражение
Управляющее воздействие
g прикладывается к системе по двум каналам левее точки съема управляющего сигнала наблюдателя состояния. Поэтому передаточная функция системы с наблюдателем совпадает с передаточной функцией системы, замкнутой по собственным координатам (см.рис.2). Из рис.2 с учетом (10) находим ![]() , (14)
, (14)
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
а
Возмущающее воздействие
f прикладывается к системе после точки съема управляющего сигнала наблюдателя. По этой причине передаточная функция системы![]() , (15)
, (15)
где
![]()
![]()
![]() - (16)
- (16)
выражение, составленное по правилу (2) для контуров, не касающихся прямого пути с передаточной функцией
W1(p).После подстановки в (15) значений
![]()
![]()
![]()
окончательно получаем следующее выражение для передаточной функции системы по возмущающему воздействию
:![]() (17)
(17)
где
Наличие нуля в точке
p=0 у передаточной функцииИные особенности работы рассматриваемой системы с наблюдателем состояния не являются предметом исследования настоящей статьи.
Выводы
ЛИТЕРАТУРА
1. Кузовков Н.Г. Модальное управление и наблюдающие устройства. М.: Машиностроение, 1976.-184 с.
2. Акимов Л.В., Долбня В.Г., Колотило В.И. Системы управления электроприводами постоянного тока с наблюдателями состояния. – Харьков: ХГПУ. 1998. –117 с.
3. Толочко О.И., Коцегуб П.Х., Федоряк Р.В. Анализ линейных систем с наблюдателями состояния // Вестник Харьковского политехнического института. –2000.- Выпуск 113. – с.78-81.
![]()