УДК 62-83-52
АНАЛИЗ И СИНТЕЗ МОДАЛЬНЫХ СИСТЕМ,
ЗАМКНУТЫХ ЧЕРЕЗ НАБЛЮДАТЕЛЬ СОСТОЯНИЯ ПОЛНОГО ПОРЯДКАТолочко О.И., Коцегуб П.Х., Федоряк Р.В.
Донецкий государственный технический университет
Толочко О.И., Коцегуб П.Х., Федоряк Р.В. Анализ и синтез модальных систем замкнутых через наблюдатель состояния / Сборник научных трудов ДонГТУ. Серия: Электротехника и энергия, вып.5: ДонГТУ, 2000г
olga@pandora.kita.donntu.ru
Analisys of modal control systems, which confined across the full order state observer, has carried out. The method of system transfer function definition was suggested with help of transfer functions of system, confined on proper state variables, and observer's transfer function. It was proved the appropriateness of using the symbol mathematic software for analisys and sinthesys such kind of systems.
Рассмотрим систему модального управления (СМУ), замкнутую через наблюдатель состояния (НС) полного порядка, структурная схема которой показана на рис.1, где
u – управляющее воздействие; f – возмущающее воздействие; Ao, Bo, Bf, Co, Aн, Bн, Cн – матрицы состояния, управления, возмущения и выхода объекта регулирования (ОР) и наблюдателя соответственно; K=[k1 k2 ... kn] – коэффициенты передачи модального регулятора (МР); L=[l1 l2 ... ln]Т – коэффициенты НС.В
[1] показано, что при полной идентичности разомкнутых ОР и НС![]() ;
; ![]() ;
; ![]() , (1)
, (1)
математическое описание системы рис.1 можно преобразовать к виду:

где
–
вектор ошибок оценивания НС,
–
матрицы состояния СМУ, замкнутой через НС, СМУ, замкнутой по собственным переменным состояния, и наблюдателя состояния соответственно.На основании анализа клеточной матрицы
Аз иногда делают вывод о том, что замкнутая система с одним регулятором состояния является более быстродействующей, чем система, замкнутая через наблюдатель, поскольку характеристический полином СМУ с НС полного порядка Gз равен произведению характеристических полиномов СМУ без НС Gоз и НС Gнз:![]()
Однако в общем случае быстродействие и другие показатели качества переходных процессов зависят не только от полюсов передаточной функции (ПФ), но и от ее нулей. В связи с этим определим матричную ПФ исследуемой СМУ от управляющего и возмущающего воздействий до вектора состояния:

Воспользовавшись формулой обращения клеточной матрицы
[2], получим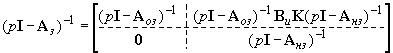
После подстановки (7) в (6) и перемножения матриц имеем:


Из (8) видно, что ПФ СМУ, замкнутой через НС, от управляющего воздействия до переменных состояния объекта регулирования
Wxu(p) совпадает с соответствующей ПФ СМУ без НС Wxuo(p):![]()
а ошибки оценивания НС при отработке управляющего воздействия тождественно равны нулю. Сопоставляя характеристический полином
ПФ (9) с полиномом (5), приходим к выводу, что передаточные функции СМУ с НС полного порядка по управляющему воздействию содержат в числителе характеристический полином наблюдателя, который сокращается с таким же полиномом в знаменателе.При отработке возмущающего воздействия поведение вектора ошибок оценивания D
X определяется передаточной функцией Wxfн(p) НС, к которому приложено возмущающее воздействие![]()
а поведение координат объекта зависит как от параметров объекта, так и от параметров наблюдателя.
Анализируя правую верхнюю клетку матрицы (8), можно записать:
![]()
где
![]() (12)
(12)
– передаточная функция наблюдателя от приложенного к нему возмущающего воздействия до суммарного сигнала обратной связи модального регулятора.
Умножая обе части уравнения (11) на вектор выхода
С слева, получим ПФ системы от возмущающего воздействия до выходного сигнала:![]()
Следовательно, любая передаточная функции СМУ с НС полного порядка по возмущающему воздействию равна сумме соответствующей передаточной функции СМУ без НС по возмущающему воздействию и произведения передаточной функции СМУ без НС по управляющему воздействию и передаточной функции наблюдателя от возмущающего воздействия, приложенного к НС, до суммарного сигнала обратной связи модального регулятора.
Формулы (11), (13) и (14) дают возможность упростить вывод передаточных функций СМУ с наблюдателем полного порядка за счет использования вместо исходной структурной схемы с большим количеством перекрестных связей более простых расчетных структурных схем СМУ без НС и НС без СМУ.
Попробуем воспользоваться уравнением (13) для оценки статизма по нагрузке системы тиристорный преобразователь-двигатель постоянного тока (ТП-Д) с компенсацией внутренней обратной связи по ЭДС двигателя с модальным регулятором, рассмотренную в
[3]. Структурная схема этой системы в относительных единицах представлена на рис.2. Здесь возмущающим воздействием является ток нагрузки f=Iс*, управляющим – задание на скорость двигателя u=w з*, переменными состояния – скорость двигателя, ток якоря и ЭДС преобразователя X=[w * I* Eп*], выходной координатой – скорость двигателя y=w *, C=[1 0 0].Расчетные структурные схемы представлены на рис.3а,б.
Из схемы рис.3а

 ; (14)
; (14)
из схемы рис.3б
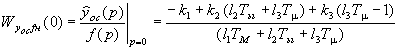 . (15)
. (15)

Рисунок 2
а) б)
Рисунок 3
Используя формулу (13) при
p=0 с учетом (14) и (15), имеем:

Разделив обе части уравнения (1
6) на первое слагаемое, получим выражение для отношения падения скорости в СМУ с НС D w с* к падению скорости в СМУ без НС D w со*:

Аналогичным образом можно определить и соответствующие передаточные функции. Однако, несмотря на некоторое облегчение этого процесса при помощи выше изложенной методики, существенную помощь можно получить только при использовании ЭВМ.
В настоящее время многие программные пакеты обладают способностью решать математические задачи в аналитическом виде. Из них в наибольшей степени для исследования и проектирования САУ приспособлена система
MATLAB 5 [4], которая имеет в своем составе пакет прикладных программ символьной математики Symbolic Toolbox, инструментарий для анализа и синтеза линейных систем Control Toolbox, приложение для структурного математического моделирования Simulink и многие другие полезные функции. В состав пакета Symbolic Toolbox включено ядро мощной системы символьных вычислений MAPLE V.Рассмотрим возможность применения вышеназванных программных средств для синтеза МР и НС системы рис.2 и для анализа влияния отношения среднегеометрических корней характеристических полиномов СМУ, замкнутой по собственным переменным состояния, и наблюдателя
(W 0 и W н).Перечислим основные функции, которые могут быть использованы при решении поставленной задачи:
syms var1 var2 ...varN – объявление символических переменных;
G = poly (A, p) – формирование характеристического полинома системы G по ее матрице состояния A в функции символической переменной p;
Ac = ctrb (A, B) – формирование матрицы управления;
Ao = obsv (A, C) – формирование матрицы наблюдения;
Ai = inv (A) – обращение матрицы;
At = A’ – транспонирование матрицы;
[num, den] = ss2tfm (A, B, C, D, iu) – формирование коэффициентов полиномов числителя num и знаменателя den передаточной функции системы по i - му входному сигналу, исходя из описания системы в пространстве состояний (матрицы A, B, C, D);
expr1 = collect (expr, var) – приведение подобных в выражении expr по переменной var;
expr1 = subs (expr, var, var1) – подстановка в символическое выражение expr вместо переменной var подвыражения, присвоенного предварительно переменной var1;
var = eval (expr) – вычисление символического выражения.
Листинг решения поставленной задачи с помощью системы MATLAB, имеет вид:
K =
[ (Tmu+w0^3*Tm*Ta^2*Tmu)/Ta,
Tmu*(Tm+a2*w0^2*Tm*Ta^2-Ta-Tm*a1*w0*Ta)/Tm/Ta,
(a1*w0*Ta*Tmu-Ta-Tmu)/Ta]
L =
[ a1*wn-1/Tmu-1/Ta]
[Tm*(a2*wn^2-1/Tm/Ta-1/Ta/Tmu)-Tm*(Ta+Tmu)/Tmu/Ta*(a1*wn-1/Tmu-1/Ta)]
[ Tm*Ta*(wn^3-(1-kke)/Ta/Tm/Tmu)-1/Tmu*Tm*Ta*(a2*wn^2-1/Tm/Ta-1/Ta/Tmu)+
+1/Tmu^2*Tm*Ta*(a1*wn-1/Tmu-1/Ta)]
dWc0 =
-a2/Tm/w0+1/Ta/Tm^2/w0^3
dWc =
(-1 + (1/Tmu/w0-a1+1/w0/Ta)*a2/kw +
+((-a1*a2/Tmu+a1^2/w0/Tmu-a1/w0^2/Tmu^2)-a1/w0^2/Ta^3+
+(a1^2/w0-a1/w0^2/Tmu)/Ta+a1/w0^2/Ta/Tm)/kw^2+
+((a2/w0/Tmu+1/w0^3/Tmu^3-1-a1/w0^2/Tmu^2)+1/w0^3/Ta^3+(-a1/w0^2+1/w0^3/Tmu)/Ta^2+
+(a2/w0+1/w0^3/Tmu^2-a1/w0^2/Tmu)/Ta+((a1/w0^2-2/w0^3/Tmu)/Ta-2/w0^3/Ta^2)/Tm)/ kw^3)/
/Tmu/Ta/Tm/w0^3
Здесь обозначено:
Ta® Tя , Tm® Tм , Tmu® Tm , w0® W o , wn® W н , kw® kW =W н/W o , dWc0® D w co*/Ic*, dWc® D w c*/Ic*, a1, a2 ® a 1, a 2 – коэффициенты нормированного полинома третьего порядка![]()
принятого в качестве желаемого для характеристических полиномов СМУ и НС, которые в данном случае будут отличаться друг от друга только значением среднегеометрического корня W
.Во второй части программы выполнена подстановка в символьные выражения конкретных значений, в результате чего получены графики зависимостей D w
co / D w c от kW при разных значениях Tя и Tм, представленные на рис.4 а, б (a 1 = a 2 = 2 – фильтр Баттерворта).Графики рис.4 имеют один “ноль” и два экстремума: максимум и очень сглаженный минимум, которые можно найти при помощи
MATLAB-функций diff (expr, var), выполняющей дифференцирование выражения expr по заданной переменной var, и solve (expr), определяющей корни уравнения expr(var)=0. Из графиков видно, что в большом диапазоне параметров статизм СМУ, замкнутой через наблюдатель (рис.2), оказывается ниже, чем аналогичной системы без НС (рис.3а), причем при некотором значении kW , близком к 1, анализируемая система становится астатической.Для подтверждения правильности полученных результатов на рис.5 приведены графики переходных процессов тока и ошибки по скорости при набросе номинальной нагрузки в СМУ с
Tя=4Tm , Tм=8Tm , W o=0.5/Tm . Штрих-пунктиром показаны переходные процессы в СМУ, замкнутой по собственным координатам, а сплошными линиями – в системе с НС при значениях коэффициента kW , обеспечивающих нулевую (графики 1) и экстремальные (графики 2, 3) величины статического падения скорости. Из рисунка видно, что замыкание СМУ через наблюдатель полного порядка при данных параметрах привода приводит к снижению статического и динамического падения скорости, к увеличению перерегулирования по току и к уменьшению времен достижения током и скоростью максимальных значений.а) б)
Выводы
Следует отметить, что приведенные выводы справедливы и в том случае, когда управляющее и возмущающее воздействия являются не скалярными, а векторными сигналами. Указанное ограничение введено в систему рис.1 только для упрощения понимания и обеспечения большей наглядности.
Литература
Analysis and synthesis of modal systems, confined across the full range state observer.