МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ И МОДЕЛИРОВАНИЕ АД

 В ТРЕХФАЗНОЙ СИСТЕМЕ КООРДИНАТ

 

Уравнение электрического равновесия цепей статора и ротора для мгновенных значений сигнала, записанные в векторной форме имеют следующий вид:

 

         

 

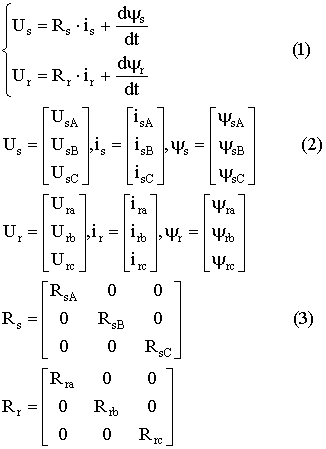
При условии симметричности фаз можно записать:

 

 

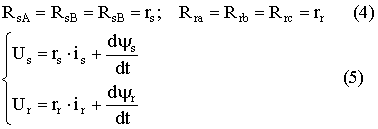
При ненасыщении магнитной цепи машины потокосцепление фаз статора и ротора выражается через токи фаз статора и ротора при помощи выражения:

 

Для примера 1-е уравнение системы (6) имеет вид:

 

При условии симметричности воздушного зазора, синусоидальности МДС и приведения всех величин к обмотке статора, можно записать:

 

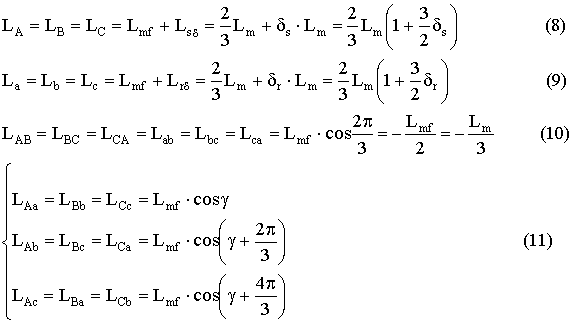
- это индуктивность фазы статора от основного магнитного потока и максимальная взаимоиндуктивность разных фаз статора и ротора, имеющая место при совпадении их магнитных оси

- это индуктивность ветви намагничивания 1-фазной схемы замещения АД в установившемся режиме.

          - коэффициенты рассеяния статора и ротора

          Z_p- количество пар полюсов

          φ- угол поворота ротора

ω- механическая скорость ротора

Z_p- скорость, приведенная к скорости вращения эемагнитного поля статора.

Обозначим:

Тогда с учетом (8) и (12) общая матрица взаимных индуктивностей:

 

 

Тогда систему уравнений (6) можно записать в объединенной форме следующим образом:

 

Из (18) следует, что зная вектор потокосцепления, вектор токов можно определить, решая систему линейных уравнений:

 

 

Электромагнитная  энергия 3-х фазной машины определяется выражением:

Момент:

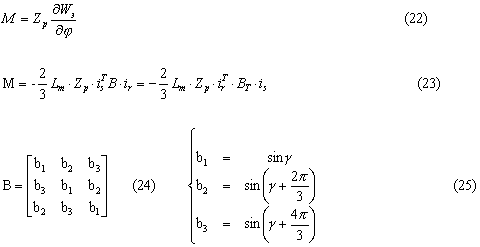
Избежать наличия гармонических элементов в формуле электромагнитного момента можно, заменив вектор тока статора через вектор тока и потокосцепления ротора

 

В развернутом виде формула (26) имеет следующий вид:

 

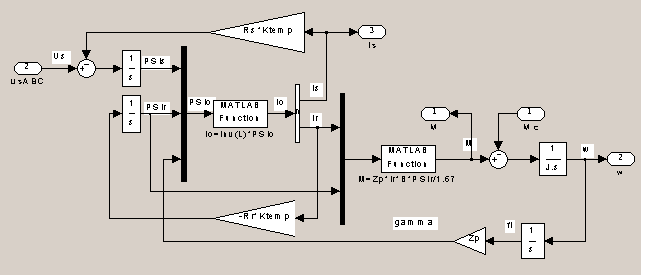
Рисунок  1 – Структурна схема моделювання АД у трифазній системі координат.

 

 

Програмна функція визначення матриці струмів:

 

function y = nivelir_matrix(u)

 

global Lm lsf lrf; a=u(7);

c1=cos(a); c2=cos(a+2*pi/3); c3=cos(a+4*pi/3);

 

M=[lsf  -1/2  -1/2  c1   c2   c3;

   -1/2  lsf  -1/2  c3   c1   c2;

   -1/2 -1/2   lsf  c2   c3   c1;

    c1   c3    c2   lrf -1/2 -1/2;

    c2   c1    c3  -1/2  lrf -1/2;

    c3   c2    c1  -1/2 -1/2 lrf];

M=2/3*Lm*M; psi=u(1:6); psi=psi(:);

y=M\psi;

 

 

 

Програмна функція визначення моменту:

 

function Mem=nivelir_moment(u)

global Zp Lm

u=u(:)';

D=[0 1 -1;-1 0 1;1 -1 0];

Ir=u(1:3);

PSIr=u(4:6)';

Mem=Zp*Ir*D*PSIr/sqrt(3);