Акименко Ирина Геннадьевна

Email: akimika@front.ru

Донецкий национальный технический университет
факультет: Вычислительной техники и информатики
cпециальность "Программное обеспечение автоматизированных систем"

  Тема диссертации "Система ввода и отображения графических данных для визуализации механических узлов в реальном времени"
Руководитель: проф., доктор технических наук Башков Евгений Александрович

Методы представления дискретных трехмерных данных

Этот текст является выдержкой из дипломной работы, защищенной на факультете ВМиК МГУ в 2002-м году. В статье проводится анализ и классификация методов представления и визуализации трехмерных моделей в приложении к задаче интерактивной визуализации сложных объектов реального мира.

1.1 Классификация моделей и методов визуализации

В настоящее время известно довольно большое число различных методов представления трехмерных объектов и связанных с ними методов визуализации, в том числе многомасштабных. Все представления можно разделить на несколько классов, обладающих характерными свойствами:

• Поверхностные / объемные;
• Связанные / дискретные;
• Явные / параметрические.

Поверхностные модели описывают только поверхность объекта в трехмерном пространстве. В противоположность им, объемные (воксельные) структуры позволяют задавать модели как часть трехмерного пространства, разбитого некоторым образом на ячейки, которые считаются заполненными, если они содержат часть объекта, и пустыми Ц в противном случае.

Связанные модели явно или неявно содержат информацию о непрерывных участках поверхностей моделей, тогда как дискретные представления описывают только приближение поверхности объекта.

Явное задание моделей предполагает, что описание модели объекта в данном представлении доступно в явной форме, а параметрическое Ц что для его получения необходимо дополнительно вычислять некоторую функцию, зависящую от параметра.

Методы визуализации можно условно разделить на проекционные методы и методы трассировки лучей.

Проекционные методы Ц это методы, в которых синтез изображения выполняется с помощью аффинных преобразований и преобразований проекции. Трехмерная сцена как набор примитивов визуализации (обычно, многоугольников, точек, линий и т.п.) трансформируется в двухмерный массив, который и отображается на экране монитора.

Методы трассировки лучей работают на уровне пикселей выходного изображения, рассчитывая их цвет на основе данных о геометрии сцены и положения виртуальной камеры.

Сегодня интерактивную скорость синтеза изображений предоставляют только проекционные методы, часто при поддержке аппаратного обеспечения. В дальнейшем в работе рассматриваются только такие методы, что в свою очередь накладывает некоторые ограничения на возможные представления объектов. Характерной особенностью поставленной задачи является работа с реальными данным, т.е. данными, введенными в компьютер с помощью устройств дистанционного сканирования. Такие данные в большинстве случаев дискретны и заданы явно, обычно в виде набора точек или набора карт глубины. Кроме того, за исключением томографов (этот случай в работе не рассматривается), получающих внутреннюю структуру объекта, все сканеры работают только с поверхностью объекта. Таким образом, представление должно хорошо описывать явно заданные дискретные поверхности.

Проведем анализ различных представлений с целью выявления пригодности их использования для решения поставленной задачи. В тексте не рассматриваются различные параметрические и процедурные представления, так как их особенности (сложность вычислений, отсутствие аппаратной поддержки) делает затруднительным использование этих представлений для моделирования реальных объектов.

1.2 Полигональные сетки

Полигональные сетки являются на данный момент самым распространенным представлением, для которого создано большое количество программного обеспечения, позволяющего редактировать, передавать по сети и визуализировать модели с использованием аппаратной поддержки.

Характерной особенностью полигональных сеток является поддержка связности модели. В силу этого полигональные представления хорошо применимы для описания большого числа синтетических поверхностей.

Однако, отсканированные данные, изначально не содержат информации о связности и непрерывности поверхностей, а представляют собой набор близко расположенных частиц (sample). Такие ограничения следуют из устройства сканирующего механизма, который обладает дискретным шагом конечного разрешения.

Следовательно, для использования полигональных моделей связность должна быть введена искусственно на этапе препроцессирования. Таким образом, полигональные модели не предназначены для прямой работы с отсканированными данными, так как требуют восстановления поверхности, что в общем случае является нетривиальной задачей и сильно зависит от класса обрабатываемых объектов. При этом восстановленная поверхность не обязательно будет использоваться на этапе визуализации (например, если модель такой сложности, что проекция треугольника на экран при типичной проекции просмотра сравнима по площади с одним пикселем).

С другой стороны, создано большое количество методов, позволяющих достаточно эффективно преобразовывать дискретные отсканированные данные в полигональные сетки ([Curless 96], [Turk 94]). Более того, современное оборудование высокого класса позволяет выполнять преобразование в сетку аппаратно.

Гораздо сложнее обстоит ситуация с представлением больших объемов данных и поддержкой различных уровней детализации. Структура полигональных сеток линейна и они не обеспечивают «естественной» поддержки многомасштабности, поэтому работа с большими сетками затруднена и требет различных, зачастую вычислительно сложных методов упрощения. Было создано множество алгоритмов для создания многомасштабных представлений на основе сеток, имеющих непосредственное отношение к поставленной задаче.

Сэмплирующие алгоритмы упрощают первоначальную геометрию модели, используя либо подмножество исходных точек, либо пересечение вокселей с моделью на трехмерной сетке. Такие алгоритмы лучше всего работают на гладких поверхностях без острых углов.

Алгоритмы, использующие адаптивное разбиение находят простую базовую (base) сетку, которая затем рекурсивно разбивается для аппроксимации первоначальной модели. Такой подход работает хорошо, когда найти базовую модель относительно просто. Например, базовая модель для участка ландшафта обычно прямоугольник. Для достижения хороших результатов на произвольных моделях требуется создание базовой модели, отражающей важные свойства исходной, что может быть нетривиально.

Прореживающие алгоритмы итеративно удаляют вершины или грани из полигональной сетки, производя триангуляцию после каждого шага. Большинство из них используют только локальные изменения, что позволяет выполнять упрощение довольно быстро.

Схемы со слиянием вершин работают с помощью свертывания двух или более вершин детализированной модели в одну, которая в свою очередь может быть совмещена с другими вершинами. Слияние вершин треугольника уничтожает его, уменьшая общее число треугольников модели. Обычно алгоритмы используют сложные методы определения, какие вершины нужно слить вместе и в каком порядке. Методы, использующие слияние ребер (edge collapse), всегда сливают вершины, разделяющие одну грань. Такие методы сохраняют локальную топологию, и, кроме того, при некоторых условиях могут работать в реальном времени.

Сложность вычислений в этих методах высока и их использование не всегда оправдано при работе с дискретными данными, поскольку сложность появляется прежде всего из-за необходимости поддерживать связность модели (которая в нашем случае была искусственно введена на этапе препроцессирования). Другой причиной высокой сложности методов является линейная структура сетки, которую необходимо восстанавливать для визуализации с помощью графических API.

Обобщим свойства полигональных сеток в приложении к поставленной задаче

1.3 Воксельные модели

Классические воксельные (voxel) модели представляют собой трехмерный массив, каждому элементу которого сопоставлен цвет и коэффициент прозрачности. Такой массив задает приближение объекта с точностью, определяемой разрешением массива.

Воксельными (или объемными) методами визуализации называются методы визуализации трехмерных функций, в дискретном случае заданных, например, с помощью описанного выше массива.

Типичные методы воксельной визуализации обрабатывают массив, и формирует проекцию каждого его элемента на видовую плоскость ([Laur91], [Westover90]). Исходный массив представляет собой регулярную структуру данных, что существенно используется в методах визуализации. Обычно элемент массива визуализируется на экране в виде некоторого примитива, так называемого отпечатка (footprint) или сплата (splat). Различные методы отличаются способами вычислений формы и размеров сплата.

Так как объемы данных в воксельных представлениях значительны даже для небольших моделей, единственной реальной возможностью работать со сложными объектами является использование древовидных иерархий. В работе [Laur91] на основе исходного массива строится многомасштабное представление в виде восьмеричного дерева. Каждый узел дерева содержит усредненное значение цвета и прозрачности всех своих потомков. Кроме того, каждый узел дерева содержит переменную, показывающую среднюю ошибку, ассоциированную с данным узлом. Эта переменная показывает ошибку, возникающую при замене оригинального набора вокселей в данной области пространства на константную функцию, равную среднему значению цвета всех потомков данного узла. В дальнейшем это значение используется для управления качеством визуализации и уровнем деталей.

Несмотря на то, что воксельные методы ориентированы в первую очередь на научную визуализацию, многие идеи, использующиеся в этих методах, находят свое применение в других областях. Например, идея сплаттинга используется при работе с точечными представлениями, а также с представлениями, основанными на изображениях.

Обобщим свойства воксельных представлений в приложении к поставленной задаче

1.4 Модели, основанные на изображениях

Моделирование и визуализация, основанные на изображениях (Image-Based Modeling and Rendering, далее IBMR) представляют собой альтернативные подход к решению задач синтеза изображения [Debevec 00].

Такие методы не используют промежуточные структуры данных, и синтезируют итоговую картинку, основываясь на исходных данных Ц как правило, изображениях или изображениях с глубиной. Более формально метод визуализации, основанный на изображениях, можно определить как алгоритм, определяющий, как по конечному набору исходных (reference) изображений сцены получить новое, результирующее (resulting) изображение для заданной точки наблюдения и заданных параметров виртуальной камеры.

Структуры данных, используемые для такого алгоритма визуализации, могут сильно отличаться, неизменным остается ориентация методов на непосредственную работу с исходными данными, что делает методы IBMR концептуально близкими к поставленной задаче.

1.4.1 Изображения с картами глубины

Одной из самых простых структур данных, используемых в IBMR являются наборы изображений с картами глубины. Определим пару изображение + карта глубины как цветное изображение, которому сопоставлено полутоновое изображение соответствующего размера, интенсивность в каждой точке которого соответствует расстоянию от камеры до поверхности объекта.

Примечательным свойством представления является то, что современные дистанционные сканеры позволяют напрямую получать данные в виде карт глубины, а наиболее дорогие модели получают и цветовую информацию об объекте. Следовательно, такое представление максимально подходит для работы со сложными реальными данными, а задача состоит в разработке метода визуализации.

Следует заметить, что пара изображение + карта глубины однозначно определяет дискретное приближение поверхности в трехмерном пространстве, при этом качество приближения зависит от разрешения изображения и выбранного положения камеры.

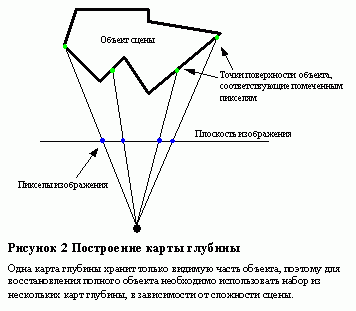
Одна карта глубины хранит только видимую часть объекта, поэтому для восстановления полного объекта необходимо использовать набор из нескольких карт глубины, в зависимости от сложности сцены.

Было предложено достаточно много методов визуализации и использования подобных структур данных. Например, Леонардо МакМиллан [McMillan 97] использует систему обработки изображений для деформации (warping) исходного изображения с учетом исходной и результирующей (текущей) камер таким образом, чтобы результат, визуализированный на экране, создавал иллюзию трехмерности. В работе Мартина Оливейры [Oliveira 00] также используется деформация изображений, однако результатом работы алгоритма являются текстуры созданные из карт глубины для текущего положения виртуальной камеры и наложенные на простую (плоскую) полигональную сетку Ц так называемые рельефные текстуры (relief textures).

Однако эти методы имеют серьезные недостатки. С одной стороны, в условиях недостаточной точности исходных данных и/или большом отклонении виртуальной камеры от исходной, в результирующем изображении возможно появление дырок (holes), т.е. ухудшения качества визуализации. С другой стороны, результатом работы дистанционных сканеров часто являются наборы данных из 50-70 карт глубины, которые в описанных выше алгоритмах будут обрабатывается сепаратно, создавая дополнительные погрешности визуализации. Кроме того, время визуализации одной карты глубины размером 512x512 по методу Оливейры на компьютере с процессором Pentium III 866 и видеокартой NVidia GeForce2 Pro составляет около 70 мс. Обработка 50-ти изображений займет около 4-х секунд, что недопустимо много для интерактивной работы с моделью.

Другим возможным вариантом является прямое восстановление трехмерных координат сэмплов (sample) и их визуализация напрямую с помощью проекции на видовую плоскость виртуальной камеры. Такой подход позволяет использовать аппаратное ускорение, так как пиксели исходных изображений в пространстве могут быть представлены точками или многоугольниками. Однако, на практике такой метод работает только для достаточно небольших наборов данных. Например, современная видеокарта со средним ускорителем бюджетного класса способна визуализировать около двух миллионов примитивов в секунду. В среднем карта глубины размером 512x512 содержит около 200 000 пикселей, принадлежащих модели, каждому из которых после восстановления положения в трехмерном пространстве будет соответствовать, как минимум, один примитив. Следовательно, при таких условиях на визуализацию 50-ти карт потребуется, как нетрудно подсчитать, около пяти секунд, что опять-таки не позволяет использовать этот метод для интерактивной визуализации.

Главным препятствием для создания многомасштабных методов визуализации карт глубины является отсутствие четкой пространственной структуры пары изображение + карта глубины. Таким образом, использование широко распространенных многомасштабных методов работы с изображениями в данному случае значительно затруднено.

1.4.2 Многослойные изображения с глубиной

В последнее время было предпринято несколько попыток использования многомасштабных методов вместе с основанными на изображениях представлениями.

Одна из них описана в работе Чанга и Бишопа [Chang 99] и в качестве базового представления использует многослойные изображений с глубиной (Layered Depth Images Ц LDI), впервые описанные в [Gortler 97].

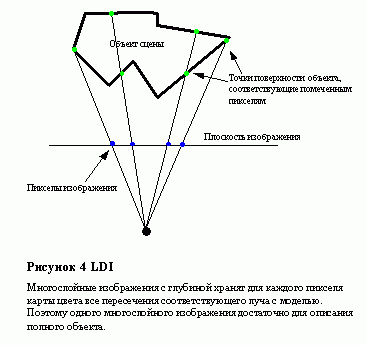
Многослойные изображения с глубиной хранят для каждого пикселя карты цвета все пересечения соответствующего луча с моделью. Поэтому одного многослойного изображения достаточно для описания полного объекта.

Отличие многослойных изображений с глубиной от простых заключается в том, что одно изображение позволяет хранить информацию не только о видимой с данной исходной камеры части поверхности объекта, а полную информацию об объекте. В сущности, LDI Ц это трехмерная структура данных, представляющая собой прямоугольную матрицу, каждым элементом которой является список точек. Каждая точка содержит глубину (расстояние до опорной плоскости) и атрибуты, в простейшем случае Ц цвет. Для представления всего объекта можно использовать единственное многослойное изображение, однако в [Bishop99] предложен способ, использующий шесть перспективных LDI с единым центром проекции.

Такая структура позволяет проводить визуализацию как описанными выше методами МакМиллана и Оливейры, так и просто использовать хранимую информацию как облако точек и визуализировать его напрямую с помощью одного из графических API (например, OpenGL).

С использованием LDI-подобных структур связаны некоторые ограничения на визуализацию, обусловленные тем, что все точки в изображении ориентированы на одну базовую плоскость. Кроме того, LDI не могу быть напрямую получены с устройств ввода и для создания такой структуры необходимо использование дополнительных алгоритмов, например, деформируя изображения с глубиной по методу МакМиллана таким образом, чтобы плоскость результирующего изображения совпадала с базовой плоскостью LDI. Отметим, что процесс формирования LDI происходит до непосредственной визуализации, и поэтому его эффективность ни отражается на скорости визуализации.

Однако LDI не позволяет напрямую визуализировать объект с различными степенями детализации. В работе [Chang99] была предпринята попытка создать многомасштабное представление на основе LDI с использованием так называемого дерева LDI (LDI tree).

Сущность метода состоит в следующем: вместо одного LDI формируется восьмеричное дерево, в каждом узле которого находится свой LDI и ссылки на другие узлы, в которых находится LDI меньшего размера (в единицах сцены), но того же разрешения. Также для каждого узла есть ограничивающий параллелепипед.

Все LDI в дереве имеют одинаковое разрешение. Высота дерева зависит от разрешения LDI. Чем меньше разрешение LDI, тем больше высота дерева. Каждый LDI в дереве содержит информацию только о той части сцены, которая содержится в его ограничивающем параллелепипеде. Ограничивающие параллелепипеды узлов следующего уровня дерева получаются дроблением ограничивающего параллелепипеда текущего уровня на восемь равных частей

Дерево LDI позволяет решать проблему визуализации очень больших структур данных, используя следующую идею: при визуализации нет необходимости обрабатывать потомков узла, если сам узел обеспечивает достаточную степень детализации. Авторы используют следующий критерий степени детализации: считается, что LDI обеспечивает достаточный уровень детализации, если "отпечаток" (footprint, splat) его пиксела на результирующем изображении покрывает не более одного пиксела экрана.

С другой стороны, использование того же подхода позволяет дополнить данные низкого разрешения искусственно восстановленными дополнительными уровнями дерева, создавая эффект фильтрации получаемого изображения.

Визуализация производится с помощью обхода дерева от корня к листьям и рисования LDI методом МакМиллана. При этом обработка всех узлов дерева не требуется, и обход ветви дерева завершается на первом LDI, обеспечивающем достаточную точность.

Алгоритм имеет высокое качество визуализации, возможность прогрессивной передачи данных. Однако его эффективность, как по времени, так и по памяти, достаточно низкая. Время получения изображения в разрешении 512?512 для LDI средней сложности на графической станции SGI Onyx2 (16Гбайт оперативной памяти, 32 процессора MIPS R1000 250Mhz) заняло более трех секунд. При этом потребовалось около 250Мбайт оперативной памяти.

Обобщим свойства основанных на изображениях представлений в приложении к поставленной задаче.

1.5 Точечные представления

Классические представления, основанные на изображениях, направлены на использование изображений в качестве примитивов визуализации. Повышение эффективности визуализации достигается за счет того, что время визуализации в них пропорционально не сложности геометрии, как в традиционных системах, основанных на полигональных сетках, а числу пикселей в исходных изображениях. Хотя такие подходы довольно хорошо работают для визуализации сложных объектов, они, как правило, требует значительных объемов памяти, визуализация страдает от появления артефактов в результирующем изображении, а также от невозможности работы с динамическим освещением. Кроме того, на сегодня не разработано эффективных многомасштабных алгоритмов.

Класс точечных (point sample) алгоритмов и представлений ([Levoy85], [Grossman98]) компенсируют недостатки IBМR при частичном сохранении описанных выше преимуществ.

Объекты моделируется как плотный набор точек поверхности, которые восстанавливаются из исходных изображений и сохраняются вместе с цветом, глубиной и информацией о нормали, делая возможным использование Z-буфера для удаления невидимых поверхностей, затенение по Фонгу, и другие эффекты, например, тени.

Метод визуализации таких данных напоминает классические методы деформаций (warping), но с тем различием, что (1) точки содержат дополнительную информацию о геометрии, и (2) они видонезависимы (view independent), т.е. цвет точки не зависит от направления, с которого она была восстановлена. Подобный подход использовался, например в [Max95] для реалистичной визуализации деревьев.

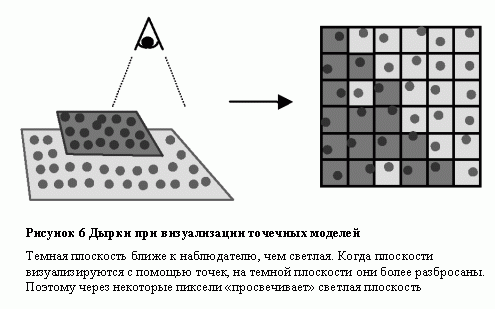
Основной проблемой визуализации моделей в таких представлениях является восстановление непрерывных поверхностей, т.е. гарантия отсутствия дырок после того, как положение каждой точки будет приведено к оконным координатам. Одним из возможных практических решений является сплаттинг (splatting), т.е. вычисление формы «отпечатка» точки на плоскости экрана. Такой подход используется, в частности, в [Levoy85]. Сплаттинг также часто используется в методах, основанных на изображениях. Возможны также другие подходы, например комбинация ресэмплинга и иерархического z-буфера ([Greene93]), недостатками которых является недостаточное использование современных аппаратных ускорителей, что выражается во времени визуализации около 3-5 секунд на кадр для не самых сложных сцен.

Главным недостатком точечных представлений, как и многих других, является сложность с представлением больших объемов данных. Использование неструктурированного набора точек позволяет достичь определенной гибкости при визуализации, но при увеличении объема на первый план выходят методы видозависимого упрощения, использовать которые в реальном времени не представляется возможным без введения дополнительных структур данных.

Обобщим свойства основанных на изображениях представлений в приложении к поставленной задаче.

1.6 Иерархические представления

Как правило, иерархические представления строятся на базе одного из представлений, рассмотренных выше. В подавляющем большинстве работ для построения иерархий используются древовидные структуры, например, восьмеричные деревья, или kd-деревья. Также используются общие виды трехмерных деревьев на основе иерархий описывающих сфер и кубов. Свойства иерархий могут сильно различаться в зависимости от базового представления, однако общие принципы построения и визуализации иерархических структур сходны между собой.

Нижний уровень дерева, т.е. совокупность листовых вершин, представляет собой максимально детализированную модель. Далее, поднимаясь к корню, атрибуты усредняются, структура упрощается до вырождения в один примитив на вершине дерева. Визуализация, наоборот, производится с помощью рекурсивного обхода дерева от вершины к листьям.

Иерархические структуры на базе полигональных сеток используются для динамического контроля за уровнем детализации и сложностью модели. В методе слияния вершин ([Xia97]) с узлом дерева ассоциирована вершина сетки, и переход к вышестоящему узлу дерева осуществляется с помощью слияния вершин. Воксельные иерархические модели используют восьмеричные деревья, так они наилучшим образом подходят для регулярной объемной структуры данных.

В работе [Levoy00-1] представлена система QSplat, использующая в качестве основы иерархии точечные сэмплы (sample). Точечные сэмплы Ц это точки, обладающие конечным размером и положением в пространстве, т.е. являющиеся аналогом неравномерно распределенных в пространстве вокселей. На их основе строится иерархия сфер, таких что, сфера, ассоциированная с внутренним узлом дерева, содержит множество своих потомков. Авторы использовали систему QSplat для визуализации очень сложных полигональных сеток, полученных в результате сканирования музейных статуй ([Levoy00-2]).

Обобщим свойства иерархических представлений в приложении к поставленной задаче.

1.7 Сравнение представлений и методов их визуализации

В таблице ниже приведено сравнение исследуемых методов в приложении к поставленной задаче. Как можно видеть, наилучшими характеристиками с точки зрения легкости получения данных с дистанционных сканеров, поддержки многомасштабности и аппаратной поддержки визуализации, обладают иерархические, точечные и основанные на изображениях представления. При этом изображения удобны с точки зрения получения данных. Точечные сэмплы показывают себя как удобный для дискретных представлений, хотя и не в полной мере универсальный примитив визуализации. А иерархические представления обладают естественной поддержкой многомасштабности, и, при должной организации, поддержкой прогрессивной передачи по сети.

Список литературы