Принципи синтезу зображення методом трасування променів.

1  Математичні моделі відбиття світла.

Розглянемо, як можна визначити колір пикселов зображення поверхні відповідно до інтенсивності відбитого світла при урахуванні взаємного розташування поверхні, джерела світла і спостерігача.

1.1  Дзеркальне відбиття світла.

Кут між нормаллю і падаючим променем () дорівнює куту між нормаллю і відбитим променем. Падаючий промінь, відбитий, і нормаль розташовуються в одній площині (рис. 1).

Поверхня вважається ідеально дзеркальною, якщо на ній відсутні будь-які нерівності, шорсткості. Власний колір у такої поверхні не спостерігається. Світлова енергія падаючого променя відбивається тільки по лінії відбитого променя. Яке-небудь розсіювання в сторони від цієї лінії відсутнє. У природі, імовірно, немає ідеально гладких поверхонь, тому вважають, що якщо глибина шорсткостей значно менше довжини хвилі випромінювання, то розсіювання не спостерігається. Для видимого спектра можна прийняти, що глибина шорсткостей істотно менше 0.5 мкм.

Якщо поверхня дзеркала відполірована неідеально, то спостерігається залежність інтенсивності відбитого світла від довжини хвилі - чим більше довжина хвилі, тим краще відбиття. Наприклад, червоні промені відбиваються сильніше, ніж сині.

При наявності шорсткостей мається залежність інтенсивності відбитого світла від кута падіння. Відбиття світла максимально для кутів , близьких до 90 градусів.

Падаючий промінь, потрапляючи на злегка шорсткувату поверхню реального дзеркала, породжує не один відбитий промінь, а кілька променів, що розсіюються по різних напрямках. Зона розсіювання залежить від якості полірування і може бути описана деяким законом розподілу. Як правило, форма зони розсіювання симетрична щодо лінії ідеального дзеркально відбитого променя. До числа найпростіших, але досить часто використовуваних, відноситься емпірична модель розподілу Фонга, відповідно до якої інтенсивність дзеркально відбитого випромінювання пропорційний , де  - кут відхилення від лінії ідеально відбитого променя. Показник  знаходиться в діапазоні від 1 до 200 і залежить від якості полірування. Запишемо це в такий спосіб:

,

де  - інтенсивність випромінювання джерела,  - коефіцієнт пропорційності.

1.2  Дифузійне відбиття.

Цей вид відбиття властивий  матовим поверхням. Матовою можна вважати таку поверхню, розмір шорсткостей якої вже настільки великий, що пажающий промінь розсіюється рівномірно в усі сторони. Такий тип відбиття характерний, наприклад, для гіпсу, піску, папера. Дифузійне відбиття описується законом Ламберта, відповідно до якого інтенсивність відбитого світла пропорційна косинусу кута між напрямком на точкове джерело світла і нормаллю до поверхні.

,

де  - інтенсивність джерела світла,  - коефіцієнт, що враховує властивості матеріалу поверхні. Значення  знаходиться в діапазоні від 0 до 1. Інтенсивність відбитого світла не залежить від розташування спостерігача.

Матова поверхня має свій колір. Колір матової поверхні, визначається комбінацією власного кольору поверхні і кольори випромінювання джерела світла.

При створенні реалістичних зображень варто враховувати те, що в природі, імовірно, не існує ідеально дзеркальних чи цілком матових поверхонь. При зображенні об'єктів засобами комп'ютерної графіки звичайно моделюють сполучення дзеркальності і дифузійного розсіювання в пропорції, характерної для конкретного матеріалу. У цьому випадку модель відбиття записують у виді суми дифузійного і дзеркального компонентів:

,

де константи ,  визначають відбивні властивості матеріалу.

Відповідно до цієї формули інтенсивність відбитого світла дорівнює нулю для деяких кутів  і . Однак у реальних сценах звичайно немає цілком затемнених об'єктів, варто враховувати фонове підсвічування, висвітлення розсіяним світло, відбитим від інших об'єктів. У такому випадку інтенсивність може бути емпірично виражена наступною формулою:

,

де - інтенсивність розсіяного світла,  - константа.

Можна ще вдосконалити модель відбиття, якщо врахувати те, що енергія від точкового джерела світла зменшується пропорційно квадрату відстані. Використання такого правила викликає складності, тому практиці часто реалізують модель, що виражається емпіричною формулою:

,

де  - відстань від центра проекції до поверхні,  - константа.

Як визначити колір зафарбовування точок об'єктів відповідно до даної моделі? Найбільше просто виконується розрахунок у градаціях сірого кольору (наприклад, для білого джерела світла і сірих об'єктів). У даному випадку інтенсивність відбитого світла відповідає яскравості. Складніше обстоїть справа з кольоровими джерелами світла, що висвітлюють кольорові поверхні Наприклад, для моделі RGB складаються три формули розрахунку інтенсивності відбитого світла для різних колірних компонентів. Коефіцієнти  та  різні для різних компонентів - вони виражають власний колір поверхні. Оскільки колір відбитого дзеркального променя дорівнює кольору джерела, то коефіцієнт , буде однаковим для всіх компонентів колірної моделі. Колір джерела світла виражається значеннями інтенсивності  для відповідних компонентів кольору.

1.3 Метод Гуро.

Цей метод призначений для створення ілюзії гладкої криволінійної поверхні, описаної у виді чи то багатогранників, чи полігональної сітки з пласкими гранями. Якщо кожна плоска грань має один постійний колір, визначений з урахуванням відбиття, то різні кольори сусідніх граней дуже помітні, і поверхня виглядає саме як багатогранник. Здавалося б, цей дефект можна замаскувати за рахунок збільшення кількості граней при апроксимації поверхні. Але зір людини має здатність підкреслювати перепади яскравості на границях суміжних граней - такий ефект називається ефектом смуг Маху. Тому для створення ілюзії гладкості потрібно набагато збільшити кількість граней, що приводить до істотного уповільнення візуалізації - чим більше граней, тим менше швидкість малювання об'єктів.

Метод Гуро ґрунтується на ідеї зафарбовування кожної плоскої грані не одним кольором, а плавно змінюються відтінками, що обчислюються шляхом інтерполяції кольору граней, що примикають. Зафарбовування граней по методу Гуро здійснюється в чотири етапи.

1. Обчислюються нормалі до кожної грані.

2. Визначаються нормалі у вершинах. Нормаль у вершині визначається усередненням нормалей граней, що примикають.

3. На основі нормалей у вершинах обчислюються значення интенсивностей у вершинах відповідно до обраної моделі відбиття світла.

4. Зафарбовуються полігони граней кольором, що відповідає лінійної інтерполяції значень інтенсивності у вершинах.

Вектор нормалі у вершині (a) дорівнює

.

Визначення інтерпольованих значень інтенсивності відбитого світла в кожній точці грані (і, отже, колір кожного пиксела) зручно виконувати під час циклу заповнення полігона. Розглянемо заповнення контуру грані горизонталями в екранних координатах.

Інтерпольована інтенсивність I у точці (X,Y) визначається виходячи з пропорції .

Звідси .

Значення интенсивностей I₁ і I₂ на кінцях горизонтального відрізка являють собою інтерполяцію інтенсивності у вершинах.

,

чи

,

.

 

1.4 Метод Фонга.

Аналогічний методу Гуро, але при використанні методу Фонга для визначення кольору в кожній точці інтерполюються не інтенсивності відбитого світла, а вектори нормалей.

1. Визначаються нормалі до граней.

2. По нормалях до граней визначаються нормалі у вершинах. У кожній точці зафарбовуваної грані визначається інтерпольований вектор нормалі.

3. По напрямку векторів нормалі визначається колір точок грані відповідно до обраної моделі відбиття світла.

Розглянемо, як можна одержати вектор нормалі в кожній точці грані. Для інтерполяції будемо оперувати векторами ,  і , що виходять з центра координат площини проектування і рівнобіжними відповідним нормалям N_a, N_b, і N_c у вершинах a, b і c (мал. 3.5).

Спочатку знайдемо  і :

,

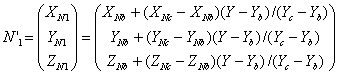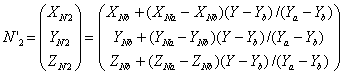
де - X_Na, Y_Na, Z_Na, X_Nb, Y_Nb, Z_Nb, X_Nc, Y_Nc, Z_Nc, координати векторів ,  і . Тепер знайдемо координати вектора N':

.

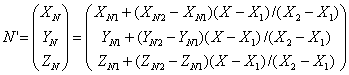Вектор N' є паралельним вектору N для нормалі в точці (X, Y), тому ми можемо використати його для розрахунку відбиття світла, як і вектор нормалі N.

Метод Фонга є набагато більш складним, ніж метод Гуро. Для кожного піксела поверхні необхідно виконувати набагато більше обчислень. Але він дозволяє отримати набагато кращий результат, особливо при імітації дзеркальних поверхонь.

2 Переломлення світла.

Закони переломлення світла варто враховувати при побудові зображень прозорих об'єктів.

2.1 Математична модель ідеального переломлення.

Відповідно до цієї моделі промінь відхиляється на границі двох середовищ, причому падаючий промінь, переломлений промінь і нормаль лежать в одній площині (у цій же площині лежить і дзеркально відбитий промінь). Позначимо кут між падаючим променем і нормаллю як , а кут між нормаллю і переломленим променем як . Для цих кутів відомий закон Снелліуса, відповідно до якого:

де n₁ і n₂ - абсолютні показники переломлення відповідних середовищ. На рис. 2 зображений приклад відхилення променя при переломленні. У даному випадку границями розділа середовищ є дві рівнобіжні площини, наприклад, при проходженні променя через товсте скло. Очевидно, що кут  дорівнює куту , а кут  дорівнює куту . Іншими словами, після проходження крізь скло промінь паралельно зміщується. Цей зсув залежить від товщини скла і співвідношення показників переломлення середовищ.

Окрім ідеального переломлення в комп'ютерній графіці (хоча і значно рідше, унаслідок складності реалізації) використовується дифузійне переломлення. Відповідно до цієї моделі падаючий промінь переломлюється в усі сторони. Прикладом може служити молочне скло.

3  Алгоритм трасування променів.

Методи трасування променів на сьогоднішній день вважаються найбільш  універсальними методами створення реалістичних зображень. Відомо багато прикладів реалізації алгоритмів трасування для якісного відбиття самих складних тривимірних сцен. Можна відзначити, що універсальність методів трасування в значній мірі обумовлена тим, що в їхній основі лежать прості і ясні поняття, що відбивають наш досвід сприйняття навколишнього світу.

Як ми бачимо навколишню нас реальність? По-перше, потрібно визначитися з тим, що ми взагалі здатні бачити. Навколишні нас об'єкти володіють стосовно світла такими властивостями:

 - випромінюють;

 - відбивають і поглинають;

 - пропускають крізь себе.

Кожну з цих властивостей можна описати деяким набором характеристик. Наприклад, випромінювання можна охарактеризувати інтенсивністю, спрямованістю, спектром. Випромінювання може виходити від умовно точкового джерела (далека зірка) чи протяжного. Поширення випромінювання може відбуватися уздовж досить вузького променя (промінь лазера), конусом (прожектор), рівномірно в усі сторони (Сонце), або ще як-небудь. Властивість відбиття (поглинання) можна описати характеристиками дифузійного розсіювання і дзеркального відбиття. Прозорість можна описати ослабленням інтенсивності і переломленням.

Той самий об'єкт реальної дійсності може вважатия джерелом світла, а при іншому розгляді може розглядатися як предмет, який тільки відбиває чи пропускає світло.

3.1  Метод прямого трасування променів.

Розглянемо, як формується зображення якої-небудь сцени, яка містить у собі декілька просторових об’єктів. Будемо вважати, що з точок поверхні (об’єму) випромінюючих об’єктів виходять промені світла. Такі промені можна назвати первісними – вони освітлюють все інше. Важливим моментом є припущення, що промінь світла у вільному просторі розповсюджується вздовж прямої лінії. Але в геометричній оптиці вважають, що промінь світла поширюється прямолінійно доти, поки не зустрінеться поверхня, що відбиває, чи границя середовища переломлення..

Від джерел випромінювання виходить по різних напрямках незліченна безліч первинних променів (навіть промінь лазера неможливо ідеально сфокусувати - усе рівно світло буде поширюватися не однією ідеально тонкою лінією, а конусом, пучком променів). Деякі промені ідуть у вільний простір, а деякі попадають на інші об'єкти. Якщо промінь попадає в прозорий об'єкт, то, переломлюючись, він йде далі, при цьому деяка частина світлової енергії поглинається. Подібно цьому, якщо на шляху променя зустрічається дзеркально відбиває поверхня, то він таюке змінює напрямок, а частина світлової енергії поглинається. Якщо об'єкт дзеркальний і одночасно прозорий (наприклад, звичайне скло), то буде вже два промені- у цьому випадку говорять, що промінь розщеплюється.

Можна сказати, що в результаті дії на об’єкти первинних променів виникають вторинні промені. Незліченна безліч вторинних променів іде у вільний простір, але деякі з них попадають на інші об'єкти. Так, багаторазово відбиваючись і переломлюючись, окремі світлові промені приходять у точку спостереження – око людини чи оптичну систему камери. Очевидно, що в точку спостереження може потрапити і частина первинних променів безпосередньо від джерел випромінювання. Таким чином, зображення сцени формується деякою безліччю світлових променів.

Колір окремих точок зображення визначається спектром і інтенсивністю первинних променів джерел випромінювання, а також поглинанням світлової енергії в об'єктах, що зустрілися на шляху відповідних променів.

Безпосередня реалізація даної променевої моделі формування зображення представляється скрутною. Можна спробувати побудувати алгоритм побудови зображення зазначеним способом. У такому алгоритмі необхідно передбачити перебір усіх первинних променів і визначити ті з них, що попадають в об'єкти й у камеру. Потім виконати перебір усіх вторинних променів, і також врахувати тільки ті, котрі попадають в об'єкти й в камеру і далі. Можна назвати такий метод прямим трасуванням променів. Практична цінність такого методу викликає сумнів. Справді, якщо буде нескінченна безліч променів, що йдуть в усі сторони? Очевидно, що повний перебір нескінченного числа променів у принципі неможливий. Навіть якщо якимось образом звести це до кінцевого числа операцій (наприклад, поділити всю сферу напрямків на кутові сектори й оперувати вже не звичайно тонкими лініями, а секторами), усе рівно залишається головний недолік методу- багато зайвих операцій, зв'язаних з розрахунком променів, які потім не використовуються. Так, у всякому разі, це представляється у дійсний час.

3.2  Метод зворотнього трасування.

Дозволяє значно зменшити перегляд світлових променів. Згідно з цим методом, трасування променів виконується не від джерел світла, я в зворотньому напрямку – від точки спостерігача. Так ми враховуємо тільки ті промені, які впливають на формування зображення.

Розглянемо, як можна отримати растрове зображення якої-небудь тривимірної сцени методом зворотнього трасування. Припустимо, що площина проекції розбита на велику кількість квадратиків – пікселів. Оберемо центральну проекцію з центром на деякій відстані від від площини проекції. Проведемо пряму лінію з центра через піксел на площині проекції. Це буде первісний промінь зворотнього трасування. Якщо пряма лінія цього променя потрапляє в один чи декілька об’єктів сцени, обираємо найближчу точку пересічення. Для отримання кольору піксела зображення потрібно враховувати якості об’єкта, а також те, яке світлове випромінювання буде у відповідній точці об’єкту.

Якщо об'єкт дзеркальний (хоча б частково), тоді будуємо вторинний промінь - промінь падіння, вважаючи променем відбиття попередній, первинний промінь. Вище ми розглядали дзеркальне відбиття й одержали формули для вектора відбитого променя по заданих векторах нормалі і променя падіння. Але тут нам відомий вектор відбитого променя, а як знайти вектор падаючого променя? Для цього можна використовувати ту ж саму формулу дзеркального відбиття, але визначаючи необхідний вектор променя падіння як відбитий промінь. Тобто відбиття навпаки.

Для ідеального дзеркала досить потім простежити лише чергову точку перетинання вторинного променя з деяким об'єктом. Що означає термін "ідеальне дзеркало"? Будемо думати, що в такого дзеркала ідеально рівна відполірована поверхня, тому одному відбитому променю відповідає тільки один падаючий промінь. Дзеркало може бути затемненим, тобто поглинати частина світлової енергії, але все рівно залишається правило: один промінь падає- один відбивається. Можна розглядати також "неідеальне дзеркало". Це буде означати, що поверхня нерівна. Напрямку відбитого променя буде відповідати кілька падаючих променів (чи навпаки, один падаючий промінь породжує кілька відбитих променів), що утворять деякий конус, можливо, несиметричний, з віссю уздовж лінії падаючого променя ідеального дзеркала. Конус відповідає деякому закону розподілу интенсивностей, найпростіший з який описується моделлю Фонга - косинус кута, зведений у деякий ступінь. Неідеальне дзеркало різке ускладнює трасування- потрібно простежити не один, а безліч падаючих променів, враховувати внесок випромінювання від інших видимих з даної точки об'єктів.

Якщо об'єкт прозорий, те необхідно побудувати новий промінь, такий, котрий при переломленні давав би попередній трассируемый промінь. Тут також можна скористатися оборотністю, що справедлива і для переломлення. Для розрахунку вектора шуканого променя можна застосувати розглянуті вище формули для вектора променя переломлення, вважаючи, що переломлення відбувається в зворотному напрямку.

Якщо об'єкт має властивості дифузійного відбиття і переломлення, то, у загальному випадку, як і для неідеального дзеркала, необхідно трасувати промені, що приходять від усіх наявних об'єктів. Для дифузійного відбиття інтенсивність відбитого світла, як відомо, пропорційна косинусу кута між вектором променя від джерела світла і нормаллю. Тут джерелом світла може виступати будь-який видимий з даної точки об'єкт, здатний передавати світлову енергію.

Коли з'ясовується, що поточний промінь зворотного трасування не перетинає будь-який об'єкт, а йде у вільний простір, то на цьому трасування цього променя закінчується.

Зворотне трасування променів у тім виді, у якому його тут розглянуто хоч і скорочує перебір, але не дозволяє позбутися від нескінченного числа аналізованих променів. Справді, даний метод дозволяє відразу одержати для кожної точки зображення єдиний первинний промінь зворотного трасування. Однак вторинних променів відбиття вже може бути нескінченна кількість.

При практичній реалізації методу зворотного трасування вводять обмеження. Деякі з них необхідні, щоб можна було в принципі вирішити задачу синтезу зображення, а деякі обмеження дозволяють значно підвищити швидкодію трасування. Розглянемо приклади таких обмежень.

1. Серед усіх типів об'єктів виділимо деякі, котрі назвемо джерелами світла. Джерела світла можуть тільки випромінювати світло, але не можуть, його відбивати чи переломлювати. Будемо розглядати тільки точкові джерела світла.

2. Властивості поверхонь, що відбивають, описуються сумою двох компонент - дифузійної і дзеркальної.

3. У свою чергу, дзеркальність також описується двома складовими. Перша (reflection - відбиття) враховує відбиття від інших об'єктів, що не є джерелами світла. Будується тільки один дзеркально відбитий промінь r для подальшого трасування. Другий компонент (specular - відблиск) означає світлові відблиски від джерел світла. Для цього направляються промені на всі джерела світла і визначаються кути, утворені цими променями з дзеркально відбитим променем зворотного трасування (r). При дзеркальному відбитті колір точки поверхні визначається кольором того, що відбивається. У найпростішому випадку дзеркало не має власного кольору поверхні

4. При дифузійному відбитті враховуються тільки промені від джерел світла. Промені від дзеркально відбивають поверхонь ігноруються. Якщо промінь, спрямований на дане джерело світла, закривається іншим об'єктом, виходить, дана точка об'єкта знаходиться в тіні. При дифузійному відбитті колір освітленої точки поверхні визначається власним кольором поверхні і кольором джерел світла.

5 Для прозорих (transparent) об'єктів звичайно не враховується залежність коефіцієнта переломлення від довжини хвилі. Іноді прозорість узагалі моделюють без переломлення, тобто напрямок переломленого променя t збігається з напрямком падаючого променя.

6. Для обліку освітленості об'єктів світлом, що розсіюється іншими об'єктами, уводиться фонова складова (ambient).

7. Для завершення трасування вводять деяке граничне значення освітленості, що уже не повинне вносити вклад у результуючий колір, або обмежують кількість ітерацій.

Відповідно до моделі Уіттеда колір деякої точки об'єкта визначається сумарною інтенсивністю:

,

де  - довжина хвилі, С() - заданий вхідний колір точки об'єкта, K_а, K_d, K_s, K_r і K_t,- коефіцієнти, що враховують властивості конкретного об'єкта параметрами фонового підсвічування, дифузійного розсіювання, зеркаль-яости, відбиття і прозорості,

I_а - інтенсивність фонового підсвічування,

I_d - інтенсивність, що враховується для дифузійного розсіювання,

I_s - інтенсивність, що враховується для дзеркальності,

I_r - інтенсивність випромінювання, що приходить по відбитому променю,

I_t - інтенсивність випромінювання, що приходить по переломленому променю.

Інтенсивність фонової підсвітки (I_а) для об’єкта за звичай є постійною. Запишемо формули для інших інтенсивностей. Для дифузійного відбиття:

,

де  - інтенсивність i-го джерела світла,  - кут між нормаллю до поверхні об’єкту і напрямком на це джерело світла.

Для дзеркальності:

де p – покажчик ступеня від одиниці до кількох сотень (згідно моделі Фонга),  - кут між відбитим променем і напрямком на i-те джерело світла.

Інтенсивності випромінювань, які проходять по відбитому променю (I_r), а також по переломленому променю (I_t), помножують на коефіціент, який враховує послаблення інтенсивності від відстані, яку пройшов промінь. Такий коефіціент має вид , де d – відстань, що пройдена, а  - параметр ослаблення, який враховує якості середовища, у якому розповсюджується промінь.

Якщо об'єктів досить багато, то об'єкти (чи оболонки) можна поєднувати в групи - для декількох об'єктів одна оболонка. Таким чином, вибудовується вже ієрархія оболонок: на нижньому рівні оболонки для одиночних об'єктів, на наступному рівні - оболонки оболонок і так далі Така деревоподібна структура може мати кілька рівнів. Це дозволяє істотно прискорити процес перебору, зробити час роботи пропорційним (теоретично) логарифму числа об'єктів.

А тепер зробимо загальні висновки по методу зворотного трасування променів.

Позитивні риси:

1. Універсальність методу, його застосовність для синтезу зображень досить складних просторових схем. Втілює багато законів геометричної оптики. Просто реалізуються різноманітні проекції.

2. Навіть усічені варіанти даного методу дозволяють одержати досить реалістичні зображення. Наприклад, якщо обмежитися тільки первинними променями (із точки проектування), те це дає видалення невидимих точок. Трасування вже двох-одного-двох вторинних променів дає тіні, дзеркальність, прозорість.

3. Усі перетворення координат (якщо такі є) лінійні, тому просто працювати з текстурами.

4. Для одного пиксела растрового зображення можна трасувати трохи близько розташованих променів, а потім усреднять їхній колір для усунення ефекту ступінчастості (антиаліасінг).

5. Оскільки розрахунок окремої точки зображення виконується незалежно від інших точок, те це може бути ефективно використане при реалізації даного методу в рівнобіжних обчислювальних системах, у яких промені можуть трассироваться одночасно.

Недоліки:

1. Проблеми з моделюванням дифузійного відбиття і переломлення.

2. Для кожної точки изображеня необхідно виконувати багато обчислювальних операцій. Трасування променів відноситься до числа самих повільних алгоритмів синтезу зображень.