|
Рис.1 Архитектура САПР |
Верхняя часть рисунка 1 - модель традиционной архитектуры САПР, нижняя часть-модель СПРУТ-технологии. Ядро в традиционной архитектуре представляет собой универсальное средство, которое тиражируется на рынке в качестве программного продукта. Однако для того, чтобы конкретный специалист на рабочем месте мог эффективнорешать свои задачи, на базе геометрического моделлера необходимо разработать специализированное приложение. На каждом предприятии должно быть множество таких приложений. Стоимость их создания с использованием универсальных алгоритмических языков типа С++ и привлечением квалифицированных программистов в десятки раз превышает стоимость геометрических моделлеров. В итоге многие отечественные фирмы затратив миллионы долларов на приобретение универсальных импортных систем испытывают острое неудовлетворенное от результатов. В мартовском номере журнала "Компьютер пресс" в статье "Как я пришел к СПРУТ-технологии" отмечалось, что для оп-тимизации соотношения эффективность/цена необходимо, чтобы каждое рабо-чее место располагало необходимым и достаточным набором программных средств. Традиционная архитектура САПР не удовлетворяет этому требованию, в связи с чем ряд ведущих зарубежных и отечественных фирм приступили к созданию систем новой архитектуры. Настоящая статья освещает решения предлагаемые СПРУТ-технологией(см. "Компьютер пресс" № 4’97) в части обработки геометрических знаний.
Геометрические модели, данные и знания
Под математической и в том числе геометрической моделью понимают определенное множество абстрактных объектов или несколько множеств абстрактных объектов разной природы, различающихся условно приписываемыми им именами, в совокупности с заданной системой отношений между элементами этих множеств. M = < A; R1s1,..., Rnsn > Здесь M - математическая модель, A - носитель модели, Risi- i-е отношение мо-дели ( i = 1,..., n). Носителем модели является основное конечное или счетное множество A={a1,..., am}, на котором определены отношения Rsi О Eisi. Множество {R1s1,..., Rnsn } называется сигнатурой модели. При si=2 имеем бинарные отношения (am, an) О R2, при si=3 тернарные (al, am, an)ОR3, при si=n N-арные (al, am, ...,an)ОRn . В геометрических моделях носителями являются геометрические объекты: точки, линии, поверхности, твердые тела. Сигнатура геометрической модели строится на базе унарных, бинарных и N-арных операций над геометрическими объектами: преобразования, пересечения, сложения, вычитания, объединения и т.п. Мощность геометрического моделлера определяется номенклатурой объектов и операций, которые могут быть использованы в нем. В соответствии с известной формулой:
программа = данные + алгоритмы
программные средства состоят из пассивной компоненты, подлежащей обработке (данные), и активной обрабатывающей компоненты (алгоритмы). В широком смысле алгоритмы представляют собой знания. Знания могут быть представлены в процедурной форме на алгоритмических языках либо в непроцедурной форме как базы знаний. Алгоритмические языки наиболее эффективны для представления математических и в том числе геометрических знаний. Однако, математические знания способны покрывать только отдельные острова или архипелаги в безбрежном море плохо формализуемых (экспертных) знаний. Экспертные знания представляются с помощью методов и средств искусственного интеллекта, к которым должны подключаться знания математические. Это символически изображено в виде модели СПРУТ-технологии на рис.1, где в отличие от традиционной архитектуры, приложения строятся не с помощью языков типа С++ или Паскаль, а на основе активных интеллектуальных объектов. Эти методы и средства предполагается описать в последующих статьях.
Средства хранения геометрических данных в СПРУТ-технологии
На рис.1 показано, что сердцевиной любой архитектуры является база данных. Геометрическая модель необходима для задания идеальной формы, которой должно было бы соответствовать изделие(рис.2), а модель физического тела - дать характеристику материала, из которого изготовляется изделие, и допустимые отклонения реальных изделий от идеальной формы.

|
Рис.2 Геометрическая модель самолета |
Результаты проектирования хранятся в базах данных.В связи со спецификой представления информации геометрические модели хранятся в геометрических базах данных, а негеометрические - в базах данных реляционного типа. При этом информация в обеих базах должна быть взаимосвязана. В связи с тем, что машиностроительные изделия представляют собой иерархическую систему объектов(сборочная единица, узел, деталь, элемент детали), в графической базе удобно использовать иерархическую модель данных. В СПРУТ-технологии графическая база содержит иерархию графических сегментов. Управление графическим данными осуществляется с помощью подсистемы DOG. Над графической базой данных можно выполнить следующие операции: создание новой базы(NEWBASE<имя базы>). открытие существующей базы(OLDBASE<имя базы>), просмотр текущей базы с выводом иерархической структуры и возможностью просмотра любого сегмента ее (LOOKBASE). Над сегментами графической базы выполняются следующие операции. Создание сегмента(MKSEGM<имя сегмента>). Подсегмент создается в текущем сегменте. Каждый из сегментов базы может иметь до 32-х подсегментов. Имя сегмента должно содержать путь к нему, например MKSEGM "\вид1\сеч2". Копирование сегмента(COPYSEGM<имя сегмента>). Оператор осуществляет копирование содержимого указанного сегмента в текущий сегмент. При задании дополнительной информации возможно копирование с преобразованиями (сдвигом-поворотом-масштабированием). Изменение сегмента(CGSEGM<имя сегмента>). Выполняется переход в существующий сегмент после чего новая информация будет пополнять его. Вывод сегмента(OUTSEGM{<имя сегмента>}). Вывод сегмента на текущее устройство графического вывода. Очистка сегмента(CLRSEGM{<имя сегмента>}). Просмотр сегмента(LOOKSEGM{<имя сегмента>}). Оператор осуществляет вывод содержимого указанного сегмента на экран. Выбор сегмента(SELSEGM{<имя сегмента>}). Интерактивный выбор сегмента из текущей базы. Имя выбранного сегмента присваивается строковой переменной, заданной в команде. Определение оболочки сегмента(SHELSEGM{<имя сегмента>},Pi,Pj). Выполняет расчет описанного прямоугольника со сторонами, параллельными осям. Pi - левая нижняя точка, Pj - правая верхняя точка. Удаление сегмента(DELSEGM<имя сегмента>). Операция удаления сегмента выполняется в базе активной на данный момент. Система обладает возможностями импорта и экспорта чертежей. Импортируется чертеж из файла типа DXF в новый сегмент текущей активной базы. Подсегмент с указанным именем будет создан в текущем выбранном в дереве базы сегменте. Имеются следующие возможности экспорта: DXF файл - экспорт чертежа в файл формата DXF; IGES файл - экспорт чертежа в файл формата IGES; плоттер 1 - вычерчивание чертежа на первом графопостроителе; плоттер 2 - вычерчивание чертежа на втором графопостроителе; принтер 1 - печать чертежа на первом принтере; принтер 2 - печать чертежа на втором принтере; файл плоттера 1 экспорт чертежа в файл в формате команд первого графопостроителя; файл плоттера 2 - экспорт чертежа в файл в формате команд второго графопостроителя; файл принтера 1- экспорт чертежа в файл в формате команд принтера; файл принтера 2 - экспорт чертежа в файл в формате команд принтера. Имеется возможность построения тексто-графических баз данных посредством оператора установления связи сегмента графической базы данных с таблицей реляционной базы. При этом ссылка на таблицу реляционной базы хранится в сегменте базы графической.
Геометрические объекты СПРУТ-технологии
В табл.1 приведена классификация базовых геометрических объектов. По размерности параметрических моделей, необходимых для представления геометрических объектов, они делятся на нульмерные, одномерные, двухмерные и трехмерные. Нульмерные и одномерные классы геометрических объектов могут моделироваться как в двух координатах(2D) на плоскости, так и в трех координатах(3D) в пространстве. Двухмерные и трехмерные объекты могут моделироваться только в пространстве. Табл.1 содержит примеры операторов подсистем среды СПРУТ для моделирования обширной номенклатуры геометрических объектов. Эти примеры не исчерпывают всего богатства языка, который находится в состоянии постоянного развития. В языке СПРУТ приняты следующие обозначения: Xx, Yy, Zz ѕ декартовы координаты с их величинами; Rr, Aa, Mm ѕ радиусы, углы и расстояния с их величинами; Nn ѕ порядковый номер; Pi, Li, Ci, Ki ѕ точки, прямые, окружности и контуры с их номерами-индексами; CONIC i ѕ кривые второго порядка с их номерами-индексами; P3D i, L3D i, CC i ѕ пространственные точки, прямые и кривые с их номерами-индексами; Pl i, PlS i ѕ плоскости и плоскости с системой координат с их номерами-индексами; CYL i, CN i, HSP i, TOR i ѕ цилиндры, конусы, полусферы и торы с их номерами-индексами SS i, AS i ѕ технологические и аналитические поверхности с их номерами-индексами; SOLID(dsn) ѕ твердые тела с их номерами-индексами. Одним из важнейших геометрических объектов является контур. Контуры - последовательность сегментов плоских геометрических элементов, начинающихся и заканчивающихся точками, лежащими на первом и последнем элементе соответственно.
|
Таблица 1. Геометрические объекты в среде СПРУТ |
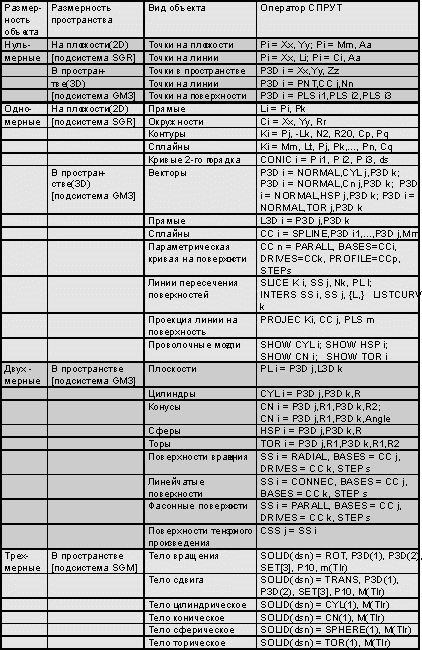
Геометрические операции в СПРУТ-технологии
В табл.2 приведена классификация геометрических операций и представление их в языке СПРУТ. Унарные операции выполняются над одним геометрическим объектом. В их число входят преобразования, проекции и расчеты параметров. Приведенный в табл.2 пример оператора масштабирования контура Kj представляет собой операцию гомотетии из Pk точки с коэффициентом пропорциональности Mm. Остальные операции преобразований производятся с помощью описанных в табл.2 матриц, которые применяются к соответствующим объектам. Оператор SURFAREA применительно к пространственной кривой CC i дает ее длину, применительно к контуру Ki ѕ площадь ограниченной им плоскости, а для ограниченной поверхности SS i и твердого тела SOLID i ѕ площадь соответствующей поверхности. Оператор с этим же именем позволяет рассчитать моменты инерции области, ограниченной контуром, относительно координатных осей и относительно прямой из этого контура. Имеется возможность расчета моментов инерции твердого тела относительно пространственной прямой и точки в пространстве. Центры масс могут быть определены для плоской области, ограниченной контуром, и для твердого тела. Бинарные операции позволяют рассчитывать расстояния и углы между двумя объектами; пересечения двух линий, линии с поверхностью, двух поверхностей и двух тел. С помощью операций вычитания и сложения можно из двух тел создать новое. Имеется возможность отсечения плоскостью части тела, а также объединения двух поверхностей с приоритетом по Z. Операция объединения может быть произведена над несколькими поверхностями.
|
Таблица 2 Геометрические операции в среде СПРУТ |
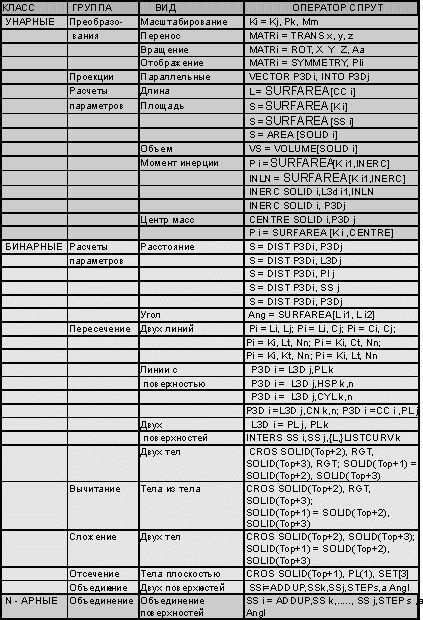
Система геометрического моделирования в СПРУТ-технологии
На рис.3 представлена система геометрического моделирования среды СПРУТ. Эта система реализована в трех подсистемах SIGI, GM3, SGM и представляет собой множество описанных выше геометрических объектов и связей между ними. Интерактивное моделирование на плоскости производится с помощью системы SIGI. Система GM3 обеспечивает моделирование в пространстве точек линий и поверхностей, а интерактивная система SGM предназначена для моделирования твердых тел и расчета их массо-инерционных характеристик. Основная цель моделирования на плоскости - формирование контуров. Контур представляет собой последовательность отрезков прямых, дуг окружностей и сплайнов. При построении контуров могут быть использованы многогранники и спирали Архимеда. Точки используются для задания начала и конца контура и в качестве опорных точек пересечения соседних элементов. Контуры, построенные в SIGI применяются для формирования плоских пространственных кривых в GM3 и образования с их помощью контуры кинематических поверхностей. Эти же используются при построении в SGM тел вращения и сдвига (математических цилиндров) .
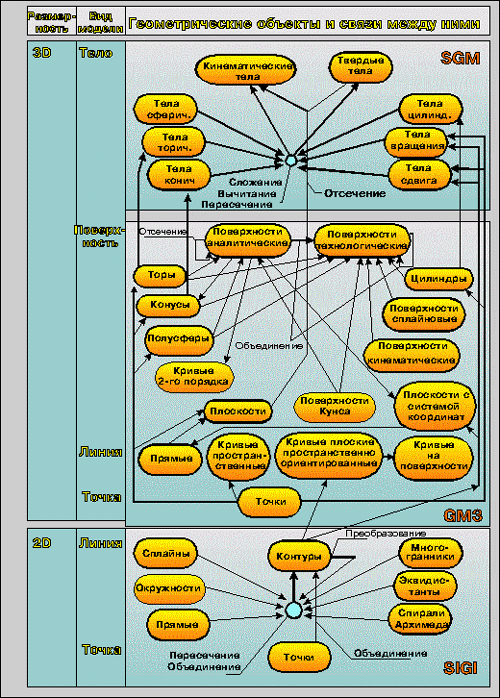
|
Рис. 3 Геометрическое моделирование в среде СПРУТ |
Основная цель моделирования в пространстве в системе GM3 - построение аналитических и технологических поверхностей. Аналитические поверхности необходимы для построения модели формы детали, а технологические для расчета траектории фрезерной обработки поверхностей. Технологические поверхности представляются в виде каркаса траекторий точки касания инструмента при их обработке. Твердые тела в системе SGM образуются из простых тел - цилиндра, конуса, сферы, тора, тел вращения и сдвига - с помощью операций сложения, вычитания, пересечения, а также отсечения плоскостью.
