8.2. Перемножение матриц
Рассмотренный в предыдущем подразделе пример представляет наиболее простой для распараллеливания тип задач, в которых в процессе выполнения подзадач не требуется выполнять обмен информацией между процессорами. Такая ситуация имеет место всегда, когда переменная распараллеливаемого цикла не индексирует какие-либо массивы (типичный случай - параметрические задачи). В задачах линейной алгебры, в которых вычисления связаны с обработкой массивов, часто возникают ситуации, когда необходимые для вычисления матричные элементы отсутствуют на обрабатывающем процессоре. Тогда процесс вычисления не может быть продолжен до тех пор, пока они не будут переданы в память нуждающегося в них процессора. В качестве простейшего примера задач этого типа рассмотрим задачу перемножения матриц.
Для обсуждения проблемы приведем сначала однопроцессорный вариант программы:
PROGRAM MATMULT
IMPLICIT NONE
INTEGER I,J,K,N,NM
PARAMETER ( NM=2000)
REAL*8 A(NM,NM),B(NM,NM),C(NM,NM)
REAL*8 TIME
WRITE(*,*) СInput NТ
READ(*,*) N
C начальная инициализация массивов
DO 1 I = 1,N
DO 1 J = 1,N
A(I,J) = DBLE(I)
B(I,J) = 1./DBLE(J)
1 CONTINUE
WRITE(*,*) 'N = ',N
C включаем таймер
TIME = SECOND()
C блок вычисления
DO 2 I = 1,N
DO 2 J = 1,N
C(I,J) = 0.0
DO 3 K = 1,N
3 C(I,J) = C(I,J) + A(I,K)*B(K,J)
2 CONTINUE
C фиксируем время выполнения программы и печатаем контрольную
C информацию (угловые матричные элементы результирующей матрицы
C С(1,1) = C(N,N) = N, С(1,N)= 1, C(N,1)= N*N)
TIME = SECOND() - TIME
WRITE(*,10) C(1,1),C(1,N),C(N,1),C(N,N)
10 FORMAT(2X,2F16.6)
WRITE(*,*) ' TIME CALCULATION: ', TIME
END
Следует отметить, что представленный вариант программы неэффективно работает на современных вычислительных системах. Простая модификация блока вычислений с введением промежуточного массива для хранения строки матрицы А значительно увеличивает скорость работы программы (на компьютерах Pentium III примерно в 2 раза, а на Alpha DS20E в 10 раз!):
DO 1 I = 1,N
DO L = 1,N
ROW(L) = A(I,L)
END DO
DO 1 J = 1,N
C(I,J) = 0.0D0
DO 3 K = 1,N
3 C(I,J) = C(I,J) + ROW(K)*B(K,J)
1 CONTINUE
Это объясняется более эффективным использованием быстродействующей кэш-памяти. В языке программирования ФОРТРАН двумерные массивы располагаются в памяти компьютера по столбцам, поэтому выборка элементов из массива А выполняется из далеко расположенных друг от друга ячеек памяти. Вынесение этой операции из самых внутренних циклов значительно ускоряет работу программы. В языке С аналогичную процедуру следует применить к массиву В.
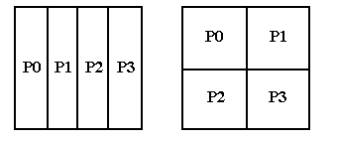
Получение максимальной производительности на многопроцессорных системах представляет собой значительно более сложную задачу. Существует множество вариантов решения этой задачи на многопроцессорных системах. Алгоритм решения существенным образом зависит от того, производится или нет распределение матриц по процессорам, и какая топология процессоров при этом используется. Как правило, задачи такого типа решаются либо на одномерной, либо на двумерной сетке процессоров. На Рис. 20 представлено распределение матрицы в памяти 4-х процессоров, образующих одномерную и двумерную сетки.
Рис. 20. Пример распределения матрицы на одномерную и двумерную сетки процессоров.
Первый вариант значительно проще в использовании, поскольку позволяет работать с заданным по умолчанию коммуникатором. В случае двумерной сетки потребуется описать создаваемую топологию и коммуникаторы для каждого направления сетки. Каждая из трех матриц (A,B и С) может быть распределена одним из 4-х способов:
Отсюда возникает 64 возможных вариантов решения этой задачи. Большинство из этих вариантов плохо отражают специфику алгоритма, и, соответственно, заведомо неэффективны. Тот или иной способ распределения матриц однозначно определяет, какие из трех циклов вычислительного блока должны быть подвержены процедуре редукции. Ниже предлагается вариант программы решения этой задачи, который в достаточно полной мере учитывает специфику алгоритма. Поскольку для вычисления каждого матричного элемента матрицы С необходимо выполнить скалярное произведение строки матрицы А на столбец матрицы В, то матрица А разложена на одномерную сетку процессоров по строкам, а матрица В - по столбцам. Матрица С разложена по строкам, как матрица А (Рис. 21).
Рис. 21. Пример распределения матриц на 4 процессора.
При таком распределении строка, необходимая для вычисления некоторого матричного элемента, гарантированно находится в данном процессоре, а столбец хотя и может отсутствовать, но целиком расположен в некотором процессоре. Поэтому алгоритм решения задачи должен предусматривать определение, в каком процессоре находится нужный столбец матрицы B, и пересылку его в тот процессор, который в нем нуждается в данный момент. На самом деле, каждый столбец матрицы B участвует в вычислении всего столбца матрицы С, и поэтому его следует рассылать во все процессоры.
PROGRAM PMATMULT
INCLUDE 'mpif.h'
C параметры:
С NM - полная размерность матриц;
С NPMIN - минимальное число процессоров для решения задачи;
С NPS - размерность локальной части матриц
PARAMETER (NM = 500, NPMIN=4, NPS=NM/NPMIN+1)
REAL*8 A(NPS,NM), B(NM,NPS), C(NPS,NM), COL(NM)
REAL*8 TIME
С в массивах NB и NS информация о декомпозиции матриц:
С NB - число строк матрицы в каждом процессоре;
С NS - номер строки, начиная с которой хранится матрица в данном
С процессоре;
С предполагается, что процессоров не больше 64.
INTEGER NB(0:63), NS(0:63)
С инициализация MPI
CALL MPI_INIT(IERR)
CALL MPI_COMM_RANK(MPI_COMM_WORLD, IAM, IERR)
CALL MPI_COMM_SIZE(MPI_COMM_WORLD, NPROCS, IERR)
IF(IAM.EQ.0) WRITE(*,*) 'NM = ',NM,' NPROCS = ',NPROCS
C вычисление параметров декомпозиции матриц
С алгоритм реализует максимально равномерное распределение
NB1 = NM/NPROCS
NB2 = MOD(NM,NPROCS)
DO I = 0,NPROCS-1
NB(I) = NB1
END DO
DO I = 0,NB2-1
NB(I)= NB(I)+1
END DO
NS(0)=0
DO I = 1,NPROCS-1
NS(I)= NS(I-1) + NB(I-1)
END DO
C заполнение матрицы А, значения матричных элементов определяются
С глобальным индексом строки. Здесь IAM - номер процессора
DO J = 1,NM
DO I = 1,NB(IAM)
A(I,J) = DBLE(I+NS(IAM))
END DO
END DO
С заполнение матрицы В
DO I = 1,NM
DO J = 1,NB(IAM)
B(I,J) =1./DBLE(J+NS(IAM))
END DO
END DO
C включение таймера
TIME = MPI_WTIME()
С Блок вычисления,
С циклы по строкам и по столбцам переставлены местами и цикл по
С столбцам разбит на две части: по процессорам J1 и по элементам
С внутри процессора J2. Это сделано для того, чтобы не вычислять,
С в каком процессоре находится данный столбец. Переменная J выполняет
С сквозную нумерацию столбцов.
С цикл по столбцам
J = 0
DO J1 = 0,NPROCS-1
DO J2 = 1,NB(J1)
J = J + 1
С процессор, хранящий очередной столбец, рассылает его всем остальным
С процессорам
IF(IAM.EQ.J1) THEN
DO N = 1,NM
COL(N) = B(N,J2)
END DO
END IF
CALL MPI_BCAST(COL, NM, MPI_DOUBLE_PRECISION, J1,
*MPI_COMM_WORLD,IERR)
С цикл по строкам (именно он укорочен)
DO I = 1,NB(IAM)
C(I,J) = 0.0
С внутренний цикл
DO K = 1,NM
C(I,J) = C(I,J) + A(I,K)*COL(K)
END DO
END DO
END DO
END DO
TIME = MPI_WTIME() - TIME
С печать контрольных матричных элементов из тех процессоров, где
С они хранятся
IF(IAM.EQ.0) WRITE(*,*) IAM,C(1,1),C(1,NM)
IF(IAM.EQ.NPROCS-1)
*WRITE(*,*) IAM, C(NB(NPROCS-1),1), C(NB(NPROCS-1), NM)
IF(IAM.EQ.0) WRITE(*,*) ' TIME CALCULATION: ', TIME
CALL MPI_FINALIZE(IERR)
END
В отличие от программы вычисления числа , в этой программе практически невозможно выделить изменения по сравнению с однопроцессорным вариантом. По сути дела - это совершенно новая программа, имеющая очень мало общего с прототипом. Распараллеливание в данной программе заключается в том, что каждый процессор вычисляет свой блок матрицы С, который составляет приблизительно 1/NPROCS часть полной матрицы. Нетрудно заметить, что пересылки данных не потребовались бы, если бы матрица В не распределялась по процессорам, а целиком хранилась в каждом процессоре. В некоторых случаях такая асимметрия в распределении матриц бывает очень выгодна.