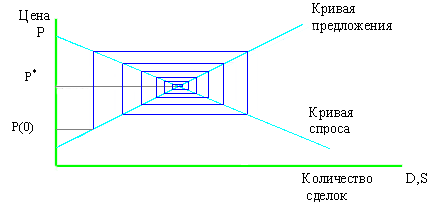
Изобразим процесс рыночного регулирования графически в виде модели, которую обычно называют паутинообразной (cobweb model).
Задача
Будем считать, что на рынке одного товара функция спроса D(t)
и функция предложения S(t) - линейные функции цены P(t) на момент времени
t или цены P(t-1) предыдущего момента времени.
Функция спроса:
D(t) = a + A*P(t),
где a,A - постоянные параметры.
Функция предложения:
S(t) = b + B*P(t),
где b,B - постоянные параметры.
Суть паутинообразной модели заключена в следующем:
а) Предложение реагирует на цены с некоторым лагом (отставанием во времени);
иными словами, сегодняшнее предложение S(t) определяется ценой предыдущего периода P(t-1),
а сегодняшний спрос D(t) определяется ценой текущего периода P(t).
б) Цены каждого периода P(t) устанавливаются на таком уровне, чтобы уравнять спрос
и предложение, т. е. на уровне, при котором D(t)=S(t).
Приведенные положения определяют порядок вычислений:
Цены предшествующего периода ® Текущее предложение ®
Текущий спрос и существующие цены ® Предложение следующего периода ® и
т. д.
Поскольку кривая спроса направлена слева направо и сверху вниз (при A<0), а кривая предложения слева направо и снизу вверх (при B>0), рыночная цена, которая в процессе регуляции стремится достичь величины равновесия P* , движется попеременно то вверх, то вниз, вычерчивая соответствующую этому циклу ломаную.

Программа Micro4:
1. Изображает кривую спроса D=a + A*P и кривую предложения S=b + B*P на плоскости, по оси абцисс которой отложена цена P, а по оси ординат - количество сделок.
2. Вычисляет начальное предложение S(1) исходя из начального значения цены P(0) на момент времени T = 0.
3. Изображает маршрут "изменение цены ® изменение числа сделок", который имеет вид "паутины", повторив несколько раз процессы (i) и (ii):
(i) определение P(t) таким образом, чтобы S(t) = S(P(t-1)) = D(t) = D(P(t));
(ii) нахождение s(t+1) = SP(t)), соответствующего P(t), T=1,2,...,TT.