www.mi.ru/~dupliksv/pauk/glava4.html
Принципы построение обучающих систем
1. Структура обучающей системы
Итак, создание обучающих систем на базе ЭВМ - это один из перспективных способов повышения эффективности процесса обучения.
Объектом управления при обучении является обучаемый. Субъектами управления выступают преподаватель и обучающая система (т.к. она не заменяет, а дополняет преподавателя).
Целью обучения, т.е. целью работы обучаемого с обучающей системой является получение:
Цель и результат деятельности обучаемого образуют учебную деятельность [14]. Учебная деятельность организуется не субъектом деятельности (обучаемым), а объектом (преподавателем). Для того, чтобы цель и результат совпадали, необходимо управление учебной деятельностью. Результат учебной деятельности является свойством самого субъекта.
Исходя из этого, учебная программа должна включать в себя 3 основные части [7,13]:
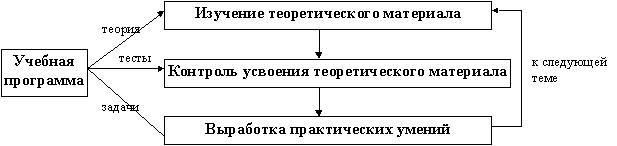
а процесс обучения можно представить схемой (рис. 3.1.1
):
Рис. 3.1.1. Схема процесса обучения
Обучающие системы можно классифицировать на две группы [16]:
В селективных обучающих системах управление обучением (определение формы, содержания, последовательности информационных кадров, тестов, задач, помощи и т.д.) осуществляется автором системы. При этом каждый обучаемый проходит один и тот же путь обучения, то есть нет адаптации к каждому конкретному обучаемому. Достоинство таких систем - универсальность, то есть предметная независимость. Недостаток - низкая адаптивность.
Схематично такую обучающую систему можно представить на рис. 3.1.2.
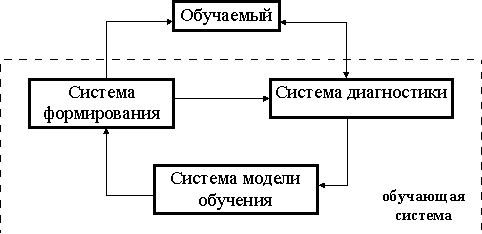
Рис. 3.1.2. Структура селективной обучающей системы
Рассмотрим кратко назначение всех систем.
Система формирования задания
. Предназначена для генерации задач в соответствии со степенью обученности обучаемого. Представляет из себя совокупность базы данных с заданиями и подпрограммы, формирующей или выбирающей задание из базы. Сгенерированное задание поступает обучаемому и на систему диагностики.Система диагностики
. Предназначена для контроля знаний обучаемого. Она осуществляет ввод ответа, сравнивает его с правильным ответом и принимает решение о правильности выполнения задания.Система модели обучения
. Предназначена для формирования последовательности обучения. Принимает информацию о результатах обучения и принимает решение о продолжении обучения.В интеллектуальных обучающих системах
управление обучением определяется самой обучающей системой на основании результатов обучения. Здесь сценарий обучения формируется динамически в соответствии с текущей ситуацией. Реализация осуществляется на основании знаний о предметной области, о процессе обучения, об обучаемом. Недостатком является предметная ориентация, то есть привязка к конкретной предметной области.Схематично такую обучающую систему можно представить на рис. 3.1.3.
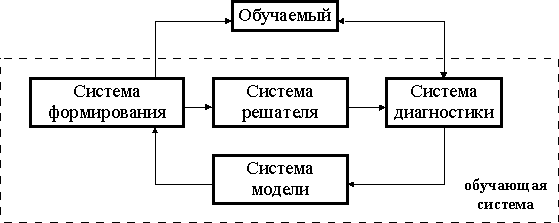
Рис. 3.1.3. Структура интеллектуальной обучающей системы
Здесь добавлена еще одна система - решатель проблем. Его назначение - решение сгенерированного задания. Наличие данной системы позволяет отказаться от предварительного формирования заданий и эталонных ответов к ним. Однако, создание подобного решателя, пригодного для любой области знаний, невозможно.
Одной из основных функций учебной программы является управление познавательной деятельностью обучаемого. Для этого программа должна получать сведения о ходе процесса обучения, об усвоении обучаемым учебного материала, о результатах тестирования и выполнения практических заданий. То есть в системе “учебная программа - обучаемый” должна присутствовать обратная связь
[6].Обратная связь может быть двух видов: внутренняя и внешняя.
Внутренняя обратная связь - это информация, которая поступает от обучающей программы к обучаемому в ответ на его действия при выполнении заданий. Она предназначена для самокоррекции обучаемым своей учебной деятельности и дает возможность обучаемому сделать осознанный вывод об успешности или ошибочности учебной деятельности. Она является стимулом к дальнейшим действиям, помогает оценить и скорректировать результаты учебной деятельности. Различают консультирующую и результативную внутреннюю обратную связь. Консультация может быть разной: помощь, разъяснение, подсказка, наталкивание и т.п. Результативная обратная связь также может быть различной: от "верно - неверно" до демонстрации правильного результата или способа действия.
Внешняя обратная связь - это информация, которая поступает от обучающей программы к преподавателю. С ее помощью он корректирует учебную деятельность обучаемого, а также может скорректировать сценарий обучения.
Схема взаимодействия с обратной связью представлена на рис. 3.1.4.
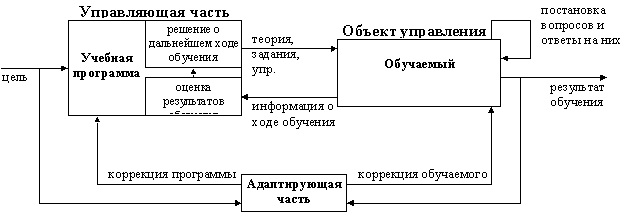
Рис. 3.1.4. Схема обучения в системе “учебная программа –
обучаемый” с обратной связью
Как видно из схемы, на обучающую программу поступает цель обучения. В соответствии с этой целью программа выдает обучаемому теоретический материал, примеры, задания, а также информацию, которая управляет ходом обучения (например, помощь при навигации по учебному материалу). Обучаемый изучает теорию, решает задачи, после чего результаты его деятельности поступают в программу (обратная связь).
Достаточно важным моментом в ходе познавательной деятельности обучаемого является его умственная деятельность, в ходе которой обучаемый сам формулирует вопросы, возникающие в ходе обучения, и сам отвечает на них.
Программа получает информацию о ходе обучения, анализирует ее, выставляет оценку обучаемому и принимает решение о дальнейшем ходе обучения.
В результате у обучаемого вырабатываются определенные знания, умения и навыки, которые будем называть результатом обучения
.Также в программу входит адаптирующая часть. Ее задача состоит в коррекции хода обучения, т.е. настройке его под конкретного обучаемого. Она получает информацию о цели и результате обучения, сравнивает их и корректирует работу обучающей программы и ход познавательной деятельности обучаемого.
Таким образом, можно сказать, что результат обучения есть функция от цели обучения и коррекции.
Если рассмотреть систему “преподаватель - учебная программа - обучаемый”, то схема обучения примет вид (рис. 3.1.5):

Рис. 3.1.5. Схема обучения в системе “преподаватель - учебная программа - обучаемый”
В этой схеме главное место занимает преподаватель. Он ставит цель обучения, получает информацию о ходе обучения и может вносить дополнительную коррекцию в работу программы и в ход познавательной деятельности обучаемого наравне с адаптирующей частью.
3.2. Целевые показатели учебного
процесса
Для того, чтобы количественно отразить дидактические показатели, вводятся целевые показатели обучения и изложения материала [2,11].
Все показатели делятся на две группы: количественные и качественные (рис. 3.2.1):
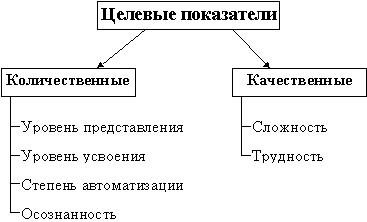
Рис. 3.2.1. Целевые показатели
Рассмотрим эти показатели.
1. Уровень представления учебного материала
Различают четыре формы представления учебного материала, соответствующие различным уровням абстракции в описании:
Уровень представления обозначается b и может меняться соответственно от 1 до 4.
2. Уровень усвоения учебного материала
Этот показатель характеризует качество владения обучаемым учебным материалом. Такая классификация позволяет четко формулировать дидактические цели при проектировании учебной программы и на их основе определять его состав.
Различают пять уровней усвоения учебного материала:
Уровень представления обозначается a и может меняться соответственно от 0 до 4.
Для измерения степени владения учебным материалом на каждом уровне используют коэффициент:
 ,
,
где
|
|
- |
количество правильно выполненных существенных операций в процессе тестирования |
|
|
- |
общее количество существенных операций в тесте. |
Исходя из этого: ![]()
Таким образом, уровень усвоения учебного материала может быть использован для оценивания качества знаний у обучаемого и выставления оценки. Предлагаются следующие критерии для оценок:
|
|
неудовлетворительно |
|
|
удовлетворительно |
|
|
хорошо |
|
|
отлично |
При ![]() следует
продолжать процесс обучения на том же уровне.
следует
продолжать процесс обучения на том же уровне.
Предлагается также следующая последовательность обучения с учетом уровня усвоения учебного материала (рис. 3.2.2).
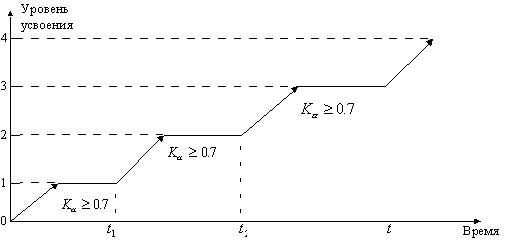
Рис. 3.2.2. Последовательность обучения с учетом уровня
усвоения учебного материала
В соответствии с этой схемой, процесс обучения должен происходить следующим образом. У обучаемого есть некоторые базовые знания на нулевом уровне усвоения, поэтому он сразу начинает обучение на первом уровне, либо сперва проходит предварительную проверку знаний и по ее результатам пропускается на первый уровень. Он изучает новый
учебный материал, после чего проводится проверка усвоения этого материала на первом уровне. Если обучаемый проходит эту проверку с коэффициентом
3. Степень автоматизации усвоения
Этот показатель характеризует умения как навыки в овладении осваиваемыми способами деятельности. Измеряется он с помощью коэффициента:
![]() ,
,
где:
|
|
- |
время выполнения теста профессионалом |
|
|
- |
время выполнения теста обучаемым |
4. Осознанность
Это умение обосновать выбор способа действия. Различают три степени осознанности:
Осознанность обозначается g и может меняться соответственно от 1 до 3.
5. Сложность
Это понятие относительное. Сложность зависит от уровня представления учебного материала (b ), количества операций, необходимого для достижения результата при решении задач. Принцип от простого к сложному означает движение в ходе обучения от низшего уровня b к высшему.
6. Трудность
Это понятие тоже относительное. Оно связано с уровнем усвоения учебного материала (a ) и зависит от обучаемого: от степени его предварительной подготовки, от его умственных способностей.
3.3. Модель освоения учебного материала
Модель освоения учебного материала показывает, в какой последовательности должны изучаться темы и каковы логические связи между ними [11].
На начальном этапе проектирования учебного курса планируемый для изучения учебный материал разбивают на отдельные учебные элементы.
В состав модели освоения входят матрицы отношений очередности и логических связей учебных элементов, последовательности изучения учебных элементов, граф логических связей учебных элементов (рис. 3.3.1). Построение модели производят в четыре этапа:
Матрицы отношений очередности и логических связей учебных элементов являются квадратными. Размер их равен количеству учебных элементов. Сначала строятся пустые матрицы и нумеруются их строки и столбцы в соответствии с возрастанием учебных элементов (см. рис. 3.3.1, а и б). Далее выполняется построчное заполнение ячеек матриц нулями и единицами.
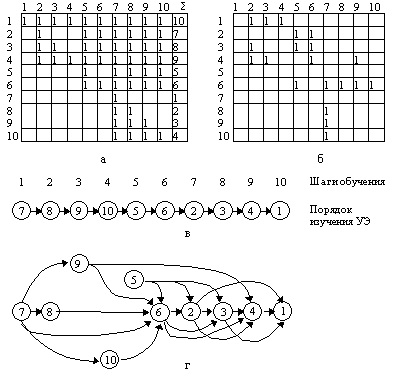
Рис. 3.3.1. Пример модели освоения учебного материала:
а - матрица отношений очередности учебных элементов
б - матрица логических связей учебных элементов
в - последовательность изучения учебных элементов
г - граф логических связей
При заполнении ячеек матрицы отношений очередности анализируют отношение очередности между двумя учебными элементами. Единицу ставят в ячейку, если учебный элемент, указанный в номере строки, должен изучаться после учебного элемента, указанного в номере столбца. Противоположное отношение очередности обозначают нулем или оставляют соответствующую ячейку матрицы пустой. Все ячейки главной диагонали матрицы отношений очередности заполняют единицами. Ячейки матрицы, симметричные относительно главной диагонали, должны иметь противоположные значения. Поэтому анализ
парных отношений очередности можно проводить лишь для левого нижнего или для правого верхнего треугольника матрицы, заполняя ее оставшуюся часть на основе свойства антисимметрии.При заполнении матрицы логических связей учебных элементов ставят единицу в ячейку, если учебный материал учебного элемента, указанного в номере строки, логически связан с учебным материалом учебного элемента, указанного в номере столбца. Составление матрицы логических связей удобно вести на основе матрицы отношений очередности путем исключения единиц из тех ячеек, для которых отсутствуют логические, опорные связи между элементами (см. рис. 3.3.1, а и б).
Процесс заполнения матриц целесообразно вести, имея перед глазами тексты с учебным материалом по всем учебным элементам. Анализ содержания учебного материала позволяет более объективно выявлять парные отношения очередности и логические связи между учебными элементами.
На вид матриц отношений очередности и логических связей, а, следовательно, и на форму представления учебного материала оказывают влияние не только объективные, но и субъективные факторы: вкусы разработчика, его привычки, интуитивные представления, склад мышления и т.д.
Последовательность изучения учебных элементов в пошаговой процедуре обучения определяют в процессе обработки матрицы отношений очередности, суммируя коэффициенты каждой строки матрицы. Полученные суммы записывают в колонке справа от матрицы (см. рис. 3.3.1, а). Величины сумм указывают порядковые номера соответствующих учебных элементов в списке последовательности изучения учебного материала (рис. 3.3.1, в).
Логические связи учебных элементов отображают для наглядности в виде ориентированного графа (рис. 3.3.1, г). Строят граф по матрице логических связей учебных элементов.
Ребра графа логических связей указывают на опорные связи между учебными элементами. Так, ребра, связывающие учебный элемент 2 с учебными элементами 5 и 6 (см. рис. 3.3.1, г), указывают, что для освоения содержания учебного материала из учебного элемента 2 необходимо сперва изучить материал учебных элементов 5 и 6.
Модель освоения учебного материала комплекса определяет последовательность его изложения в обучающей системе, варианты траекторий его изучения, логические связи при построении гипертекста.
В заключении приведем пример построения матриц отношений очередности учебных элементов, логических связей учебных элементов и графа логических связей на примере разработки учебного курса “Основы теории вероятности: события, алгебра событий, вероятность”.
Учебный материал разбивается на 10 тем:
Пусть темы изучаются в том порядке, в котором они перечислены. Тогда матрица отношений очередности примет вид (рис. 3.3.2):
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
3 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
3 |
|
4 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
4 |
|
5 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
5 |
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
6 |
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
7 |
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
8 |
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
9 |
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
10 |
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
11 |
Рис. 3.3.2. Матрица отношений очередности
Матрицу логических связей можно представить в двух видах: полном (рис. 3.3.3) и сокращенном (рис. 3.3.4).
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
4 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
5 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
6 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
7 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
8 |
1 |
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
9 |
1 |
1 |
1 |
1 |
|
1 |
|
1 |
|
|
|
|
10 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Рис. 3.3.3. Полная матрица логических связей
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
1 |
|
|
|
|
|
|
|
|
6 |
|
|
|
1 |
|
|
|
|
|
|
|
|
7 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
8 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
1 |
|
|
|
|
10 |
|
1 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
1 |
|
1 |
|
1 |
1 |
|
Рис. 3.3.4. Сокращенная матрица логических связей
Сокращенная матрица строится из полной исключением лишних связей. Например, для изучения 5-го учебного элемента (вероятность появления хотя бы одного события) обучаемый должен сперва изучить 4-й учебный элемент (теорема умножения вероятностей), 2-й учебный элемент (вероятность события) и 1-й учебный элемент (события, алгебра событий) (см. рис. 3.3.3). Но для изучения 4-го учебного элемента также требуется знание 2-го и 1-го учебных элементов. Поэтому из связей 5-го учебного элемента можно исключить прямую связь с 1-м и 2-м учебными элементами. Косвенно связь с ними сохраняется через 4-й учебный элемент (см
. рис. 3.3.4).Соответственно, можно построить полный и сокращенный графы логических связей. Здесь будет приведен только сокращенный граф (рис. 3.3.5).
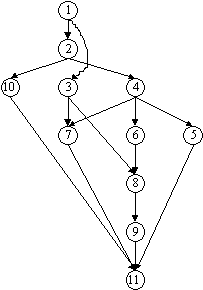
Рис. 3.3.5. Сокращенный граф логических связей
Полный граф логических связей строится аналогично по полной матрице логических связей.
| Оглавление | Дальше >> |