Источник: Несмеянов В.Ю., Мирный В.В. ДонГТУ,http://fgtu.donntu.ru/fm/1999-1/28.htm-электронная публикация.
УДК 622.225
Некоторые методы визуального представления горно-геологических данных при использовании современных технических средств
Кандидаты техн. наук. В.Ю.Несмеянов, В.В.Мирный (ДонГТУ
)Решение практически всех задач горного производства требует построения графической документации того или иного назначения. Это могут быть геологические разрезы, гипсометрические планы пластов, планы горных выработок, профили рельсовых путей, генеральный план строительства горного предприятия, рабочие чертежи проекта, схемы вентиляции, схемы электрохозяйства, чертежи конструкций отдельных узлов и т. п., вплоть до элементарных чертежей, представляющих эскиз для выполнения заказа ремонтными мастерскими. Во все времена существования добычных отраслей промышленности (как, впрочем, и всей деятельности человека) было стремление представлять информацию об объекте в форме изображения.
Получение графического изображения вручную зачастую являлось настолько трудоемкой, дорогостоящей и длительной процедурой, что потребителю часто приходилось просто от нее отказываться. Даже применение отдельных приспособлений и устройств, основанных на механических, оптических, электрических и других принципах не делали задачу получения изображения простой. Однако потребность в получении графического отображения информации столь высока, что это заставляло исследователей постоянно искать пути совершенствования получения изображений.
Необычайно широкие возможности открываются перед пользователями ЭВМ, память которой хранит или воспроизводит информацию в форме изображения. Диалог человека с машиной происходит вполне естественно и весьма эффективно. В зависимости от решаемой задачи изображение можно анализировать различными способами. Для получения общего представления об имеющемся объекте его рассматривают в целом, для получения более подробной информации его детализируют. Известно, что анализ текста требует от читателя глубоких знаний словаря и используемых правил грамматики. В то же время для понимания изображения не требуется никаких “особых” знаний. В конечном итоге цель любого изображения, каким бы оно ни было, состоит в предоставлении наблюдателю совокупности визуальных сведений, способствующих лучшему пониманию рассматриваемой сцены. Визуальные сведения подчиняются законам, определяющим явления визуального восприятия в окружающем нас реальном мире, то есть законам, в соответствии с которыми действуют механизмы анализа в мозгу человека [4]. Интерес к применению изображений объясняется их высокой информативностью. Это означает, что информация, содержащаяся в изображении, представлена в наиболее концентрированной форме, а ее восприятие не требует от получателя сверхзнаний.
С необходимостью графического отображения информации сталкивается почти каждый пользователь ПК. Чаще всего вывод графической информации осуществляется на цветной или монохромный экран дисплея. Другими устройствами вывода графической информации являются принтеры. Более сложными устройствами для вывода графической информации на бумагу являются графопостроители, перьевые и струйные плоттеры. При построении изображения объекта горно-геологического назначения пользователь стремится отобразить его характер с помощью точек, линий, поверхностей. Как известно, линия и поверхность является совокупностью точек. Можно считать, что любая поверхность может быть представлена как совокупность линий, или как “видимый” след линии, движущейся в пространстве, при этом сама линия может менять свою конфигурацию. Далее описана динамика простейшей визуализации информации при построении поверхности. Рассмотрим основные типы поверхностей [6].
Поверхность — линия, движущаяся в пространстве.
Линейный каркас поверхности — совокупность фиксированных положений взаимно перемещающихся линий образующих и направляющих. Если представить точки пересечения линий дискретно, образуется точечный каркас.
Графическая поверхность, образованная движением изменяющей свою форму образующей в соответствии с результатами расчетов, удовлетворяющим наложенным условиям (любой предмет дизайна).
Топографическая поверхность, образованная движением линии пересечения участков земной поверхности различного рельефа опускающейся или поднимающейся горизонтальной плоскостью.
Для описания формы, структуры, качественных особенностей месторождения используются поверхности топографического порядка, которые могут быть изображены в проекции на горизонтальную, вертикальную, любую наклонную плоскость [1].
В зависимости от типа решаемой задачи изолинии (в частном случае горизонтали) символически могут представить разнообразную информацию: топологическую, количественную, качественную, структурную и т.п. Для построения топографической поверхности обычно получают (например, в результате геологоразведочных работ) набор точек поверхности с определенными или вычисленными координатами
X, Y и Z. По этим координатам может быть получено достаточно детальное (отвечающее репрезентативности исходных данных) изображение поверхности, как результат сложных вычислений и громоздких построений. Но часто бывает, что для практических целей необходимо быстро оценить общий характер поверхности, не прибегая к детальным и сложным построениям (например, для определения необходимости доразведки залежи, оперативного получения запасов и т.п.).В любом случае природную поверхность необходимо
аппроксимировать. Под аппроксимацией понимают замену одних объектов
другими, более простыми, но близкими к исходным. В частности, поверхности
всех платоновых тел аппроксимируют поверхность сферы, но наиболее полно
это делает поверхность икосаэдра, состоящая из 20 равносторонних
треугольников. Замена кривой поверхности такой многогранной, у которой
гранями являются треугольники, называется триангуляцией. Возможности
достижения этой цели определяются особенностями структуры аппроксимируемой
поверхности. Всякая кривая поверхность имеет свой многогранный прототип,
является как бы пределом, к которому стремится вписанная в нее или
описанная вокруг нее многогранная поверхность при условии бесконечного
увеличения ее граней [5].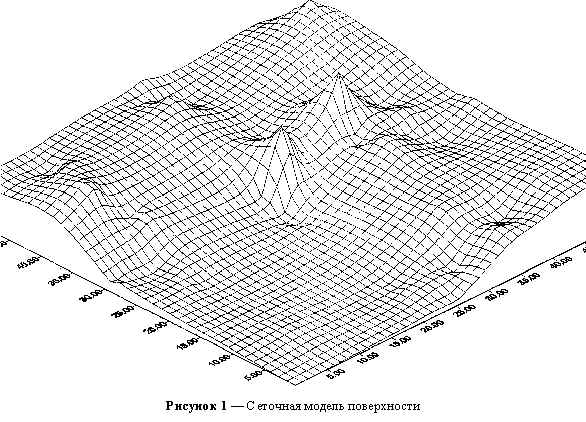
Замена естественной топографической поверхности более простой геометрической может быть выполнена построением какой-либо математической модели (полиномиальной, сплайновой, в виде рядов и т.д.). Наиболее простым и эффективным методом математического моделирования топографической поверхности является построение полиномиальной модели. Модель дает достаточную точность при аппроксимации простых участков поверхности со спокойным, выдержанным рельефом. При сложном рельефе, изменчивом характере простирания и падения залежи, полиномиальная модель может давать значительные погрешности. Получение высокоточной математической модели топографической поверхности описано в литературе и требует выполнения довольно громоздких вычислительных операций для каждой исходной точки: ограничения вокруг нее ближайшей окрестности с известными точками, построение матрицы нормальных уравнений и вектора коэффициентов, производства последовательных приближений на основе метода наименьших квадратов. Очевидно, что время построения модели зависит от количества точек, которых для получения большой точности требуется довольно много. Время вычислений зависит от времени выполнения элементарной операции. Подобными методами можно добиться очень хорошей точности модели, что, конечно, приветствуется, но не всегда, и, зачастую, не всегда имеется необходимость именно в высокой точности. Если нет необходимости в высокой точности, не решаются (в данный момент) какие-либо сложные технические задачи по топографической поверхности, а достаточно оценить только характер рельефа, может быть предложен более простой путь математического моделирования, что даст достаточную по точности информацию с несомненной экономией времени.
В качестве математической основы может быть взят метод двумерной интерполяции по формулам Ньютона и Лагранжа. Для получения модели в трехмерном пространстве разложим задачу на более простые, как описано ниже.
Мысленно разрежем изображаемую топографическую поверхность на слои, параллельные оси
X. При этом координаты Y точек не учитываются, они определяются положением слоя, а используются координаты Z точек. Таким образом, в слой параллельной оси X, попадает несколько известных точек, которые используются как узлы информации, а данные для недостающих точек могут быть вычислены по простым формулам. Полученные в слое точки можно мысленно соединить, что дает некоторую как бы направляющую в пространстве, изгибающуюся только в вертикальной плоскости. Для описания поверхности может быть получено достаточное количество таких направляющих. После этого в поперечных по отношению к направляющим направлениях через небольшие промежутки укладываем гибкие ленты — образующие, которые (при достаточно большом их количестве) образуют совместно с направляющими гибкую сеть с мелкими ячейками, которая повторяет собой форму моделируемой поверхности (рисунок 1). Пересечение направляющих и образующих образуют узлы сети отметки, которых можно вычислить. Если отметка узла окажется кратной некоторому интервалу, например высоте сечения изолинии или горизонталей, то этот узел отображается. При достаточно густой сети (частоту можно легко регулировать выбирая величину шага для построения направляющих и образующих) изображенных узлов будет достаточно для аппроксимации исходной топографической поверхности. В описанных условиях может быть решена и задача выбора оптимальной величины шага. Естественно, все это может быть выполнено не вручную, а с применение достаточно мощных ЭВМ, с соответствующими внешними устройствами для получения графических изображений.Рассмотрим математический аппарат двумерной интерполяции. Самым, пожалуй, простым методом интерполяции является двумерная интерполяция по формулам Ньютона и Лагранжа.
Линейная интерполяция — наиболее простой случай интерполяции, определение промежуточной величины лишь по двум данным значениям.
Если для
x0 и x0 + h функция принимает значение y0 =f (x0) и y1= f (x0+h), то для некоторого промежуточного значения аргумента x в интервале x0 и x0+h искомая величина определяется по приближенной интерполяционной формуле [2]:y = f (x) = y0+((x–x0)/h)*dy, dy = y1–y0 (1)
В общем случае интерполяционная формула сопоставляет с функцией
y(x) функцию известного класса Y(x) E Y(x, a0, a1...an) зависящую от n + 1 параметров aj, выбранных так, чтобы значения Y(x) совпадали со значениями y(x) для данного множества n + 1 значений аргументов xk (узлов интерполяции). Интерполяционная формула n-го порядка аппроксимирует функцию y(x) многочленом n-й степени Y(x), удовлетворяющему условиям Y (xk) = y (x0) = yk в n + 1 узлах интерполяции — точках Xk (x = 1,2...n). [3]Интерполяционная формула Ньютона предполагает наличие равномерно расположенных узлов интерполяции. В практике вычислений данный ряд значений соответствует обычно ряду значений независимого переменного, следующих друг за другом с равными интервалами. Как правило, реальные наблюдения и измерения редко представляют собой такую правильную закономерность. Поэтому формулу Ньютона не будем принимать к рассмотрению. Отметим, что существуют различные формулы интерполирования: Бесселя, Лагранжа, Эйткена… Рассмотрим использование интерполяционной формулы Лагранжа для неравномерно расположенных узлов [3]:
в общем виде:
в частном случае, используя по три узловые точки
y (x) = y [j]? (x – x [j + 1])? (x – x (j + 2)/(x
[j] –
– x [j + 1]) ?
(x [j] – x [j + 2]) + y [j + 1]
? (x – – x [j]) y
(x) = y [j]? (x –
x [j + 1]) ? (x – x
[j + + 2])/(x [j + 1] – x [j])? (x[ j + 1] – x [j + 2]) +
+ y [j + 2] ? (x – x
[j]) ? (x –x [j + 2]) /
(x [j + + 2] – x [j]) ? (x [j + 2] – x [j + 1])
(3)
Это формула квадратичной интерполяции, промежуточные значения сглаживаются, узловые значения остаются исходными.
Алгоритм включает в себя следующее:
1) если аргумент совпадает с каким-либо узлом интерполяции, взять табличное значение функции.
2) иначе определение номера начального узла интерполяции
1 если
x < x [1]
i = n – k
если x > x [n – k]
i
если x [i] < = x < x [i + k], i = 1, 2, 3 ... n – k3) вычисление собственно значения функции
В настоящее время большинство ПК укомплектовано графическими адаптерами
VGA, которые обладают разрешением 640? 480 точек и SVGA с разрешением 800? 600 или 1024? 768 точек и палитрой от 16 до 256 цветов. Исходя из этого, для достижения результата, нам потребуется конечное количество вычислений, для монитора разрешением 640х480 точек потребуется обработать не более 307200 точек.1) считываем или вводим модель сети:
M? N узловых точек, для хаотически расположенных точек целесообразно произвести приведение к некоторой упорядоченной сетке, включающей только точки, попадающие на экран монитора (или виртуальный экран). Это может быть выполнено любым из методов трехмерной интерполяции и не займет много времени, так как объем расчетов невелик2) определяем для узлов экранные координаты
x, y3) вычислим направляющие поверхности, например, параллельные оси
X, для каждой последовательности точек вычислим отметки промежуточных точек, сохраняя данные в памяти для более быстрого доступа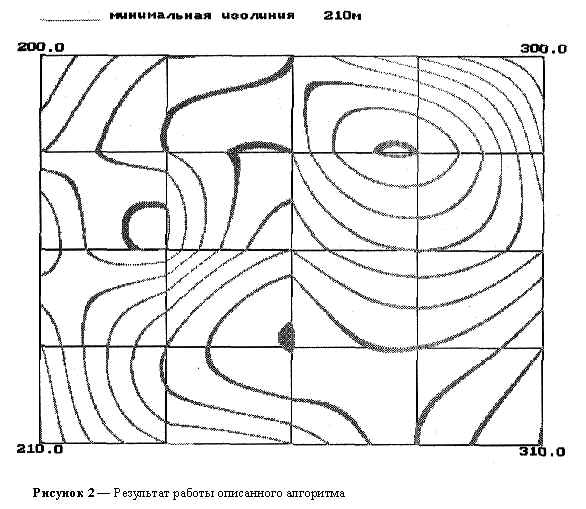
4) в поперечном направлении вычислим координаты экранных точек, вычисленные узлы берутся из соответствующих направляющих
5) в процессе вычисления производится проверка для каждой вычисленной точки на кратность заданному шагу изолиний и, если это условие выполняется (с известной долей погрешности, естественно), то точка прорисовывается.
Рисунок демонстрирует результат работы описанного алгоритма.
Предлагаемый метод визуализации топологической информации иллюстрирует одно из возможных решений проблемы. Он отличается своей простотой, достигает весьма приближенных результатов и имеет следующие достоинства:
| используется один из простейших алгоритмов интерполяции, поэтому вычисления сводятся к минимуму, и прорисовка изолиний поверхности выполняется довольно быстро; | |
| изолинии получаются достаточно гладкими, так как применяется параболическая интерполяция; | |
| достигается значительное сокращение количества вычислительных операций и времени, поскольку в обработку включаются только экранные точки. |
В заключение можно указать некоторые пути совершенствования процесса визуализации. В практике горного дела используются чертежи, в которых могут быть использованы различные по точности методы визуализации топологической информации, дающие различные по степени приближения к реальным поверхностям математические модели.
Любая задача для достижения более точных результатов должна использовать и более точные и сложные методы. Большая гладкость математической модели может быть достигнута использованием кубической сплайн-интерполяции. Сплайны моделируют очень старое механическое устройство. Чертежники издавна пользовались механическими сплайнами, представляющими собой гибкие рейки из какого-нибудь упругого материала, обычно дерева. Механический сплайн закрепляют, подвешивая грузила в точках интерполяции, называемых исторически узлами. Сплайн принимает форму, максимально уменьшающую его потенциальную энергию, и в теории балок устанавливается, что эта энергия пропорциональна интегралу по длине дуги от квадрата кривизны сплайна [5].
С развитием вычислительной техники подобное интерполирование может быть выполнено математическими методами. Другой путь усовершенствования — аппроксимация поверхности треугольниками, вычисление вершин треугольников, вычисление нормального вектора к плоскости каждого из треугольников, наконец, пространственная интерполяция сторон треугольника и как следствие получение некоторых полигонов, объединяющих ступенчатые отметки, затем на их основе сглаживание полигонов с целью получить наиболее гладкие кривые изолиний.
На первый взгляд эта задача покажется очень сложной. Она действительно очень сложная. Для того чтобы практически ее можно было использовать, необходимо ускорение элементарных вычислений, оптимизация алгоритма с целью исключения ненужных преобразований, использование быстрой памяти.
Библиографический список
1.
Мирный В.В. Проекции в маркшейдерском деле. — Киев. — 1994.2.
Омельченко. Справочник по маркшейдерскому делу. — М.: Углетехиздат. — 1953.3. Т. Корн, Г. Корн Справочник по математике для научных работников и инженеров. — М.: Наука. — 1974.
4.
Ф.Мартинес. Синтез изображений. Принципы, аппаратное и программное обеспечение. — М.: Радио и связь, 1990.5.
Л.Аммерал. Принципы программирования в машинной графике. — М.: Сол Систем. — 19926.
Д.И. Ткач. Архитектурное черчение. — Киев. — Будівельник. — 1991.a
В.Ю.Несмеянов, В.В.Мирный, 1999.