Применение изолиний для создания генографических карт

Построенная с помощью интерполяции модель генного рельефа задается двумерной поверхностью, погруженной в трехмерное пространство. Существует несколько методов отображения подобной поверхности на плоскости, из которых наиболее часто используется трехмерная проекция и метод изолиний. Широкое распространение метода изолиний в географии можно объяснить его преимуществами, сочетающими наглядность получаемой модели и легкость решения метрических задач, связанных с восстановлением высоты исходного рельефа в некоторой точке географического пространства. Указанные преимущества относятся также и к геногеографическим картам.

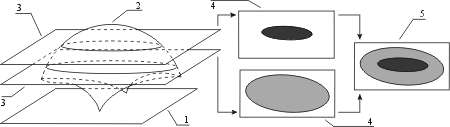
Изолинии на геногеографической карте обозначают геометрическое место точек, для которых интерполяционные значения генных частот равны наперед заданной константе C, т.е. q=f(x,y)=C. В отличие от изолинейной, на интервальной карте область, для которой выполнено неравенство q=f(x,y)>=C, выделяется одним цветом, другим цветом - область точек q=f(x,y)<C (см. Рис. 4. Процедура создания интервальной карты). Если на карте необходимо изобразить несколько интервалов, заданных упорядоченным набором границ интервалов C₁,C₂,C₃,..., то области q=f(x,y)>=C_i последовательно накладываются друг на друга, причем последовательность наложения - от меньших значений C_i - к большим значениям. Легко заметить, что для получения области q>=C_i достаточно построить изолинию q=C_i, а затем ограниченное этой изолинией множество точек q>=C_i на плоскости закрасить требуемым цветом. Однако, прежде чем описывать процедуру построения изолинии, определим понятие цифровой модели генетического рельефа.

Цифровой моделью генетического рельефа (ЦМГР) называется матрица интерполированных значений некоторого генетического признака на равномерной прямоугольной сетке, покрывающей площадь карты. Иными словами ЦМГР - это сеточная функция на плоскости с постоянным шагом Dx по горизонтали и постоянным шагом Dy по вертикали. Использование сеточной функции q_ij=f(x_i,y_j ) в интерполяционных процедурах является общепринятым и связано с рядом преимуществ методического характера. Здесь сочетается удобство хранения полученной информации, возможность ее статистической обработки и математической трансформации будущей карты, а также легкость реализации процедур построения изолиний (в виде ломаной линии) и интервальных областей по значениям интерполирующих функций в узлах сетки.

Все изолинии на карте можно разделить на два типа: замкнутые и незамкнутые, т.е. такие, которые начинаются и заканчиваются на границе сетки. Рассмотрим метод построения незамкнутой изолинии. Первое, что требуется сделать - найти начало незамкнутой изолинии и «завязать траекторию». Условие прохождения изолинии через граничное ребро сетки задается неравенством q_ij<C<q_lm, где q_ij и q_lm - значения функции в соседних узлах (x_i,y_j) и (x_l,y_m) на границе сетки, которые соединяются данным ребром. Особый случай, когда изолиния проходит точно через узел сетки, легко исключить, прибавив к значению сеточной функции в этом узле малую константу, достаточно близкую к нулю. Точные координаты (X₀,Y₀) начальной точки изолинии находятся из системы линейных уравнений как координаты точки пересечения в пространстве плоскости q=C и отрезка, соединяющего точки (x_i,y_j,q_ij) и (x_l,y_m,q_lm). Итак, траектория изолинии завязана, и при этом также определена ячейка, в которую входит изолиния и из которой она должна обязательно выйти, но уже через другое ребро этой ячейки. Чтобы найти координаты следующей точки ломаной изолинии необходимо выделить из оставшихся трех ребер ячейки то, для которого выполнено q_ij<C<q_lm, а затем определить координаты (X₁,Y₁) как решение системы линейных уравнений, описывающих пересечение плоскости q=C и прямой, проходящей через точки (x_i,y_j,q_ij), (x_l,y_m,q_lm), на концах выбранного ребра. После этого можно перейти к следующей ячейке, в которую входит изолиния, и проделать те же самые действия. Описанную итерационную процедуру следует выполнять до тех пор, пока очередная точка пересечения изолинией ребра сетки не окажется на границе сетки. Найденная последовательность точек (X₀,Y₀), (X₁,Y₁), (X₂,Y₂ ),... может быть использована для нанесения изолинии на карту. При составлении интервальной карты требуется определить регион закраски, для чего следует замкнуть изолинию вдоль границы по направлению от первой точки к последней.

Аналогично происходит построение замкнутых изолиний. В этом случае для завязывания траекторий изолиний необходимо просматривать не внешние, а все внутренние ребра сетки, за исключением тех, через которые уже прошли изолинии. Признаком окончания итерационной процедуры построения изолинии можно считать отсутствие ребра, через которое еще не проходит изолиния, и через которое она могла бы выйти из очередной ячейки сетки.

При достаточно густой сетке (в Атласе использована сетка размером 200 точек по горизонтали и 154 точки по вертикали) изолинии получаются гладкими. Впрочем, при необходимости возможно их сглаживание, например, за счет применения сплайнов (Самарский, Гулин, 1989).

Ю.Г. Рычков, О.В. Жукова, А.Н. Евсюков, О.Ю. Наумова, С.Ю. Рычков, В.А. Шереметьева, Ю.В. Шнейдер