Источник: http://selin.kiev.ua/nm/lectures/interpol.html#Теорiя - теория к лабораторной работе учебного комплекса по MathCAD'у в электронном виде.
|
Постановка задачі. Нехай відомі значення функції y = f(x) у декількох точках xi, i = 0, 1, …, n; a < xi < b. Задача полягає у відновленні виду функції f(x) та/або її значень у інших точках з деякою точністю.
Термінологія. Точки xi, i = 0, 1, …, n - вузли інтерполяції, yi - вузлові значення.
Інтерполяція - апроксимація. У такому порівнянні інтерполюванням називається задача відшукання функції f(x) такої, що точно вдовольняє вузловим значенням: f(xi ) = yi , i = 0, …, n.
Апроксимацією називається функція f(x), близька до y лише у тому сенсі. що сумарна помилка S = || f - y || є мінімальною.
Інтерполяція - екстраполяція. У такому протиставленні інтерполяцією називають обчислення значень функції всередині інтервалу [a; b]; екстраполяцією - поза цим інтервалом.
Інтерполяційні поліноми. Поліном Pn(x) степеня n, що точно вдовольняє вузловим значенням, існує та є єдиним. Для його відшукання треба розв’язати систему
|
|
Pn(x0) = an x0n + an-1x0n-1 + … + a1 x0 + a0 = y0; |
|
… | |
| Pn(xn) = an xnn + an-1xnn-1 + … + a1 xn + a0 = yn; |
відносно коефіцієнтів an, …, a0. Для спрощення задачі існують певні форми запису цього поліному.
Нехай
|
|
- функція; | (0) |
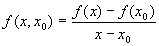 |
- поділена різниця; | (1) |
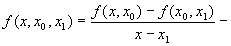 |
- друга поділена різниця; | (2) |
f(x) = f(x0) + (x - x0) f(x, x0);
f(x, x0) = f(x0, x1) + (x - x1) f(x, x0, x1);
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x, x0, x1);
Аналогічно:
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x, x0, x1) + (x - x0) (x - x1) (x - x2) f(x, x0, x1, x2);
…
f(x) = f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x0, x1, x2) + (x - x0) (x - x1) (x - x2) f(x0, x1, x2, x3) + … + (x - x0) (x - x1)… (x - xn-1) f(x0, x1,…, xn) + (x - x0) (x - x1)… (x - xn) f(x, x0,…, xn) ,(3)
причому підкреслена частина є деяким поліномом n-го порядку:
f(x0) + (x - x0) f(x0, x1) + (x - x0) (x - x1) f(x0, x1, x2) + (x - x0) (x - x1) (x - x2) f(x0, x1, x2, x3) + (x - x0) (x - x1)… (x - xn-1) f(x0, x1,…, xn) = Pn(x).
Якщо x = x0, x1, …, xn, то f(xi) = Pn(xi) = yi, тому що (x - x0) … (x - xn) f(x, x0, …, xn) = 0!
Права частина виразу (3) і є інтерполяційним поліномом Ньютона.
Якщо x0 < x1 < … < xn, то це – формула інтерполяції вперед, якщо навпаки –назад.
Pn(x) = f(xn) + (x - xn) f(xn, xn-1) + (x - xn) (x - xn-1) f(xn, xn-1, xn-2) + (x - xn) (x - xn-1) (x - xn-2) f(xn, xn-1, xn-2, xn-3) + (x - xn) (x - xn-1)… (x - x1) f(xn, xn-1,…, x0) -
- інтеполяційний поліном "назад".
rn(x) = f(x) - Pn(x).
Нехай
![]()
та
g(s) = f(s) - Pn(s) - k w(s),
де
w(s) = (s - x0) (s - x1) … (s - xn).
При s = xi, i = 0, 1, …, n, w(xi) = 0. Тому g(xi) = 0, бо f(xi) = Pn(xi). Виберемо деяку точку x № xi, i = 0, 1, …, n, та виберемо k так, щоби g(x) = 0. Тоді
0 = f(x) - Pn(x) - k w(x);
k = (f(x) - Pn(x)) / w(x);
Враховуючи, що w(n+1)(s) = (n+1)!, та те, що g(s) має n+2 нулі на [a;b], то g'(s) має n+1 нуль, g''(s) має n нулів, … g(n+1)(s) має принаймні один нуль. Нехай це має місце при s = x. Тоді
![]()
![]()
|
| (4) |
Розгляньмо функцію Wi (x) = (x - x0) (x -
x1) … (x - xi-1) (x - xi) (x -
xi+1) … (x - xn).
У ній відсутній член (x - xi), тому при x = xi вона приймає ненульове значення. Якщо її пронормувати значенням Wi (xi), то одержуємо т.зв. фундаментальний поліном Лагранжа
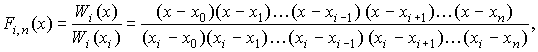
причому
| Fi,n(xj) = | { | 1 при x = xj, j <> i; | } | = dij при x = xj. |
| 0 при x = xi; |
Тоді
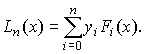
Поліном Лагранжа повністю збігається з інтерполяційним поліномом Н’ютона - це дві форми запису того самого єдиного поліному.
У вузлах може бути задано значення функції f та похідні - f', f'', …, f(Ni-1) - усього Ni штук.
Тоді всього буде N0 + N1 + … + Nn умов.
Шукається поліном степеня
![]()
у якому Ni - кратність вузла і.
Поліном існує та єдиний. Кількість рівнянь дорівнює кількості коефіцієнтів. Розгляньмо поліном степеня m, похідні якого Hm(j)(xi) = 0, j = 0, 1, …, Ni . Це означає. що xi - корінь кратності Ni .
Тоді на [a; b] існує N0 + N1 + … + Nn = m+1 коренів. але степінь його m, тому при всіх x Hm(x) = 0.
Будемо шукати Hm(x) у вигляді
Hm(x) = Ln(x) + wn(x) Hm-n(x),
де
Ln(xi) = yi, wn(xi) = 0, i = 0, 1, …, n.
Похідна:
H'm(x) = L'n(x) + w'n(x) Hm-n(x) + wn(x) H'm-n(x),
причому
H'm(xi) = L'n(xi) + w'n(x) Hm-n(xi).
У тих точках. де задано f'(xi), знайдемо
![]()
Далі шукають другу похідну
H''m(x) = L''n(x) + w''n(x) Hm-n(x) + 2 w'n(x) H'm-n(x) + wn(x) H''m-n(x),
причому
H''m(xi) = L''n(xi) + w''n(xi) Hm-n(xi) + 2 w'n(xi) H'm-n(xi),
Звідки виражають H'm-n(xi), тому що інші величини є відомими, і т. ін..
Приклад.
Нехай задано значення функції та її похідних у точках
x0 = 0; x1 = 1; x2 = 2:f(0) = 1; f '(0) = 1; N0 = 2;
f(1) = 1,5; N1 = 1;
f(2) = 0; f '(2) = 0; f ''(2) = 1; N0 = 2;
Таким чином,
m = (2 + 1 + 3) - 1 = 5. Поліном Ерміта шукаємо у вигляді H5(x) = L2(x) + w3(x) H2(x):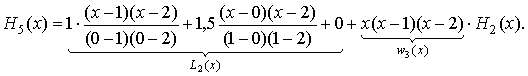
![]() ,
,
тому
![]()
w3'(x) = (x - 1)(x - 2) + x(x - 2) + x(x - 1);
w3'(0) = 2; w3'(1) = -1; w3'(2) = 2;
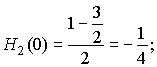
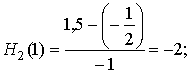
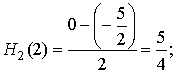
H5''(x) = -2 + w3''(x) H2(x) + 2w3'(x) H2'(x) + w3(x) H2''(x);
H5''(2) = -2 + w3''(2) H2(2) + 2w3'(2) H2'(2) + w3(2) H2''(2);
1 = -2 + 6(2-1) 5/4 + 4 H2''(2) + 0;
H2'(2) = -1,125. Далi є арифм. помилки...
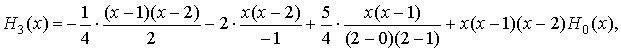
H0(x) = const.
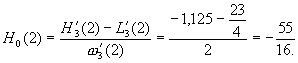
Збіжність процесу інтерполяції.
Розглянемо послідовність сіток
wn:a = x0 < x1 < … < xn-1 < xn = b.
При
max (xn - xn-1) 0 для заданої f(x)Теорема Фабера.
Для будь-якої послідовності сіток wn знайдетьсяТеорема Марцинкевича. Для
Поліноміальним сплайном порядку m та дефекту k називається функція Sm,k(x) на сітці
a = x0 < x1 < … < xn-1 < xn = b
така, що:
Розгляньмо сплайн дефекту 1.
Sm,1 = Sm.Інтерполяційним сплайном називається
Sm(x):Усього вільних коефіцієнтів:
N(m+1).Умов неперервності:
(N-1)m (похідні від f (0) = f до f (m-1)).Умов інтерполяції:
N+1 типу 3).Усього
N(m+1)-(N-1)m-N-1=N+m-N-1=m-1.Систему недовизначено. Можна задати додатково крайові умови у точці х
= а та х = b.Розглянути приклад:
m = 0 – кусочно-постійна функція; m = 1 - кусочно-лінійна; m = 3 - кубічні сплайни.Доведено збіжність
Представлення у формі Лагранжа:
![]()
F - фундаментальні сплайни:
![]()
Сплайни
F є незручними; їхній вигляд є заскладним; щоб їх визначити, слід розв'язати таку ж задачу.Зручніше –
B-сплайни:Bm,i(t) - сплайн порядку m дефекту 1.
Bm,i(j)(ti) = Bm,i(j)(ti+m+1) = 0 та за межами [ti, ti+m+1]; j=0, 1, …, m-1.
 .
(5)
.
(5)
При цьому виявляється, що,
B(x) > 0 при хКількість умов:
- 2m умов на кінцях;
- m*m умов неперервності f, f ', f '', …, f(m-1) в m серединних вузлах; усього m2 + 2m;
- коефіцієнтів
(m + 1)2 = m2 + 2m + 1.Тому умова (5) нормалізує
B-сплайн.Існує рекурентна формула:
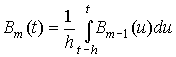
де
Bm = Bm,0.Решта – зсувом.
На сітці
a = x0 < x1 < … < xn-1 < xn = b для інтерполяції слід використовувати сплайни { Bm,i }, i = -m, …, N-1, усього N + m = (N + 1) + (m - 1), тобто дефект визначеності той самий. Вони утворюють базис у просторі S-сплайнів на цій сітці.Наприклад,
B3,i на сітці x0, …, xn використовуються від B3,-3 до B3,N-1 - всього N + 3 на (N + 1) точках.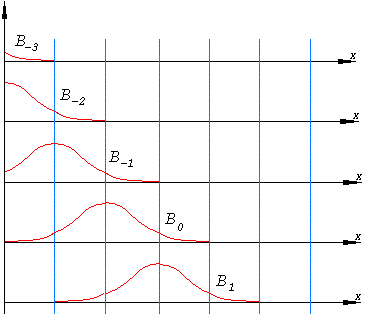
Нерівномірний B3,0 - сплайн.
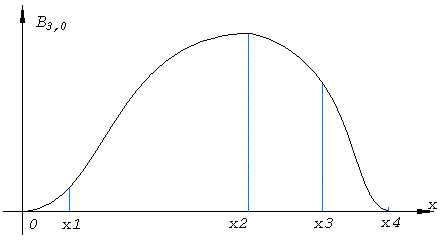
B(x1) = a1x13 + b1x12 + c1x1 + d1 = a0x13.
B'(x1) = 3a1x12 + 2b1x1 + c1 = 3a0x12;
B''(x1) = 6a1x1 + 2b1 = 6a0x1;
B(x2) = a1x23 + b1x22 + c1x2 + d1 = a2x23 + b2x22 + c2x2 + d2.
B'(x2) = 3a1x22 + 2b1x2 + c1 = 3a2x22 + 2b2x2 + c2;
B''(x2) = 6a1x2 + 2b1 = 6a2x2 + 2b2;
B(x3) = a3(x4 - x3)3 = a2x33 + b2x32 + c2x3 + d2;
B'(x2) = - 3a3(x4 - x3)2 = 3a2x32 + 2b2x3 + c2;
B''(x2) = 6a3(x4 - x3) = 6a2x3 + 2b2;