Численные методы математического анализа
1. Задача интерполяции. Многочлен Лагранжа
1.1. Постановка задачи
Пусть задана функция ![]() . Часто нахождение
значений этой функции может оказаться трудоемкой задачей. Например,
. Часто нахождение
значений этой функции может оказаться трудоемкой задачей. Например, ![]() - параметр в
некоторой сложной задаче, после решения которой определяется значение f(x), или
f(x) измеряется в дорогостоящем эксперименте. В этих случаях можно получить
небольшую таблицу значений функции, но прямое нахождение ее значений при большом
количестве значений аргумента нереально. В такой ситуации f(x) заменяется
приближенной формулой
- параметр в
некоторой сложной задаче, после решения которой определяется значение f(x), или
f(x) измеряется в дорогостоящем эксперименте. В этих случаях можно получить
небольшую таблицу значений функции, но прямое нахождение ее значений при большом
количестве значений аргумента нереально. В такой ситуации f(x) заменяется
приближенной формулой ![]() , которая в
определенном смысле близка к функции f(x). Близость обеспечивается введением в
функцию
, которая в
определенном смысле близка к функции f(x). Близость обеспечивается введением в
функцию ![]() свободных параметров и их
соответствующим выбором.
свободных параметров и их
соответствующим выбором.
Итак, известны значения функции f(x) в точках ![]()
![]() ,
,
![]() . Потребуем, чтобы для некоторой функции
. Потребуем, чтобы для некоторой функции ![]()
выполнялись равенства:
![]()
![]() (1)
(1)
Если (1) рассматривать как систему для определения ![]() , то этот
способ называется интерполяцией (Лагранжевой).
, то этот
способ называется интерполяцией (Лагранжевой).
Если ![]() зависит от
зависит от ![]() нелинейно, то
интерполяция нелинейная, иначе интерполяция линейная. В случае линейной
интерполяции можно записать
нелинейно, то
интерполяция нелинейная, иначе интерполяция линейная. В случае линейной
интерполяции можно записать
 (2)
(2)
(где ![]() - система
линейно-независимых функций)
- система
линейно-независимых функций)
Подставим (2) в (1). Относительно ![]() получаем линейную
систему уравнений:
получаем линейную
систему уравнений:
 ,
,
![]() (3)
(3)
Для однозначной разрешимости системы должно быть ![]() .
.
Для того, чтобы задача нтерполирования имела единственное
решение, система функций ![]()
![]() должна для любых
несовпадающих
должна для любых
несовпадающих ![]() удовлетворять условию:
удовлетворять условию:
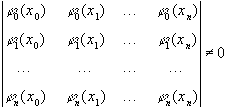 (4)
(4)
Система функций, удовлетворяющая условию (4), называется чебышевской.
Наиболее простой и (для многих случаев) удобной является
система функций ![]() ,
, ![]() . Функция
. Функция ![]() при этом представляет
собой многочлен степени
при этом представляет
собой многочлен степени ![]() (интерполяционный
многочлен) с коэффициентами
(интерполяционный
многочлен) с коэффициентами ![]() .
.
Система уравнений (3) в этом случае имеет вид:
 ,
,
![]() (5)
(5)
Определителем этой системы является отличный от нуля
определитель Вандермонда: 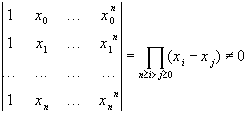
Отсюда следует, что интерполяционный многочлен существует и единственен.
Непосредственное решение системы (5) для нахождения
aj уже при небольших n приводит к сильному
искажению значений aj. Получим явный вид
нтерполяционного многочлена  , не решая систему
(5).
, не решая систему
(5).
Если ![]() многочлен степени n
такой что
многочлен степени n
такой что ![]() , то
, то 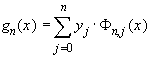 - искомый интерполяционный многочлен степени
- искомый интерполяционный многочлен степени ![]() , т.к.
, т.к. 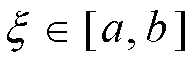 .
.
Так как ![]() при
при ![]() , то
, то ![]() делится на
делится на ![]() для любых
для любых
![]() , то
есть
, то
есть
![]() . Так как
. Так как ![]() , то
, то 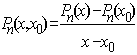 .
.
Таким образом,![]() (6)
(6)
Такая форма записи интерполяционного многочлена называется
многочленом Лагранжа и обозначается, как правило, ![]() .
.
Существуют и другие формы записи того же самого интерполяционного многочлена.
Если обозначить ![]() , то
, то
![]() .
.
Тогда (6) можно записать в виде 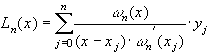
В узлах ![]() многочлен Лагранжа
совпадает с заданной функцией, в остальных точках в общем случае
многочлен Лагранжа
совпадает с заданной функцией, в остальных точках в общем случае ![]() не совпадает с
не совпадает с ![]() (кроме
случая, когда
(кроме
случая, когда ![]() многочлен степени не выше
многочлен степени не выше ![]() ). Разность
). Разность ![]() -
- ![]() - остаточный член. Запишем ее в виде
- остаточный член. Запишем ее в виде ![]() .
.
При ![]() . Найдем постоянную
такую, чтобы
. Найдем постоянную
такую, чтобы ![]() в некоторой фиксированной точке
в некоторой фиксированной точке ![]() , в которой мы
рассматриваем погрешность.
, в которой мы
рассматриваем погрешность.
Относительно ![]() будем предполагать
будем предполагать ![]() кратную
дифференцируемость.
кратную
дифференцируемость.
Значение c, при котором ![]() существует и равно
существует и равно ![]() . Тогда
функция
. Тогда
функция ![]() равна нулю по крайней мере в
равна нулю по крайней мере в ![]() точках
точках ![]() .
.
По теореме Ролля производная ![]() равна нулю по крайней
мере в
равна нулю по крайней
мере в ![]() точках
точках ![]() . Далее,
. Далее, ![]() равна нулю по крайней мере в n точках и т.д.
равна нулю по крайней мере в n точках и т.д.
Для ![]() - производной получаем,
что существует по крайней мере одна точка
- производной получаем,
что существует по крайней мере одна точка ![]() такая, что
такая, что ![]() .
.
![]()
Отсюда получаем при ![]() . В этом случае в
точке
. В этом случае в
точке ![]()
![]() , т.е. остаточный член в точке
, т.е. остаточный член в точке ![]() имеет вид:
имеет вид:
![]()
Значение![]() зависит от
зависит от ![]() - точки, в
которой рассматривается погрешность.
- точки, в
которой рассматривается погрешность.
![]() ,
,
где ![]()