1. Методы и алгоритмы формирования контурных изображений
2.
Интерполяция и
аппроксимация кривых произвольного типа
3. Сплайновая интерполяция
Методы
аппроксимации функций с помощью сплайнов, предложенные впервые в 40-х
годах, получили широкое распространение только в последнее время.
Основной
недостаток интерполяционных многочленов как аппарата приближения функций,
применяемого для восстановления дискретизированных сигналов, состоит в
том, что поведение этих многочленов в окрестности какой-либо точки
определяет их поведение в целом. Если исследуемый сигнал на разных
участках ведет себя по-разному, например на одном участке постоянен, а
затем круто убывает или возрастает и т.д., использование интерполяционных
многочленов хороших результатов не дает. В таких случаях лучше
пользоваться сплайнами.
Английское
слово spline означает «упругая рейка». Такую рейку используют в
качестве гибкого лекала при вычерчивании плоских кривых по опорным
точкам.
Основная
идея применения сплайнов состоит в следующем.
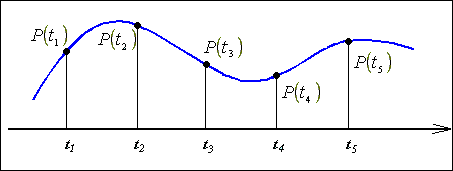
Рис. 1.16. Восстановление сигналов при помощи
сплайнов.
При этом важным условием является также
непрерывность нескольких производных. Таким образом, сплайном
Pn
называют совокупность многочленов Pni
степени n, заданных
на i-том шаге дискретизации и
удовлетворяющих условию
Pni(ti)
= Pn(i-1)(ti),
т.е.
степени n
сплайн-функциями,
составленными из «кусочков» многочленов данной степени, которые
состыкованы так, чтобы получившаяся функция была непрерывной и имела
несколько непрерывных производных.
Таким
образом, сплайн является кусочно-полиномиальной функцией. Сплайн нулевой
степени совпадает со ступенчато-интерполированной функцией, а сплайн
первой степени – с линейно-интерполированной. Следует отметить, что
сплайны второй и более высокой степени не будут совпадать с
интерполяционными полиномами соответствующих степеней.
Известно,
что когда однородный брус закрепить в двух произвольных точках и предать
его оси заданный наклон в этих точках, то форма кривой бруса описывается
полиномом третьей степени.
Предположим, что кубическая парабола, заданная в параметрической
форме
P(t) = a3t3 + a2t2 + a1t + a0
проходит через две точки P(t1) и P(t2), в которых известны значения производных
Р/(t1)
и Р/(t2). Это означает, что заданы четыре необходимых
и достаточных условия для определения четырех неизвестных коэффициентов в
приведенном выше выражении. Этот многочлен называют кубическим
интерполяционным многочленом Эрмита.
Параметрическое представление кривой имеет то преимущество, что
можно выбрать произвольный диапазон изменения параметра. Для простоты
вычислительного процесса будем считать, что параметр t в пределах
каждого сегмента изменяется в диапазоне от 0 до
1
(0ЈtЈ1).
Нетрудно
заметить, что
Определим
производную Р/(t): Р/(t)=3a3t2+2a2t+
a1.
Отсюда следует,
что
Из приведенных
выражений легко определить неизвестные a0, a1, a2,
a3:
a0=P(0),
a1=Р/(0),
a2=3
Рассмотренная процедура выполняется для
каждой пары заданных точек кривой. Так, определив кубическую параболу
между точками P(t1) и P(t2)
на интервале t1t2, для
нахождения следующей дуги кривой на интервале t2t3 необходимо на границе интервала (точка
t2)
приравнять значения как самих кривых, так и их первых производных, т.е.
выполнить “склеивание”.
Определим
выражение для кубической кривой X(t)
в форме Эрмита в матричной форме, если
известны конечные точки и касательные вектора к кривой в этих точках.
Определим,
что Р1, Р4 – точки;
R1,
R4 –
касательные.
X(0) = P1x
X(1) = P4x
X(0) = R1x
X(1) = R4x
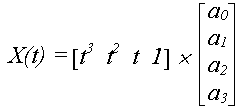
или
X(t) = TCx (*),
где T
=
[t3,
t2,
t,
1],
X(0) = P1x = [0,0,0,1]Cx,
X(1) =
P4x = [1,1,1,1]Cx
,
X/(t) =
[3t2,
2t, 1, 0]Cx,
X/(0) = R1x = [0,0,1,0]Cx,
X/(1) = R4x = [3,2,1,0]Cx.
P1 0, 0, 0, 1
P4 1, 1, 1, 1
R1 0, 0, 1, 0
R4
3, 2, 1, 0
Обращая матрицу размером 4x4,
получаем
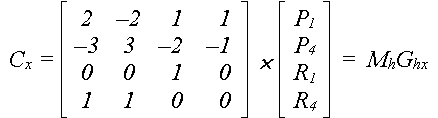
Mh
– называется
матрицей Эрмита, Ghх
– геометрическим
вектором Эрмита.
Подставив
Сx
в (*), получим:
Найдем произведение
ТМ:
Перемножая это выражение справа на
Ghx, получим:
Четыре
полученных функции иногда называют функциями сопряжения.
С помощью
первых двух функций определяются точки Р1 и
Р4, а с помощью других получим сглаженное объединение.
Чем больше касательный вектор, тем круче сама кривая.
К
недостаткам такого подхода следует отнести необходимость задания
производных в узлах. Для их нахождения используют ряд подходов.
Наиболее
просто использовать вместо производных их приближенные значения,
полученные в результате других аппроксимаций. Например, для каждого узла
по значениям функций в ближайших 2m
узлах строится многочлен степени
2m+1,
производные которого затем используются для построения эрмитового
сплайна.
При
представлении кривой в форме Безье для нахождения производных
P/(ti)
и
P/(ti+1) используются две
дополнительные точки (рис.1.17) Ri
и Ri+1, которые задают два касательных вектора
P(ti)Ri
и P(ti+1)Ri+1.
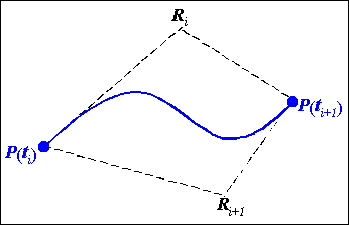
Рис. 1.17. Нахождение поризводных по методу Безье
Производные P/(ti) и P/(ti+1)
определяют по следующим выражениям:
R1=3(P2–P1)=P’(0),
R4=3(P4–P3)=P’(1).

Это соотношение между матрицей Эрмита
Gh и геометрической матрицей Безье. Подставляя
полученные значения, получаем
Обозначив произведение MhMb
через
М
получаем
соотношение X(t)=TMGb, которое имеет форму Бєзье.

Форма
Безье используется в машинной графике чаще, чем форма Эрмита. Причины в
следующем:
* во-первых, в случае формы Эрмита касательные векторы должны задаваться в явном виде. В форме Безье касательные находят “локатором”;
* во-вторых, в форме Безье четыре
точки задают выпуклый многоугольник, который можно выполнить резиновой
нитью.
Определим Х =
TMbGb.
Можно показать, что сумма всех коэффициентов
при t
равна 1, что определяет
оптимальное среднее значение для четырех управляющих точек.
Разработан подход, согласно которого производные в
промежуточных точках находят путем решения матричного уравнения
вида:

Подход
основан на равенстве первых и вторых производных на границах интервалов.
Из приведенного матричного выражения находят производные, представленные
второй матрицей в левой части уравнения. Таким образом в рассматриваемом
подходе в качестве исходных задаются все базовые точки, через которые
проходит кривая, а также производные в начальной и конечной точках.
Другие
способы получения недостающих параметров для построения сплайнов основаны
на наложении некоторых дополнительных условий, что приводит к
необходимости решения системы уравнений, выражающей эти условия.
В
общем случае, когда в моменты времени e=0,1,2,…
заданы дискретные отсчеты сигнала
x0,
x1,
x2,…, восстанавливающая дискретизированный сигнал
сплайн-функция n-ой степени имеет вид
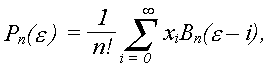
где Bn(e)
– некоторый сплайн степени n
(B-сплайн Шенберга)
и называемый ядром сплайна. Функция Bn(e)
описывается следующим
образом:

где C![]() – число сочетаний из (n+1)
по
k.
– число сочетаний из (n+1)
по
k.
При
переходе от интерполяции многочленами к интерполяции сплайнами
преследуются две цели. Первая, это улучшение качества приближения: при
одинаковых вычислительных затратах абсолютные погрешности интерполяции
сплайнами меньше, чем погрешности интерполяции многочленами, а при
одинаковых погрешностях уменьшается объем вычислений. Сплайны позволяют
избежать осцилляций. Для решения задачи сходимости предъявляются более
слабые требования, чем в случае многочленов. Например, интерполяция
сплайнами невысоких степеней сходится даже для непрерывных функций.
Вторая
цель – резкое уменьшение вычислительных затрат, поскольку при построении
алгоритмов решения задач, так и при дальнейшей работе с аппроксимантами
используются многочлены невысоких степеней или иные элементарные
функции.
При работе со сплайнами можно использовать либо кусочно-многочленное представление, либо представление через базисные функции. В первом случае достигается наибольшая экономия в числе арифметических операций, но зато приходится хранить большой объем информации о многочленах. Во втором случае имеем обратное.