Введение

Основными источниками ошибок растрового изображения являются нели-нейная деформация основы, на которой отпечатан исходный материал (бумага, фотобумага, пластик и т.д.) и погрешности сканирующего устройства. Для фото-материалов к этим источникам можно добавить неперпендикулярность оси фото-камеры фотографируемой земной поверхности (наклон снимка), несоответствие (или неточное соответствие) масштаба снимка масштабу создаваемой карты, а также поправки за рельеф, кривизну Земли, рефракцию воздушных масс, дистор-сию объектива камеры и т.д.

Целью трансформирования растра является устранение этих ошибок. Боль-шинство методов трансформирования растровых изображений (далее растров) предполагают получение набора параметров трансформирования по набору опорных точек. Наиболее часто используемым является получение параметров трансформирования по методу наименьших квадратов. При этом получаемые па-раметры позволяют выполнять трансформирование с определенной ошибкой. В результате изображение равномерно "садится" на опорные точки с точностью до указанного допуска (допустимая погрешность опоры - это наибольшее разрешен-ное расхождение между реальными и вычисленными координатами точки). Сле-довательно, изображение опорной точки на трансформированном растре, отлича-ется от ее истинного положения. Увеличивая число опорных точек и количество измерительных итераций можно снизить величину расхождения. Но даже при зна-чительном увеличении числа опорных точек не удается получить параметры трансформирования позволяющие получить нулевую ошибку. В тоже время, про-должительность процесса трансформирования растрового изображения напря-мую зависит от количества опорных точек.

Необходимо дополнительно сказать о создании цифровых растровых карт, получаемых в результате "сшивки" нескольких растров. Ошибки в полосе "сшив-ки", по сравнению с ошибками внутри одного снимка, возрастают, поскольку каж-дый растр трансформировался по своим параметрам. Обычно имеет место сдвиг изображения на границе растров, даже при наличии общих опорных точек между ними.

Для повышения точности трансформирования и устранения вышеуказанных ошибок, в ГИС Карта 2000 реализован простой, но довольно эффективный метод трансформирования растра. Суть метода состоит в разбиении исходного растра на отдельные участки и последующего трансформирования каждого участка. При этом алгоритм трансформирования обеспечивает сведение изображения на гра-ницах участков. Это свойство алгоритма используется при создании мозаичных изображений из нескольких трансформированных растров. При наличии общих точек между растрами алгоритм обеспечивает максимально точное сведение изо-бражения между ними по линии, соединяющей эти общие точки.

При выполнении процедуры трансформирования и получения единого рас-трового пространства будем различать "сшивку" изображения карт и снимков. Поскольку в растровое изображение снимков должны быть внесены поправки за элементы ориентирования и рельеф. Это отдельная процедура, которую необхо-димо выполнить до применения рассматриваемого метода и создания единого растрового пространства.

Алгоритм трансформирования растра.

Для трансформирования по предлагаемому методу необходимо получить набор опорных точек в системе координат растра и соответствующий ему набор точек в истинной системе координат, к которой выполняется трансформирование (в качестве опорных используются точки хорошо распознаваемые на исходном изображении). Точки в истинной системе координат будем называть теоретиче-ским набором. При выполнении процедуры теоретический набор удобнее всего иметь в виде отдельного файла, а измерения точек по изображению выполнять в порядке следования, который в нем описан. В ГИС Карта 2000 после измерения первых двух точек, осуществляется первичная привязка растра, и в дальнейшем "выезд" в район измеряемой опорной точки происходит автоматически, оператор только уточняет ее положение. После измерений выполняется разбиение растра на элементарные треугольные участки, в вершинах которых находятся опорные точки.

Отличительной чертой предлагаемого метода трансформирования является процесс разбиения рабочего поля растра на отдельные участки треугольной фор-мы. Авторы предлагают разбивать растр на треугольники, удовлетворяющие ус-ловиям теоремы Делоне о пустом шаре. Применительно к двумерному простран-ству формулируется она следующим образом: система взаимосвязанных непере-крывающихся треугольников имеет наименьший периметр, если ни одна из вер-шин не попадает внутрь ни одной из окружностей, описанных вокруг образован-ных треугольников. Это означает, что образовавшиеся треугольники максимально приближаются к равносторонним, а каждая из сторон образовавшихся треуголь-ников из противолежащей вершины видна под максимальным углом. Такая триан-гуляция является оптимальной для выполнения любых операций моделирования.

Алгоритмы построения триангуляции Делоне довольно подробно описаны в литературе, в том числе и в публикациях Информационного бюллетеня ГИС Ас-социации.[1,2] Мы не будем подробно рассматривать ни один из них. Скажем лишь что, исследовав несколько вариантов, мы остановились на комбинаторном алгоритме построения триангуляции, как наиболее быстром, а главное, абсолют-но надежном.

Имея два логически связанных множества точек, можно получить две систе-мы треугольников, связанных по определенному логическому признаку. В случае трансформирования растра есть множество точек на местности, с априорно из-вестными координатами и множество точек, полученных в результате измерений растра. Логическая связь множеств устанавливается в момент выполнения изме-рительных операций. В результате получаем систему треугольников, в вершинах которых лежат истинные точки местности и логически связанную с ней систему треугольников, в вершинах которой лежат точки, измеренные по растру.

Далее происходит пересчет координат (трансформирование) каждой точки изображения. Для этого определяют треугольник, которому принадлежит текущая трансформируемая точка растра, и выполняют трансформирование этой точки по алгоритму трансформирования треугольников, в основе которого лежит алгоритм трансформирования отрезка.
Геометрический смысл трансформирования отрезка состоит в том, что вы-полняется параллельный перенос, масштабирование и поворот отрезка AB так, чтобы точка A совпала с точкой A1, а точка В совпала с точкой В1 (рис.1)

рис.1

Аналитически эта зависимость определяется формулой:

x0t = xt1 + k*[ (x0-x1)*cos(-a) + (y0-y1)*sin(-a)];
y0t = yt1 + k*[-(x0-x1)*sin(-a) + (y0-y1)*cos(-a)];

где a- угол между прямыми;
      (x1, y1) - координаты точки A
      (x2, y2) - координаты точки B
      (x0, y0) - координаты произвольной точки N, на отрезке AB
      (x1t, y2t) - координаты точки A1
      (x2t, y2t) - координаты точки B1
      (x0t, y0t) - координаты вычисляемой точки N1
      k - коэффициент сжатия отрезков.

Рассмотрим алгоритм трансформирования треугольника. Пусть в прямо-угольной декартовой системе координат имеются два треугольника с известными координатами вершин А(x1,y1) B(x2,y2) C(x3,y3) и А1(x1t,y1t) B1(x2t,y2t) C1(x3t,y3t). (рис.2). Под трансформированием треугольника АBC в треугольник А1B1C1 будем понимать получение строгих математических зависимостей, по которым для лю-бой точки N (x0, y0) принадлежащей треугольнику АBC можно найти координаты точки N1(x0t, y0t) принадлежащей треугольнику А1B1C1, таких что, точка А транс-формируется в точку А1, точка B в точку B1, а точка C в точку C1.

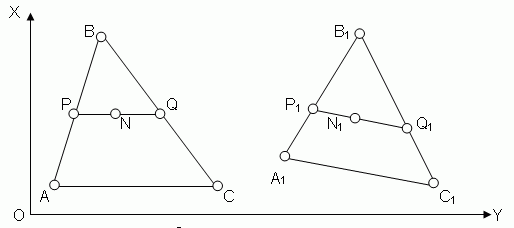
рис. 2

По известным из аналитической геометрии формулам определим уравнение прямой проходящей через точку N параллельной одной из сторон треугольника АBC, например стороне АC (на самом деле выбор стороны не важен, результат трансформирования будет одинаков). Найдем координаты точек пересечения по-строенной прямой с остальными сторонами треугольника. Это точки P(x1с,y1с) и Q(x2с,y2с). Координаты точки P1(x1tс,y1tс) определяются по алгоритму трансформи-рования отрезка. Исходными данными для расчетов являются координаты гра-ничных точек отрезков АB и А1B1 и точка P. Координаты точки Q1(x2tс,y2tс) опреде-ляются по отрезкам BC и B1C1 и точке Q. И, наконец, найдем искомые координаты точки N1 по отрезкам PQ и P1Q1 и координатам точки N. При таком алгоритме трансформирования любая сторона треугольника АBC будет трансформирована в соответствующую сторону треугольника А1B1C1. Ясно, что если в качестве транс-формируемой точки взять какую-либо вершину треугольника АBC, например А, то она принадлежит отрезку АB и значит, по алгоритму трансформирования отрезков будет трансформирована в точку А1.

Методика использования предлагаемого алгоритма трансформирования для получения единого растрового пространства.

Математический аппарат предлагаемого метода трансформирования осно-вывается на системе линейных уравнений первого порядка. Поскольку вычисле-ния производятся внутри элементарной обрасти ограниченной тремя точками, нет возможности оценить степень пригодности точки для вычислений, любая из изме-ренных точек участвует в процессе трансформирования растра. При увеличении длины ребер отдельных треугольников, по сравнению с остальными, это может привести к появлению изломов на границе такого треугольника. Другими словами, без учета пригодности точки для вычислений, алгоритм работает идеально в слу-чае приблизительно равномерного распределения точек по рабочему полю рас-тра. Для устранения данного недостатка предлагается либо выполнять предвари-тельную оценку пригодности точек для трансформирования либо использовать комбинированный метод. Комбинированный метод заключается в сочетании двух вариантов трансформирования. Вначале выполняется трансформирование по методу наименьших квадратов, затем по предлагаемому методу. В результате привязка к местности и оценка пригодности точек для трансформирования выпол-няется в ходе первого трансформирования, а доведение растра по точности пла-нового положения опорных точек в ходе второго.

Разбиение рабочего поля растра на элементарные участки, позволяет по-лучать частные параметры трансформирования, внутри каждой области по трем точкам. Следовательно, другие точки не оказывают влияния на точность транс-формирования элементарного участка. Это положительное качество алгоритма налагает ограничение на его использование. За пределами естественного выпук-лого контура, образованного граничными точками набора, трансформирование по указанному алгоритму выполнить невозможно. Участки растра, лежащие вне замкнутого контура, трансформируются по методу наименьших квадратов. Таким образом, для получения мозаичного изображения, состоящего из нескольких рас-тров необходимо наличие полосы перекрытия соседних растров, с одноименными опорными точками.

Поскольку трансформирование производится к координатам местности из-вестным априорно, то независимо от того, какие параметры трансформирования определялись внутри элементарной области, узловые (опорные) точки и ребра триангуляции трансформируются с нулевой ошибкой. Это свойство предлагаемо-го алгоритма, закладывает возможность формирования единого растрового про-странства из набора смежных растров, уже на этапе трансформирования одного растра. Таким образом, можно получать "сшитое" изображение на любое количе-ство растров. Если при "сшивке" двух и более растров, с использованием пред-лагаемого алгоритма, все равно присутствует сдвиг изображения по границе "сшивки", необходимо добавить дополнительные точки в систему пары триангу-ляций. В случае отсутствия в полосе перекрытия одноименных опорных точек, также проводится поиск одноименных контуров на смежных растрах. Для этого в зоне перекрытия производятся измерения одинаково читаемых контуров местно-сти на обоих растрах (не являющихся опорными точками). По результатам изме-рений выполняется уравнивание, и новые точки добавляются в исходный массив. Происходит перестроение триангуляции в зоне перекрытия и повторное транс-формирование растров, только в зоне измененных треугольников. Использование предлагаемой методики позволяет получать "сшитые" растры без сдвига изобра-жения.

Указанная технология реализована в ГИС Карта 2000. Применение транс-формирования растров, по описанной методике позволило получать цифровое изображение топографической карты, с ошибкой трансформирования по опорным точкам, зависящей только от точности наведения измерительной марки. При вы-полнении измерений изображения опорной точки на достаточно крупном увеличе-нии, СКО опорных точек стремится к нулю. Для создания единого растрового про-странства необходимо выполнить трансформирование каждого из одиночных рас-тров. Далее, для наиболее достоверного представления информации, выполняет-ся операция установления границ визуализации по тем точкам, которые являются общими.

Использование указанной методики трансформирования позволило полу-чать фотопланы, в том числе и орто, из нескольких снимков, различной проекции. На первом этапе производится трансформирование одиночного фотоснимка, с целью внесения поправок за элементы ориентирования и рельеф. Каждый тип снимка (центральный, панорамный и щелевой) обрабатывается по своим матема-тическим законам. Затем снимки обрабатываются по предлагаемой методике. При корректно выбранных точках в полосе перекрытия полностью устраняются сдвиги на границе смежных снимков.

С авторами можно связаться по e-mail: panorama@gisinfo.ru

Литература:

[1] Диаграмма Вороного и триангуляция Делоне О.Р. Мусин (МГУ) Информацион-ный бюллетень ГИС-Ассоциации №2(19) 1999г сс. 51-52.
[2] От триангуляции Делоне к управляемой триангуляции (о настоящих моделях рельефа в ГИС) В.М. Огарков (АО "Аркада") Информационный бюллетень ГИС-Ассоциации №2(19) 1999г сс. 53-54.
[3] Аналитическая фотограмметрия А.Н.Лобанов "Недра" 1972г. 224с.
[4] Matrix Computations. Gene N/ Golub, Charles F. Van Loan, The Jhon Hopkins University Press Baltimor and London 1989
[5] Вычислительная геометрия и компьютерная графика на С++ Майкл Ласло "Би-ном" 1997г. 300с.