Об учете систематических искажений неметрических снимков
В.И. Юрченко
Источник: В.И. Юрченко // Геодезия и картография. - 2002. - N7. - С. 31-38
Владислав Иванович Юрченко, инженер Сибирского научно-исследовательского и производственного центра геоинформации и прикладной геодезии (Сибгеоинформ)
В области прикладной фотограмметрии актуальной задачей является разработка технологий, позволяющих оперативно и с требуемой точностью получать интересующие заказчика сведения об объектах, процессах, явлениях. Анализ состояния съемочной техники и фотограмметрических методов обработки снимков позволяет сделать вывод, что подобные технологии должны основываться на использовании мало- и среднеформатных неметрических камер, которые имеют ряд преимуществ. Это: общедоступность, сравнительно низкая стоимость, малая масса, простота в управлении, наличие вспомогательного оборудования и сменных объективов, хорошая разрешающая способность и широкий диапазон фокусирования. По ряду характеристик к классу неметрических можно отнести и широко распространенные в последнее время различные цифровые фото- и видеокамеры, которые, быстро совершенствуясь, теснят традиционную фотоаппаратуру. Отличительной особенностью таких камер является возможность получения фотографической информации сразу в цифровом виде с последующей фотограмметрической обработкой ее на персональной ЭВМ.
Но несмотря на все эти преимущества, неметрические камеры практически не используются там, где требования к точности определения геометрических характеристик объекта достаточно высоки (например, при исследовании конструкций и определении деформаций сооружений, изучении скульптур и памятников архитектуры, испытании на моделях и др). В этих случаях фотографирование объекта с близких отстояний и классические методы фотограмметрии не решают проблемы. Возникает необходимость разработки специальных приемов и методов обработки, учитывающих особенности неметрических снимков. Так, все аналитические способы обработки в обязательном порядке должны учитывать два основных фактора, определяющих точность решения задачи:
элементы внутреннего ориентирования неметрических камер (
f, x0, y0) являются переменными величинами; их колебание возникает в момент экспонирования (ввиду нежесткого крепления объектива к корпусу камеры), при перефокусировке объектива на конкретное отстояние, изменении климатических условии во время съемки и составляет: 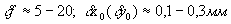 [5, 7].
[5, 7].
суммарные систематические искажения координат точек неметрических снимков имеют нелинейный и несимметричный характер и достигают на краях кадра
 0,8—0,9 мм. С учетом погрешностей, вносимых объективом, суммарные систематические искажения могут увеличиваться или уменьшаться в зависимости от изменяющегося по полю изображения знака дисторсии, т. е. имеет место перераспределение систематических искажений от кадра к кадру. Стабильным можно считать поле искажений только одиночного неметрического снимка.
0,8—0,9 мм. С учетом погрешностей, вносимых объективом, суммарные систематические искажения могут увеличиваться или уменьшаться в зависимости от изменяющегося по полю изображения знака дисторсии, т. е. имеет место перераспределение систематических искажений от кадра к кадру. Стабильным можно считать поле искажений только одиночного неметрического снимка.
Из изложенного ясно, что даже определенные в результате калибровки неметрической камеры элементы внутреннего ориентирования и параметры, учитывающие суммарное влияние всех источников систематических искажений, не будут соответствовать реально существующим в момент съемки. Следовательно, с учетом сказанного в ходе решения производственных задач по неметрическим снимкам необходимо определять как основные неизвестные (пространственные координаты точек объекта и элементы внешнего ориентирования снимков), так и дополнительные — параметры самокалибровки снимков (элементы внутреннего ориентирования и поправки за суммарные систематические искажения).
Анализу существующих методов учета систематических искажений неметрических снимков в ходе решения производственных задач с самокалибровкой, а также изложению возможного пути решения задачи самокалибровки неметрических снимков посвящена данная статья.
Как известно, существуют два основных метода учета систематических искажений снимков: полиномный и зонный [2, 4]. Теоретические основы и особенности их реализации при калибровке и самокалнбровке снимков подробно описаны в литературе и в пояснениях не
нуждаются. Рассмотрим их особенности при обработке неметрических снимков.
Полиномный метод в той или иной форме является наиболее распространенным
[1, 3, 7]. Однако в большинстве случаев математические функции
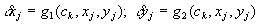
не раскрывают внутренние физические или механические источники систематических искажений, а лишь отражают их общий, суммарный характер. Практически невозможно точно установить вид и число членов интерполяционной функции, соответствующей реальным, чаще несимметричным, искажениям неметрических снимков. При неверно подобранной математической модели погрешности измерений координат точек снимка лишь усилят искажение результатов обработки. Кроме перечисленных особенностей полиномный метод требует наличия координат главной
точки (x0, y0) каждого неметрического снимка.
Зонный метод в известном варианте [4] предполагает определение поправок за систематические искажения
 для точек, расположенных в одних и тех же зонах соседних снимков. При этом число зон определения поправок и их расположение должны соответствовать стандартному расположению точек фотограмметрической сети. Поправки для изображений точек, расположенных вне этих зон, определяются путем интерполирования. Однако такая реализация зонного метода не учитывает не только сложный характер распределения систематических искажений неметрических снимков, но и возможное их перераспределение для соседних экспозиций. Отметим, что для снимков, полученных неметрическими камерами, проблематично добиться точного совпадения одноименных зон на соседних снимках, так как границы кадра могут быть плохо опознаваемы либо отсутствовать (например, на архивных снимках). Однако несмотря на существенные недостатки, зонный метод имеет преимущество перед полиномным: он позволяет лучше учитывать несимметричные и локальные искажения по всему полю изображения и при некоторой модификации может найти применение при самокалибровке неметрических снимков.
для точек, расположенных в одних и тех же зонах соседних снимков. При этом число зон определения поправок и их расположение должны соответствовать стандартному расположению точек фотограмметрической сети. Поправки для изображений точек, расположенных вне этих зон, определяются путем интерполирования. Однако такая реализация зонного метода не учитывает не только сложный характер распределения систематических искажений неметрических снимков, но и возможное их перераспределение для соседних экспозиций. Отметим, что для снимков, полученных неметрическими камерами, проблематично добиться точного совпадения одноименных зон на соседних снимках, так как границы кадра могут быть плохо опознаваемы либо отсутствовать (например, на архивных снимках). Однако несмотря на существенные недостатки, зонный метод имеет преимущество перед полиномным: он позволяет лучше учитывать несимметричные и локальные искажения по всему полю изображения и при некоторой модификации может найти применение при самокалибровке неметрических снимков.
Анализ литературы показывает, что решение задачи калибровки и самокалибровки неметрических снимков возможно также на основе метода конечных элементов
[6]. Он предполагает в данном случае деление снимка на конечные элементы (зоны), в пределах которых систематические искажения описываются аппроксимирующей функцией, имеющей непрерывные производные при переходе через границы зон. При этом форма зон зависит от вида выбранной функции. Это могут быть, кусочные, линейные, билинейные, биквадратные, сплайновые или другие функции, коэффициенты которых определяются в узловых точках зоны. Метод конечных элементов не требует наличия координат главной точки снимка. однако при обработке неметрических снимков сохраняет некоторые недостатки, присущие как зонному, так и полиномному методу. Теоретические и практические аспекты использования метода конечных элементов при калибровке топографических снимков приведены в работе [10].
Отметим, что независимо от выбранного способа учета систематических искажений определение дополнительных параметров самокалибровки снимков (тем более каждого) существенно увеличивает общее число неизвестных, что при уравнивании способствует накоплению ошибок округлений. Неверно же подобранная модель учета искажений ведет к ухудшению обусловленности исходной матрицы уравнений и не повышает точность решения задачи. Так, например, использование известных уравнений компланарности или коллинеарности, изначально требующих определения шести элементов внешнего и трех элементов внутреннего ориентирования снимка, при обработке неметрических снимков с самокалибровкой вряд ли будет эффективно.
Иным подходом к решению поставленной задачи может быть разработка способа обработки неметрических снимков при сокращенном числе дополнительных неизвестных — части элементов внутреннего и внешнего ориентирования снимка.
В работах
[8. 9] рассмотрен принципиально новый способ обработки снимков с самокалибровкой, не требующий наличия или определения координат главной точки и угла разворота к снимка. Основное уравнение в этом способе имеет вид:
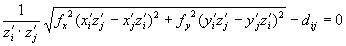 , (1)
, (1)
где
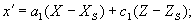



dij
— расстояние между i-й и j-й точками на снимке; Xi, Yi, Zi, Xj, Yj, Zj — пространственные координаты i-й и j-и точек объекта в заданной системе координат; XS, YS, ZS — пространственные координаты центра фотографирования;  — продольный и поперечный углы наклона снимка; fx, fy — фокусное расстояние снимка по двум взаимно перпендикулярным осям.
— продольный и поперечный углы наклона снимка; fx, fy — фокусное расстояние снимка по двум взаимно перпендикулярным осям.
Уравнение (1) содержит пять элементов внешнего ориентирования снимка —
 , XS, YS, ZS и теоретически позволяет проводить измерения снимков, не “привязываясь” к какой-либо плоской системе координат снимка или измерительного прибора. Однако ввиду отсутствия на сегодняшний день технических или программных средств, позволяющих автоматизировать процесс измерения отрезков на снимке, способом предусмотрено использование в правой части уравнения (1) вычисленных расстоянии dвыч по измеренным координатам точек снимка в произвольно выбранной плоской системе координат. Возникает необходимость учета систематических искажений снимков на основе уравнения (1).
, XS, YS, ZS и теоретически позволяет проводить измерения снимков, не “привязываясь” к какой-либо плоской системе координат снимка или измерительного прибора. Однако ввиду отсутствия на сегодняшний день технических или программных средств, позволяющих автоматизировать процесс измерения отрезков на снимке, способом предусмотрено использование в правой части уравнения (1) вычисленных расстоянии dвыч по измеренным координатам точек снимка в произвольно выбранной плоской системе координат. Возникает необходимость учета систематических искажений снимков на основе уравнения (1).
При обработке неметрических снимков предлагается использовать общий метод учета систематических искажений. позволяющий обходиться без координат главной точки снимка и получивший название метода “независимых зон”. Основные положения его следующие.
1. Область учета систематических искажений на снимке задается не углами кадрирующей рамки, а соответствует фактической области измерений снимка, которая разбивается на зоны одинаковой формы и равных размеров.
2. Поправки за систематические искажения 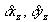 являются независимыми для одноименных зон соседних снимков и определяются одновременно по всей области измерений для каждого снимка.
являются независимыми для одноименных зон соседних снимков и определяются одновременно по всей области измерений для каждого снимка.
3. Поправки в пределах каждой зоны могут быть постоянными для всех точек, принадлежащих зоне, либо аппроксимироваться кусочной функциональной зависимостью, имеющей непрерывные производные на границах зон. В первом случае предполагается, что систематические искажения в пределах зоны имеют постоянный (линейный) характер распределения и при переходе к соседней зоне изменяются скачкообразно. Во втором — искажения в пределах зоны носят непостоянный (линейный или нелинейный) характер распределения и на границах смежных зон принимаются равными.
4. Число и форма зон, вид кусочной функции устанавливаются индивидуально для каждой снимка, исходя из сведений о характере распределения и величинах систематических искажений, точности измерений на снимках, числе опорных и определяемых точек объекта.
Таким образом, метод “независимых зон” является своеобразным синтезом полиномного и зонного методов и, сохраняя основные преимущества обоих, позволяет учитывать систематические искажения только области измерений каждого включенного в обработку снимка. При этом изменением числа и формы зон, видом кусочной функции учитывается практически любой характер распределения систематических искажений снимка. Основным условием, определяющим точность и достоверность результатов самокалибровки на основе метода “независимых зон”, является достаточное для нахождения однозначного решения задачи число и равномерное распределение измеренных точек в зонах, что обычно не вызывает затруднений при решении задач фотограмметрии близких отстояний. С точки зрения построения и уравнивания сети фототриангуляции связанная и переопределенная система уравнений может быть получена за счет измерений одноименных точек объекта, расположенных в различных частях нескольких снимков.
Для разработки модели учета систематических искажений при отсутствии координат главной точки снимка за основу было принято допущение, согласно которому все искажения, существующие в плоскости изображения, описываются изменением масштаба снимка, который, в свою очередь, является функцией фокусного расстояния снимка
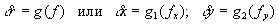
Тогда отклонение
j-й точки изображения от ее истинного положения будет соответствовать изменению фокусного расстояния снимка в данной точке

Применительно к методу “независимых зон” учет систематических искажений точек в пределах
z-й зоны снимка соответствует определению фокусного расстояния снимка в этой зоне fz или fxz, fyz. В свою очередь, фокусное расстояние z-й зоны может быть постоянной в ее пределах величиной fz = const (или описываться кусочной аппроксимирующей функцией fz =  с определением значений fjz в узловых точках зоны.
с определением значений fjz в узловых точках зоны.
Таким образом, использование в качестве параметров самокалибровки переменного числа фокусного расстояния
каждого снимка позволит в ходе решения производственной задачи одновременно учитывать как систематические искажения, вызывающие смещение точек снимка по радиальным и тангенциальным направлениям (дисторсия объектива, отклонение плоскости изображения от фокальной плоскости объектива, деформация фотоматериала и др.), так и колебания фокусного расстояния камеры во время съемки. В работах: [8, 9] подтверждена работоспособность способа обработки, в котором учет систематических искажений неметрических снимков в ходе самокалибровки проводился путем определения для каждого снимка фокусных расстояний fx и fy как по двум взаимно перпендикулярным направлениям, так я по зонам.
В данной работе предлагается классификация возможных математических моделей учета систематических искажений снимков, разработанных на основе метода “независимых зон”, где в качестве параметров самокалибровки принимаются переменные значения фокусного расстояния каждого снимка (см. рисунок). Отличительной особенностью всех моделей является учет систематических искажений при отсутствии координат главной точки снимка.
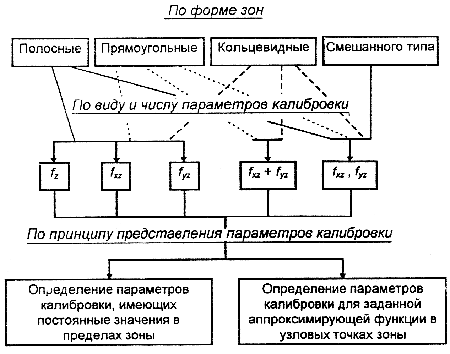
Рисунок. Классификация математических моделей учета систематических искажений снимков на основе метода “независимых” зон
Дадим некоторые пояснения приведенной на рисунке классификации. Так, классификация предусматривает при разработке моделей использование зон различной формы: полосных, прямоугольных, кольцевидных и смешанного типа. Полосные зоны подразумевают деление области измерений на полосы, параллельные осям
x или y, для произвольно выбранной плоской системы координат снимка. При этом ширина полос может быть различна по осям. Прямоугольные зоны со сторонами a и b соответствуют форме, установленной для зонного метода [4]. Кольцевидные зоны шириной d=Rz+1-Rz, где Rz — радиус z-й зоны снимка, представляют собой зоны радиально-кольцевидного типа, центром которых является центр тяжести измеренных точек снимка. Отметим, что возможно использование иной, отличной от классификации формы, которая определяется исходя из характера систематических искажении снимка.
Различие моделей но виду и числу параметров калибровки предусматривает определение в
z-й зоне снимка одного (fz, fxz, fyz) или одновременно двух параметров калибровки (fxz + fyz). Кроме того, возможен вариант, когда каждый из двух параметров (fxz и fyw) определяется для своего числа и размеров зон: fxz для z-й зоны по оси x, fyw для w-й зоны по оси y. Для данного варианта предусмотрена возможность использования зон смешанного типа: полосно-прямоугольных, полосно-кольцевых, прямоугольно-кольцевых, позволяющих определять каждый параметр калибровки для зон своей формы (например, параметр fxz определяется для полосных, а fyw —для прямоугольных зон).
Различие моделей по принципу представления параметров калибровки предусматривает возможность как определения параметра (или параметров) калибровки, имеющего постоянное и единственное в пределах зоны значение (например,
f=const), так и определение в зоне нескольких параметров калибровки одного вида. Во втором случае необходимо задать кусочную аппроксимирующую функцию, имеющую непрерывные производные при переходе через границы зоны. Значения выбранной функции определяются в узловых точках или на структурных линиях зон, где число узловых точек зависит от вида функции. Определение значений функции в узловых точках соответствует использованию зон трех- или четырехугольной формы (двумерный случай), а на структурных линиях — зон полосной или кольцевидной формы (одномерный случай).
Предложенная классификация позволяет разрабатывать индивидуальную модель снимка, учитывающую систематические искажения изображений, полученных неметрическими камерами любого типа, включая цифровые фото- и видеокамеры.
При использовании математических моделей, разработанных на основе метода “независимых зон”, возникает вопрос о выборе необходимого их числа и размеров для определения дополнительных параметров самокалибровки снимков. Известно, что точность решения задачи самокалибровки зависит не только от степени учета систематических искажений снимков, но и от вида г. числа опорных данных, расположения точек на снимке, общей геометрии сети. Так, например, правильно подобранная математическая модель учета систематических искажений может не обеспечить получение результатов необходимой точности при недостаточном числе опорных данных или геометрически некорректном расположении точек на снимке. Необходим комплексный учет всех перечисленных факторов, т. е. возникает потребность в автоматическом выборе вида и числа дополнительных параметров самокалибровки с учетом индивидуальных особенностей сети.
В работе [9] автором предложена процедура двухступенчатой автоматической оптимизации, позволяющая установить число зон определения параметров самокалибровки каждого снимка. В качестве функций оптимизации приняты след
Sp(K) и число обусловленности COND(K) ковариационной матрицы K. В ходе оптимизации выполняется многократное решение задачи по определению пяти элементов внешнего ориентирования ( , XS, YS, ZS ) и переменного числа параметров самокалибровки каждого снимка с последующим статистическим оцениванием уравненных параметров. Решение задачи выполняется по всем точкам, принадлежащим снимку, и в соответствии со схемой формирования уравнений поправок, используемой при дальнейшем строгом уравнивании. Число вариантов решения зависит от заданного пользователем максимально возможного числа зон снимка.
, XS, YS, ZS ) и переменного числа параметров самокалибровки каждого снимка с последующим статистическим оцениванием уравненных параметров. Решение задачи выполняется по всем точкам, принадлежащим снимку, и в соответствии со схемой формирования уравнений поправок, используемой при дальнейшем строгом уравнивании. Число вариантов решения зависит от заданного пользователем максимально возможного числа зон снимка.
После расчета всех вариантов решение проводится первый этап оптимизации, предназначенный для отбраковки наиболее грубых вариантов. Используя функцию оптимизации
Sp(K) на основе статистического критерия проверяют гипотезу H0 о равноточности различных вариантов решения для установленного 3%-ного уровня значимости 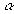 . На втором этапе проводится выбор единственного варианта решения, имеющего наименьшее значение числа обусловленности ковариационной матрицы COND(K) = min. Однако, как показывает опыт, более достоверным является использование на втором этапе функции вида
. На втором этапе проводится выбор единственного варианта решения, имеющего наименьшее значение числа обусловленности ковариационной матрицы COND(K) = min. Однако, как показывает опыт, более достоверным является использование на втором этапе функции вида
 (2)
(2)
где
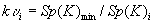 — выравнивающий коэффициент;
— выравнивающий коэффициент;  — наименьшее значение следа ковариационной матрицы, выбранное из всех оставшихся после первого этапа вариантов решения задачи;
— наименьшее значение следа ковариационной матрицы, выбранное из всех оставшихся после первого этапа вариантов решения задачи;  — след ковариационной матрицы i-го варианта решения задачи.
— след ковариационной матрицы i-го варианта решения задачи.
На основе вычислений по формуле (2) принимается решение о числе и размерах зон определения дополнительных параметров самокалибровки для каждого снимка. Дальнейшее строгое уравнивание проводится для выбранного процедурой числа параметров самокалибровки.
Отметим, что отличия условий решения задачи в процедуре оптимизации от условий строгого уравнивания (определение лишь неизвестных, относящихся к снимку, влияние точности приближенных значений пространственных координат точек объекта) приводят к тому, что выбранное число зон на снимке не всегда оптимально. С целью устранения этого несоответствия алгоритмом предусмотрено предварительное уравнивание неизвестных, заключающееся в поэтапном решении прямой (обратной) фотограмметрической засечки по всем измеренным точкам снимков. Таким образом, разработанная на основе приведенных выше теоретических положении процедура позволяет при дальнейшем уравнивании неизвестных получать оптимальное для данных условии математическое решение задачи. Приведенные в работах
[8, 9] результаты обработки неметрических снимков свидетельствуют о том, что разработанный на основе уравнения (1) аналитический способ, включающий процедуру оптимизации числа параметров самокалибровки, по точности обеспечивает решение многих задач прикладной фотограмметрии.
В заключение следует сказать, что в дальнейшем предполагается расширить теоретическую базу разработанного метода учета систематических искажении снимков за счет реализации иных принципов представления параметров калибровки. Кроме того, автор не исключает возможности использования метода при обработке снимков иной геометрии формирования изображения — сканерных, щелевых, панорамных.
Практическому исследованию метода “независимых зон” с точки зрения полноты учета систематических искажений неметрических снимков будет посвящена отдельная статья.
Список литературы
1.Амромин П.Д. Обработка неметрических снимков фотограмметрическими методами отстояний // Геодезия и картография. – 1995 - №9. – С. 27-30
2.Аналитическая пространственная фототриангуляция / А.Н. Лобанов, В.Б. Дубиновский, М.М. Машимов, Р.П. Овсянникво – М.: Недра, 1991. – 255с.
3.Гельман Р.Н., Никитин М.Ю., Никитин А.В. Об учете дисторсии при обработке видеоизображений отстояний // Геодезия и картография. – 2000 - №11. – С. 19-22
4.Дубиновский В.Б. Калибровка снимков. – М.: Недра, 1982, - 224с.
5.Катушников В.А. Исследования и анализ отклонений главной точки снимка при фокусировании объектива камеры // Изв. вузов. Сер. Геодезия и аэрофотосъемка. – 1991. –
N2. – С. 89-94
6.Метод конечных элементов: Основы. – Пер. с англ. – М.: Мир, 1984. – 428с.
7.Сердюков В.М., Катушков В.А., Садовец Б.А. Опыт применения неметрических фотокамер при съемке с близких отстояний // Геодезия и картография. – 1988 - №9. – С. 27-30.
8.Юрченко В.И. Способ аналитической обработки неметрических снимков // Геодезия и картография. – 2000 - №11. – С. 23-30.
9.Юрченко В.И. Усовершенствование способа аналитической обработки неметрических снимков // Геодезия и картография. – 2001 - №1. – С. 33-36.
10.Munjy R.A. H. Self-calibration using the finite element approach //Photogrammetric engineering and remote sensing. – 1986. – Vol. 52, N3. – P. 411-418.

