














Разработка Модели и Оптимизация параметров компьютерных систем предприятий Айман Абделькарим
Домой СОДЕРЖАНИЕ Заключение Введение
Анализ
1. АНАЛИЗ СРЕДСТВ ПРЕДСТАВЛЕНИЯ И ВЫБОР МЕТОДОВ ИССЛЕДОВАНИЯ СТРУКТУР ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ
Выбор методов,
используемых в теории ВС, предопределяется
характером процессов в ВС и целями, которые
ставятся при проведении исследований.
Вероятностный подход к исследованию ВС [1]. Процесс функционирования ВС — это процесс выполнения совокупностью устройств некоторого набора программ (алгоритмов). В теории ВС вычислительные процессы в системах изучаются в основном во временном аспекте— с целью определения временных характеристик процесса функционирования систем:
v доли времени, в течение которого устройства простаивают;
v времени получения каких-то результатов, производимых соответствующей программой;
v производительности, определяемой числом задач, решаемых в единицу времени, и т. п.
Для ВС типично наличие элемента случайности в порядке инициирования программ, реализуемых системой [2]. Так, во-первых, запросы на выполнение программ генерируются пользователями в случайные моменты времени; пакет программ, предназначенных для обработки, состоит из случайным образом сформированной смеси задач и т. д. Во-вторых, хотя процесс выполнения программы по своей сути детерминированный, однако практическая бесконечность числа различных вычислительных процессов, порождаемых программой в зависимости от исходных данных, не позволяет выявить представляющие интерес свойства вычислительных процессов при исследовании их с позиций детерминизма.
Многочисленность вариантов выполнения программы является фактором, предопределяющим необходимость исследования вычислительного процесса как процесса случайного. Такой подход правомочен тогда, когда свойства изучаемого объекта проявляются на множестве процессов, например, на множестве реализаций программы или совокупности программ. Таким образом, случайный характер инициирования программ, практическая непредсказуемость данных, обрабатываемых программой, и связанная с этим случайность моментов времени, в которые начинает выполняться и заканчивается программа, приводят к необходимости рассматривать процесс функционирования ВС как случайный процесс и изучать свойства ВС с позиций теории вероятностей. В связи с этим алгоритмы, несмотря на присущую им определенность, интерпретируются как генераторы случайных процессов, порождающие в случайные моменты времени запросы на передачу и обработку информации, и фактор случайности включается в модели алгоритмов.
Итак, функционирование ВС можно рассматривать как композицию трех классов в общем случае недетерминированных процессов:
1) на входе ВС, порождающих заявки на выполнение определенных алгоритмов (программ);
2) выполнения программ, порождающих заявки на передачу и обработку информации;
3) обслуживания заявок устройствами, обеспечивающими передачу и обработку информации.
Изучение процессов, связанных с обслуживанием какого-либо вида запросов, с учетом случайного характера поступления запросов и обслуживания проводится в рамках теории массового обслуживания, являющейся разделом прикладной математики. Аппарат теории массового обслуживания — основной в теории ВС, широко используемый для постановки и решения задач анализа ВС.
Большинство моделей теории ВС строится на основе моделей теории массового обслуживания. В теории массового обслуживания изучаются процессы, являющиеся в основном марковскими либо некоторым образом связанные с марковскими процессами. Поэтому для решения задач теории массового обслуживания используется аппарат теории марковских процессов.
В теории ВС применяют аналитические, числовые и экспериментальные методы исследования.
Аналитические методы [3]. Аналитические методы состоят в преобразовании символьной информации, записанной на языке математического анализа. При использовании аналитических методов строится математическая модель объекта, представляющая физические свойства объекта в виде математических объектов и отношений (математических операций над величинами), например в виде дифференциальных или интегральных уравнений. Математическая модель строится на основе понятий, символики и методов некоторой теории, например теории массового обслуживания, определяющей класс математических аналогий, т. е. основополагающих математических моделей. При аналитическом подходе требуемые зависимости выводятся из математической модели последовательным применением математических правил. Препятствием при этом может быть неразрешимость уравнений в аналитической форме, отсутствие первообразных для подынтегральных функций и т. п., с чем приходится сталкиваться весьма часто. Поэтому лишь при определенных свойствах модели можно получить решение в явной аналитической форме. Несмотря на ограниченные возможности аналитического подхода, решения, полученные в явной аналитической форме, имеют большую познавательную ценность и находят результативное применение при решении широкого класса теоретических и прикладных задач.
Численные методы [2]. Численные методы основываются на построении конечной последовательности действий над числами, приводящей к получению требуемых результатов. При наличии математической модели исследуемого объекта применение численных методов сводится к замене математических операций и отношений соответствующими операциями над числами: замене интегралов- суммами, производных разностными отношениями, бесконечных сумм конечными и т. д. В результате этого строится Алгоритм, позволяющий точно или с допустимой погрешностью определить значения требуемых величин. Алгоритм реализуется вручную или программируется для ЭВМ. Результат применения численных методов — таблицы (графики) зависимостей, раскрывающих свойства объекта. Численные методы по сравнению с аналитическими позволяют решать значительно более широкий круг задач.
Характер процессов, присущих исследуемому объекту и подлежащих отображению в модели, может быть столь сложным, что построение математической модели превращается в трудную задачу, а анализ модели даже численными методами может оказаться нерезультативным из-за трудоемкости или неустойчивости алгоритмов в отношении погрешностей аппроксимации и округления. Воспроизведение в модели динамики сложных пространственно-временных отношений между объектами, образующими систему, всего многообразия ее связей со средой, действующих в системе законов управления, адаптивных свойств и черт целенаправленного поведения трудновыполнимо чисто математическими средствами. При исследовании таких систем широкое применение находят модели, представляющие собой содержательное описание объектов исследования в форме алгоритмов. В описаниях отражаются как структура исследуемых систем, что достигается отождествлением элементов систем с соответствующими элементами алгоритмов, так и процессы функционирования систем во времени, представляемые в логико-математической форме [6]. При этом описания объектов исследования имеют алгоритмический характер, а сами модели суть программы для ЭВМ. Модели такого типа называют имитационными или алгоритмическими.
Главная особенность данного подхода к моделированию заключается в том, что используемые для построения модели алгоритмические языки — гораздо более гибкое и доступное средство описания сложных систем, нежели язык математических функциональных соотношений: Благодаря этому в имитационных моделях сложных систем находят отражение многие детали их структуры и функций, которые вынужденно опускаются или непроизвольно утрачиваются в математически строгих моделях. Свойственная имитационным моделям реалистичность основывается на использовании для их построения всех имеющихся представлений об объекте исследования как теоретического, так и эвристического характера.
В теории ВС с присущим ей вероятностным подходом к анализу систем при построении имитационных моделей наиболее {широко используется метод статистических испытаний (метод Монте-Карло) [7]. Процедура построения и анализа имитационных моделей методом статистических испытаний называется статистическим моделированием. Статистическое моделирование представляет собой процесс получения статистических данных о процессах, происходящих в моделируемой системе. Для получения представляющих интерес результатов статистические данные обрабатываются и классифицируются с использованием методов математической статистики. Позитивное свойство статистического моделирования — универсальность, гарантирующая принципиальную возможность анализа систем любой степени сложности с любой степенью детализации изучаемых процессов. Негативное свойство статистического моделирования—трудоемкость процесса .моделирования, т. е. необходимость выполнения очень большого количества операций над числами, и частный характер результатов, не раскрывающий зависимости, а лишь определяющий ее в отдельных априорно назначенных точках.
Экспериментальные методы [18]. Экспериментальные методы базируются на измерении характеристик вычислительных процессов, происходящих в реальных системах, и обработке результатов измерения с целью выявления представляющих интерес зависимостей. Экспериментальные исследования являются источником наиболее достоверной информации, однако получаемые при этом результаты носят частный характер. Эти методы — пока единственный источник сведений о характеристиках задач, решаемых в вычислительных центрах, процессах взаимодействия пользователей с ВС и 'г. д. Данные сведения используются в качестве исходных данных при проектировании новых ВС. Естественно, что возможности экспериментальных методов ограничиваются парком существующих ВС.
При проведении исследований даже узкого круга вопросов возникает необходимость в использовании нескольких методов решения одной и той же задачи. Решение' задач аналитическими методами всегда предполагает использование допущений, принимаемых либо на этапе построения концептуальной модели, либо на этапе построения математической модели, т. е. вывода результирующих зависимостей. Получаемые при этом зависимости могут быть использованы для решения прикладных задач только после оценки методической погрешности, вносимой принятыми допущениями. Оценить погрешность аналитическими методами — задача обычно более сложная, чем вывод зависимостей. Поэтому для оценки методической погрешности -широко используется метод имитационного моделирования, позволяющий получить численное решение с любой заданной точностью. В таком же аспекте используются и экспериментальные методы анализа ВС.
Методы оптимизации. Задачи синтеза ВС решаются с использованием численных методов оптимизации, иначе называемых методами математического программирования. Методология постановки и решения экстремальных задач на основе математических и имитационных моделей систем изучается в общей постановке в рамках исследования операций [5].
1.1 Обзор математических моделей, используемых при исследованиях вычислительных систем
Вычислительные системы относятся к структурам преемлющим методы операционного исследования или математического моделирования [1]. Впервые математические модели были использованы для решения практической задачи в 30-х годах в Великобритании при создании системы управления противовоздушной обороной. Для разработки данной системы были привлечены ученые различных специальностей. Система создавалась в условиях неопределенности относительно возможных действий противника, поэтому исследования проводились на адекватных математических моделях. В то время впервые был применен термин: «операционное исследование», подразумевавший исследования военной операции. В последующие годы операционные исследования или исследования операций развиваются как наука, результаты которой применяются для выбора оптимальных решений при управлении реальными процессами и системами.
Можно выделить следующие основные этапы операционного исследования:
1) наблюдение явления и сбор исходных данных;
2) постановка задачи;
3) построение математической модели;
4) расчет модели;
5) тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует либо вернуться на этап 3, т.е. предложить для решения задачи другую математическую модель; либо вернуться на этап 2, т.е. поставить задачу более конкретно;
6) применение результатов исследований.
Таким образом, операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчет математической модели.
Математическая модель – это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему.
Проведение операционного исследования, построение и расчет математической модели позволяют проанализировать ситуацию и выбрать оптимальные решения по управлению или обосновать предложенные решения. Применение математических моделей необходимо в тех случаях, когда проблема сложна, зависит от большого числа факторов, по-разному влияющих на ее решение, что мы имеем при исследовании вычислительных систем, являющихся типичными представителями многофакторных объектов. В этом случае непродуманное и научно не обоснованное решение может привести к серьезным последствиям, например к сбоям в работе отдельных компонент вычислительной системы при неурегулированных на этапе разработки и внедрения режимах использования мультидоступных ресурсов.
Использование математических моделей позволяет осуществить предварительный выбор оптимальных или близких к ним вариантов решений по определенным критериям. Они должны быть научно обоснованы, и лицо, принимающее решения, может руководствоваться ими при выборе окончательного решения. Следует понимать, что не существует решений, оптимальных «вообще». Любое решение, полученное при расчете математической модели, оптимально по одному или нескольким критериям, предложенным постановщиком задачи и исследователем.
В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений в различных областях науки и техники. Это планирование и оперативное управление производством, управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, анализ и синтез структур вычислительных систем.
Рассмотрим классификацию и принципы построения математических моделей. Можно выделить следующие основные этапы построения математической модели.
1. Определение цели, т.е. чего хотят добиться, решая поставленную задачу.
2. Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
3. Формирование управляющих переменных, изменяя значения которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.
4. Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
5. Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.
6. Выражение цели через управляющие переменные, параметры и неизвестные фактор, т.е. формирование целевой функции, называемой также критерием оптимальности задачи.
Введем следующие условные обозначения:
α – параметры модели;
x – управляющие переменные или решения;
X – область допустимых решений;
ξ – случайные или неопределенные факторы;
W – целевая функция или критерий эффективности (критерий оптимальности).
Решить задачу – это значит найти такое оптимальное решение x* Î X, чтобы при данных фиксированных параметрах α и с учетом неизвестных факторов ξ значение критерия эффективности W было по возможности максимальным (минимальным).Таким образом, оптимальное решение — это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким).
В данной работе необходимо построить модель вычислительной системы, α – параметры которой есть характеристики выполняемых компьютерных программ; в качестве x – управляющих переменных или решений выступает топология сети; X – область допустимых структурных решений; ξ – случайные или неопределенные факторы; W – целевая функция или критерий эффективности. Как правило, такой критерий - минимальная стоимость при заданном времени решения задач.
Перечислим некоторые основные принципы построения подобной математической модели[1].
1. Необходимо соизмерять точность и подробность модели, во-первых, с точностью тех исходных данных, которыми располагает исследователь, и во-вторых, с теми результатами, которые требуется получить.
2. Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.
3. Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.
4. Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.
Учитывая многокомпонентность вычислительных систем, необходимость представления в дальнейших исследованиях как процессов так и структур, рассмотрим существующую классификация математических моделей, которая представлена на рис.1.
По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В стохастических моделях неизвестные факторы — это случайные величины, для которых известны функции распределения. И различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т. п.). Среди стохастических можно выделить:
v модели стохастического программирования, в которых либо в целевую функцию (1.1), либо в ограничения (1.2) входят случайные величины;
v модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной. Таковыми являются многопользовательские ресурсы вычислительных систем.
v модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений, а также модели вычислительных систем.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности. В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например организацию предприятия в условиях конкуренции.
В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействий на него, например организация производственного процесса или организация вычислительного процесса в проектируемой вычислительной системе. Имитация на проектном этапе позволяет выяснить правильность прогнозных расчетов.
Предполагается, что в данной работе будут использоваться только детерминированные модели. В детерминированных моделях неизвестные факторы не учитываются.
По виду целевой функции и ограничений детерминированные модели делятся на линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения, что и предпринято в данной работе.
Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения.















![]()
![]()
![]()
![]()
![]()
Рис. 1 Классификация математических моделей
Нелинейные модели — это модели, в которых либо целевая функция, либо
какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений используются различные способы решения. Однако может случиться и так, что для поставленной нелинейной задачи вообще не существует метода расчета. Поэтому в данной работе задачи предполагается упрощать, либо сводить ее к известным линейным моделям, а, чаще, просто линеаризовать модель.
В динамических моделях в отличие от статических линейных и нелинейных моделей учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения. Динамические модели планируется применить на этапе оценки экономической эффективности при моделировании динамики финансовых потоков.
Графические модели используются тогда, когда задачу удобно представить в виде графической структуры, ориентированным взвешенным графом. Например граф-схема алгоритма или граф информационной связности всего комплекса задач, решаемых в вычислительной системе, которые широко используются для решения задач расчета параметров программ, распределения потоков заявок между ресурсами вычислительной системы и т.д.
Большинство из представленных в классификации типов моделей необходимы и будут применяться на различных стадиях исследования вычислительных систем. Их выбору посвящен следующий раздел.
1.2 Выбор моделей для представления вычислительных систем и их компонент
1.2.1 Модели алгоритмов
Современная вычислительная система (ВС) представляет собой программно- технический комплекс функционирующий в интерактивном режиме. Задачи, сформулированные для ЭВМ представляются множеством исходных данных, множеством искомых результатов и программой, описывающей алгоритм решения задачи. Алгоритм - это правило, определяющее последовательность действий над исходными данными, приводящими к получению искомых результатов. Ссылки на используемые в алгоритме операнды и операции косвенно указывают на необходимые в составе ВС ресурсы.
Алгоритмы могут представляться в словесной форме с использованием необходимой математической символики (формулы), средствами некоторой алгоритмической системы - в виде:
□ логической схемы алгоритма;
□ граф-схемы алгоритма;
□ блок-схемы алгоритма;
□ матричной схемы алгоритма.
Все перечисленные формы взаимосвязаны и существуют методы для расчета на их основе характеристик алгоритмов. Основные характеристики алгоритмов:
v частота инициации (внешний, не зависящий от алгоритма параметр, характеризующийся математическим ожиданием и измеряемый в 1/с);
v перечень и порядок используемых ресурсов при однократном пуске алгоритма (вероятность и трудоемкость использования ресурсов, задаваемые матрицей вероятностей передач заявок и вектором трудоемкости их обслуживания на каждом типе ресурса).
Важнейший параметр алгоритма - трудоемкость [2]. Трудоемкость - количество вычислительой работы, требуемой для реализации алгоритма. Если сложность алгоритма характеризует потребность алгоритма в памяти, то трудоемкость — его потребность во времени, связанном с периодом работы совокупности устройств, средствами которых реализуется алгоритм. Трудоемкость алгоритма иначе называют сложностью вычислений. Оценивается трудоемкость алгоритма количеством операций, выполняемых с целью обработки, ввода и вывода информации в процессе решения задачи. Каждой реализации алгоритма присущ элемент случайности, Связанный с тем, что исходные данные представляют собой в общем случае случайную выборку из множества исходных данных, к которым применим алгоритм. Поэтому полная характеристика трудоемкости предполагает описание количества операций, выполняемых за одну реализацию алгоритма, случайными величинами, т. е. предполагает определение законов распределения числа операций в реализации алгоритма. Получение таких сведений об алгоритме — сложный и длительный процесс. В связи с этим трудоемкость алгоритмов обычно характеризуют приближенно, например, только математическими ожиданиями числа выполняемых операций.
В первом приближении трудоемкость алгоритма можно охарактеризовать следующей совокупностью параметров: θ — среднее количество процессорных операций, выполняемых за одну реализацию алгоритма (при одном прогоне программы); N1 ,…, Nн — среднее количество обращений к файлам F1, ..., Fн соответственно за одну реализацию алгоритма; 1, ...., н — среднее количество информации (байтов), передаваемое за одно обращение к файлам. Значение характеризует трудоемкость обработки информации (счета).
При решении задач анализа и синтеза ВС возникает необходимость в описании вычислительных процессов, порождаемых алгоритмами решения задач. Однако при решении задач теории ВС интерес представляют не все без исключения детали вычислительных процессов, а только те, которые характеризуют порядок использования ресурсов системы в процессе решения задач.
Количество действий, выполняемых в процессе вычислений, определяется трудоемкостью алгоритма, и если при построении модели вычислительного процесса исходить только из сведений о трудоемкости алгоритма, то степень приближения модели к реальным процессам целиком определяется полнотой и достоверностью сведений о трудоемкости алгоритма. С учетом сведений о трудоемкости алгоритма, которыми обычно располагают, и возможных подходов к анализу и синтезу ВС можно сформулировать следующие требования к моделям вычислительных процессов [16].
1. Модель должна определять порядок порождения алгоритмом запросов на каждый из видов обслуживания — счет и ввод — вывод информации, хранимой в каждом из файлов.
2. Модель должна определять трудоемкость обслуживания запросов количество операций, которое должен выполнить процессор при обслуживании запроса на счет, и количество символов водимой — выводимой информации.
3.
Модель должна отображать вычислительные процессы как
реализации случайного процесса, т. е. порождать запросы в случайные
моменты времени и характеризовать трудоемкость запросов
случайными величинами.
4.
Вычислительные процессы, порождаемые
моделью, должны
соответствовать реальным процессам с
точностью до совладения
Но крайней мере
математических ожиданий их одноименны характеристик.
Первые два требования выделяют круг сведений о вычислительных процессах, наиболее существенно влияющих на порядок функционирования ВС. На данном уровне рассмотрения вопросов. Прочие сведения о вычислительных процессах не принимаются во внимание, т. е. алгоритмы и вычислительные процессы считаются случайными постольку, поскольку они различаются по количеству И характеру запросов на обслуживание. Необходимость третьего требования продиктована результативностью вероятностного подхода к исследованию многообразных процессов, какими являются вычислительные процессы. Фактор случайности, вводимый в модель, позволяет порождать бесконечное число реализаций вычислительного процесса, что характерно для .процессов выполнения алгоритма. Последнее требование определяет минимальную норму «точности» модели. Конечно, идеальная модель должна представлять реальные процессы с точностью до равенства распределений соответствующих случайных величин, описывающих вычислительные процессы. Однако от построения идеальной модели приходится отказаться по следующим причинам. Во-первых, в подавляющем большинстве случаев сведения об алгоритмах, для выполнения которых создается система, далеко не полные. В лучшем случае известны, оценки математических ожиданий характеристик алгоритма и лишь иногда — их дисперсии. Поэтому бесполезно вводить в модель параметры, значения которых не удается определить. Во вторых, оправданное стремление получить общее решение задачи, пусть и приближенное, заставляет идеализировать вычислительные процессы — представлять их в виде, обеспечивающем разрешимость задачи аналитическими методами. Конечно, всегда должна устанавливаться степень достоверности результатов, получаемых на основе идеализированных моделей.
С учетом вышеперечисленных требований построим модель вычислительного процесса, порождаемого алгоритмом с заданной трудоемкостью.
Будем рассматривать вычислительный процесс как последовательность этапов "счета и обмена информацией файлами F1,…, FH. Типичная диаграмма такого процесса изображена на рис. 2. Состояние вычислительного процесса, соответствующее этапу счета, обозначим символом S0, а состояния, соответствующие обращениям к файлам F1,…,FН, — символами S1,…,SH. Окончание вычислительного процесса будем рассматривать как переход процесса в состояние SH+1, поглощающее вычислительный процесс. В этих обозначениях вычислительный процесс — это последовательность состояний, St0, изменяющихся в моменты времени t0, t1,…, tm, причем Sti {S0, ..., SH} и заключительное состояние процесса StM=SH+1.
Марковская модель вычислительных процессов [2]. Наиболее простую модель можно получить, если принять допущение об отсутствии последействия в вычислительном процессе, означающем, что следующее состояние вычислительного процесса зависит только от текущего состояния и не зависит от предыдущих состояний. В таком случае вычислительный процесс становится марковским процессом, определяемым множеством присущих ему состояний {S0, . . . , Sh+1}, матрицей вероятностей переходов
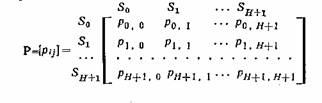
и распределением вероятностей (а0, . . . , ан+1 )состояний S0, ... , SH+1 момент времени 0. Элементы рij матрицы Р определяют вероятности перехода процесса из состояний Si в состояния Si+1 т. е. вероятности того, что процесс, находящийся в состоянии Si, в следующий момент времени будет находиться в состоянии Si+1. Матрица Р — стохастическая матрица,
построчные суммы элементов которой
Вероятности аj,; определяют первое возможное состояние St0 процесса.
Будем считать, что вычислительный процесс развивается следующим образом. Процесс начинается с состояния S0, т. е. программа начинает выполняться с этапа счета. Этап обмена может, быть инициирован только процессором, т. е. может следовать только за этапом счета. Это одновременно означает, что после каждого этапа ввода — вывода следует этап счета. В таком случае вероятности начальных состояний таковы:
![]()
а матрица вероятностей переходов имеет вид -
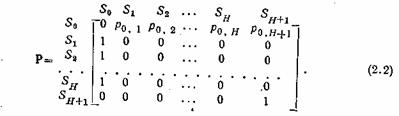
Из состояния счета S0 процесс с соответствующей вероятностью может перейти в состояния S1 , . . . , SH, представляющие этапы обращения к файлам F1,…, ,FН или в поглощающее состояние SH+1. Из состояний S1 , . . . , Sн процесс с вероятностью 1 возвращается и состояние счета S0. Достигнув поглощающего состояния Sн+1 процесс с вероятностью 1 навсегда остается в нем. Порядок смены состояний наглядно проявляется на графе марковской цепи (рис. 2). Переходы между состояниями S0, . . . , SH+1 представляются на графе дугами, на которых обозначены вероятности переходов, отличные от 1.
Значения вероятностей p0,1 ,…, p 0,H+1 предопределяют ход вычислительного процесса и зависят от параметров трудоемкости алгоритма. Эти значения вычисляются следующим образом. Трудоемкость алгоритма определяет, в частности, среднее число N1 ,…,Nн обращений к файлам F1 ,. . . , Fн. Следовательно, среднее число переходов из состояния S0 в состояния S1, . . . , Sh должно быть (N1+ . . . +NН). Один раз процесс переходит из состояния S0 в поглощающее состояние Sh+1. Таким образом, вычислительный процесс должен выходить из состояния S0 в среднем
![]() (2.3)
(2.3)
раз, т. е. в процессе реализации
алгоритма этапы счета встречаются
в среднем N раз.
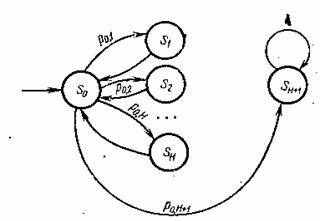
Рис. 2 Граф марковской цепи, являющейся моделью алгоритма
Количество работы, выполняемой на каждом из этапов, характеризуется параметрами 1 , . . . , н алгоритма. Значение определяет среднее количество процессорных операций, выполняемых за одну реализацию алгоритма, и значения
1, . . . ,H —среднюю трудоемкость этапов, соответствующих состояниям S1, . . . , SH.
Средняя трудоемкость этапа счета
1=N,
где N — среднее число этапов счета, определяемое Таким образом, под моделью вычислительного процесса будем понимать марковскую цепь с (H+2) состояниями, начальным состоянием S0 и матрицей вероятностей переходов (2.2). Реализация вычислительного процесса — случайная последовательность состояний S0, St1, St2, . . . , Stм, порядок смены которых определяется в вероятностном смысле матрицей вероятностей переходов. С состояниями S0, . . . , SH связано определенное количество работы, характеризуемое значениями случайных величин 0, . . . , H соответственно.
Для оценки общей трудоемкости алгоритмов используются методы теории марковских цепей. Совокупность операторов и связей между ними наиболее наглядно представляется графом алгоритма, который строится как композиция вершин, соответствующих операторам алгоритма, и дуг, отображающих связи между операторами. Выделяют вершины: начальные, конечные, операторные. Начальная вершина не имеет ни одного вход, и имеет только один выход. Такая вершина определяет начало алгоритма. Конечная вершина имеет не менее одного входа и ни одного выхода; определяет конец алгоритма. Операторная вершина соответствует основному оператору или оператору обмена данными. Вершина, представляющая функциональный оператор или оператор ввода — вывода, может иметь любое не меньшее 1 число входов и только один выход. Вершина, представляющая оператор перехода, может иметь любое не меньшее 1 число входов и не меньше двух выходов
 |
|
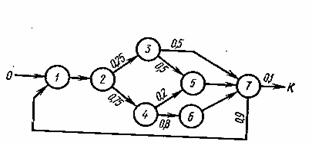
Рис. 3 Граф алгоритма, используемый при оценке трудоемкости |
В любой ситуации оператор перехода определяет один и только один выход из представляющей его вершины.
Граф алгоритма является корректным, если выполняются следующие условия:
1) имеется только одна начальная и только одна конечная вершина
2) для каждой вершины кроме начальной существует по крайней мере один путь, ведущий в эту вершину из начальной;
3) из каждой вершины кроме конечной существует по крайней мере один путь, ведущий из этой вершины в конечную;
4) выход из любой вершины должен вести только к одной вершине графа; 5) при любых значениях логических условий существует путь из начальной вершины в конечную, причем любому фиксированному набору значений условий соответствует только один такой путь.
Пример графа алгоритма приведен на рис. 3 Условимся вершины графа обозначать номерами О, 1, ..., K: 0 соответствует начальной вершине графа; K — конечной вершине; 1, . . . , K—1 идентифицируют операторы алгоритма. В программировании графы алгоритмов изображаются с использованием набора фигур, обозначающих тип оператора, и называются схемами алгоритмов (программ).
Граф выявляет структуру алгоритма, определяя множество операторов V={V1 . . . , VК-1} и дуг D={(i,j)}, i=0, . . . ,K—1 и j =1, . . . , K, связывающих операторы. Для оценки трудоемкости ,алгоритма необходимо, во-первых, разбить множество операторов на классы: основных операторов S0={Vа1 . . . , Vаmо}, Vak, V, операторов ввода — вывода Sh = {V . . . , V }, h=1, . . . , H, (каждый и.ч этих операторов задает обращения к одному и тому же файлу Fн). Во-вторых, для каждого основного оператора Vа необходимо определить среднее количество операций ka, составляющих операторов, и для каждого оператора ввода — вывода V — среднее количество информации, передаваемой при выполнении оператора. В-третьих, переходы между операторами Vi и Vj следует рассматривать как случайные события и характеризовать их вероятностями рij т. е. каждая дуга графа алгоритма должна быть отмечена вероятностью перехода рij, с которой, переход из вершины выполняется именно по этой дуге, т. е. Так как вычислительный процесс не может приостановиться в вершине Vj с вероятностью 1 произойдет переход к какой-либо вершине графа алгоритма. С учетом этого вероятности переходов должны отвечать условию
![]()
Значения рij определяются вероятностями значений предикатов, зависящими от распределения значений данных, отношения между которыми задаются предикатами. Другими словами, вероятности рij , зависят от вероятностей выполнения условия, проверяемого оператором I с целью выбора пути перехода.
Пусть п1 ..., пк_1 — среднее число обращений к операторам V1 . . . , Vк_1 за один прогон алгоритма. В таком случае характеристики трудоемкости могут быть вычислены следующим образом:
v среднее число операций, выполняемых при одном прогоне алгоритма
|
|
|
v среднее число обращений к файлу Fн |
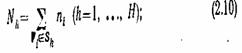
|
|
1.2.2 Модель вычислительной системы
ВС можно рассматривать как совокупность устройств, процессы функционирования которых являются процессами массового обслуживания, и для их описания используются модели теории массового обслуживания. Это одно- и многоканальные СМО.
Совокупность взаимосвязанных СМО называется стохастической сетью. Конфигурация сети отражает как структуру ВС, так и последовательность этапов вычислительного процесса, развивающегося в пределах этой структуры.
Для описания ВС используют стохастические сети разомкнутые и замкнутые. Для разомкнутой сети характерно, что интенсивность источника заявок не зависит от состояния сети, т.е. от числа заявок, уже поступивших в сеть. Для замкнутой сети интенсивность источника заявок зависит от состояния сети и числа заявок, циркулирующих в ней.
В данной работе в качестве моделей систем применяются разомкнутые сети, в которых может находиться на обработке переменное число заявок. В этом случае заявки имеют смысл запросов со стороны пользователей на выполнение определенных программ в ВС.
Стохастическая сеть определяется следующей совокупностью параметров:
1. Числом СМО, образующих сеть;
2. Числом каналов в составе каждой СМО;
3. Интенсивностью источника входных заявок на инициацию выполнения программ в ВС;
4. Матрицей вероятностей передач заявок из одной СМО в другую.
Передача заявок между СМО, входящими в стохастическую сеть можно представить ориентированным взвешенным графом передач заявок. Вес дуг графа определяется соответствующими элементами матрицы вероятности передач заявок в сети. Для разомкнутой стохастической сети по графу передач заявок можно построить систему алгебраических уравнений, выражающих соотношение интенсивностей потоков заявок между СМО сети в установившемся режиме. Из ее решения определяются интенсивности входных потоков заявок в каждую СМО, а значит становятся известными коэффициенты передач заявок между СМО сети.
По найденным интенсивностям и известным трудоемкостям обслуживания заявок в СМО можно рассчитать параметры всех СМО, входящих в сеть. На основе этих данных становятся расчетными характеристики всей стохастической сети:
v Среднее число заявок, ожидающих обслуживания в сети;
v Среднее число заявок, пребывающих в сети;
v Среднее число заявок в очередях;
v Среднее число заявок в сети;
v Среднюю загрузку систем сети;
v Среднее время ожидания в сети;
v Среднее время пребывания в сети;
v Время ответа ВС.
1.3 Формирование критерия оптимальности структуры вычислительной системы
Задача синтеза сводится к выбору таких значений параметров структуры, при которых ВС оказывается наилучшим образом приспособлена для решения заданного класса задач. Степень приспособленности, т.е. эффективности оценивается так. Выигрыш за счет малого времени решения задач в ВС должен соизмеряться с ценой потерь, возникающих из-за недогруза оборудования. Таким образом, характеристики ресурсов системы должны быть определенным образом сбалансированы с трудоемкостью выполняемых работ и темпом их поступления в систему. Степень сбалансированности системы "задачи-ВС" характеризуется посредством критерия сбалансированности, который строится следующим образом. Проектируемая ВС предназначена для решения r задач, поступающих на обработку с интенсивностями λ 1,… λr, и состоит из n устройств с ценами s1, …, sn и быстродействием V1, …, Vn соответственно. Программы каждого типа характеризуются определенными потребностями в ресурсах устройств 1,….n . Тогда задачу синтеза наиболее часто формулируют в одной из двух постановок [2]:
1. Синтезировать систему, обеспечивающую решение известного набора задач за минимально возможное время, причем стоимость системы не должна превышать заданного значения S*.
2. Синтезировать систему, обеспечивающую решение известного набора задач при среднем времени ответа системы, не превосходящем заданной величины U*, причем стоимость системы должна быть минимальной.
В данной работе принимается вторая постановка задачи синтеза, при решении которой необходимо найти параметры ресурсов ВС, которые обеспечивают решение заданного набора программ за заданное время при минимальной стоимости ресурсов ВС.
Критерий качества функционирования такой ВС можно представить в виде :
dG/dV = 0,
G = S + γ ( U - U* ),
S = ∑sk ,
U = ∑ αk * uk ,
U < U*
где
sk - стоимость к-ресурса;
uk - время использования к -ресурса при однократном обращении к нему заявки;
αk - коэффициент передач заявок между ресурсами ВС.
Общее решение полученной системы дает оптимальный набор параметров ресурсов ВС.
1.4 Выбор метода оптимизации
Процедура оптимизации предполагает поиск такого набора управляемых факторов модели исследуемого объекта (процесса) при котором достигается требуемое качество его функционирования, выражаемое целевой функцией. Искомый набор факторов может быть найден прямым перебором всех возможных вариантов комбинаций, из которых согласно вычисляемых значений целевой функции будет исследователем выбран наиболее подходящий (оптимальный).
Трудоемкость процедуры перебора вариантов при оптимизации зависит от полученной модели объекта. При ранжировании по снижению трудоемкости и стоимости работ по поиску оптимальных решений (но, одновременно, с пропорциональной потерей достоверности получаемых результатов) возможно использование следующих подходов:
v натурные эксперименты;
v имитационное моделирование множества режимов и структур оптимизируемой вычислительной системы;
v обобщающий математический анализ аналитической (а поэтому приближенной, упрощенной, линеаризованной) модели вычислительной системы с выполнением установленных ограничений и в соответствии с построенной целевой функцией;
v комбинация выше перечисленных подходов.
В данной работе используется оценочная аналитическая оптимизация параметров вычислительной системы в узком диапазоне изменений исходных факторов с последующим уточнением оптимальных параметров на имитационной модели.
Поэтому для процедуры оптимизации параметров вычислительной системы может быть использован подход Лагранжа [5], суть которого в следующем. Решая уравнение
dG/dV = 0,
находим выражение V=F(γ). Затем подстановкой V=F(γ) в U = U* находим выражение для расчета γ, подставив которое в V=F(γ) найдем окончательную формулу для расчета V. Подставляя его в S = ∑sk и в U = ∑ αk * uk , найдем фактическую стоимость системы и оптимальные значения параметров ВС, при которых обеспечивается минимум функции G = S + γ ( U - U* ).
1.5 Использование моделирования для оптимизации производительности сети
Для исследования реальных сетей используются анализаторы протоколов , но они не позволяют получать количественные оценки характеристик для еще не существующих сетей, находящихся в стадии проектирования. В таких случаях проектировщики могут использовать средства моделирования, с помощью которых разрабатываются модели, воссоздающие информационные процессы, протекающие в сетях.
Моделирование представляет собой мощный метод научного познания, при использовании которого исследуемый объект заменяется более простым объектом, называемым моделью. Основными разновидностями процесса моделирования можно считать два его вида - математическое и физическое моделирование. При физическом (натурном) моделировании исследуемая система заменяется соответствующей ей другой материальной системой, которая воспроизводит свойства изучаемой системы с сохранением их физической природы. Примером этого вида моделирования может служить пилотная сеть, с помощью которой изучается принципиальная возможность построения сети на основе тех или иных компьютеров, коммуникационных устройств, операционных систем и приложений.
Возможности физического моделирования довольно ограничены [18,19]. Оно позволяет решать отдельные задачи при задании небольшого количества сочетаний исследуемых параметров системы. Действительно, при натурном моделировании вычислительной сети практически невозможно проверить ее работу для вариантов с использованием различных типов коммуникационных устройств - маршрутизаторов, коммутаторов и т.п. Проверка на практике около десятка разных типов маршрутизаторов связана не только с большими усилиями и временными затратами, но и с немалыми материальными затратами.
Но даже и в тех случаях, когда при оптимизации сети изменяются не типы устройств и операционных систем, а только их параметры, проведение экспериментов в реальном масштабе времени для огромного количества всевозможных сочетаний этих параметров практически невозможно за обозримое время. Даже простое изменение максимального размера пакета в каком-либо протоколе требует переконфигурирования операционной системы в сотнях компьютеров сети, что требует от администратора сети проведения очень большой работы.
Поэтому, при оптимизации сетей во многих случаях предпочтительным оказывается использование математического моделирования [16]. Математическая модель представляет собой совокупность соотношений (формул, уравнений, неравенств, логических условий), определяющих процесс изменения состояния системы в зависимости от ее параметров, входных сигналов, начальных условий и времени.
Особым классом математических моделей являются имитационные модели. Такие модели представляют собой компьютерную программу, которая шаг за шагом воспроизводит события, происходящие в реальной системе. Применительно к вычислительным сетям их имитационные модели воспроизводят процессы генерации сообщений приложениями, разбиение сообщений на пакеты и кадры определенных протоколов, задержки, связанные с обработкой сообщений, пакетов и кадров внутри операционной системы, процесс получения доступа компьютером к разделяемой сетевой среде, процесс обработки поступающих пакетов маршрутизатором и т.д. При имитационном моделировании сети не требуется приобретать дорогостоящее оборудование - его работы имитируется программами, достаточно точно воспроизводящими все основные особенности и параметры такого оборудования.
Преимуществом имитационных моделей является возможность подмены процесса смены событий в исследуемой системе в реальном масштабе времени на ускоренный процесс смены событий в темпе работы программы. В результате за несколько минут можно воспроизвести работу сети в течение нескольких дней, что дает возможность оценить работу сети в широком диапазоне варьируемых параметров.
Результатом работы имитационной модели являются собранные в ходе наблюдения за протекающими событиями статистические данные о наиболее важных характеристиках сети: временах реакции, коэффициентах использования каналов и узлов, вероятности потерь пакетов и т.п.
Существуют специальные, ориентированные на моделирование вычислительных сетей программные системы, в которых процесс создания модели упрощен [14]. Такие программные системы сами генерируют модель сети на основе исходных данных о ее топологии и используемых протоколах, об интенсивностях потоков запросов между компьютерами сети, протяженности линий связи, о типах используемого оборудования и приложений. Программные системы моделирования могут быть узко специализированными и достаточно универсальными, позволяющие имитировать сети самых различных типов. Качество результатов моделирования в значительной степени зависит от точности исходных данных о сети, переданных в систему имитационного моделирования.
Программные системы моделирования сетей - инструмент, который может пригодиться любому администратору корпоративной сети, особенно при проектировании новой сети или внесении кардинальных изменений в уже существующую. Продукты данной категории позволяют проверить последствия внедрения тех или иных решений еще до оплаты приобретаемого оборудования. Конечно, большинство из этих программных пакетов стоят достаточно дорого, но и возможная экономия может быть тоже весьма ощутимой.
Программы имитационного моделирования сети используют в своей работе информацию о пространственном расположении сети, числе узлов, конфигурации связей, скоростях передачи данных, используемых протоколах и типе оборудования, а также о выполняемых в сети приложениях.
Обычно имитационная модель строится не с нуля. Существуют готовые имитационные модели основных элементов сетей: наиболее распространенных типов маршрутизаторов, каналов связи, методов доступа, протоколов и т.п. Эти модели отдельных элементов сети создаются на основании различных данных: результатов тестовых испытаний реальных устройств, анализа принципов их работы, аналитических соотношений. В результате создается библиотека типовых элементов сети, которые можно настраивать с помощью заранее предусмотренных в моделях параметров.
Системы имитационного моделирования обычно включают также набор средств для подготовки исходных данных об исследуемой сети - предварительной обработки данных о топологии сети и измеренном трафике. Эти средства могут быть полезны, если моделируемая сеть представляет собой вариант существующей сети и имеется возможность провести в ней измерения трафика и других параметров, нужных для моделирования. Кроме того, система снабжается средствами для статистической обработки полученных результатов моделирования.
В следующей таблице приведены характеристики нескольких популярных систем имитационного моделирования различного класса - от простых программ, предназначенных для установки на персональном компьютере, до мощных систем, включающих библиотеки большинства имеющихся на рынке коммуникационных устройств и позволяющих в значительной степени автоматизировать исследование изучаемой сети [12].
|
Компания и продукт |
Стоимость (долл) |
Тип сети |
Требуемые ресурсы |
Примечания |
|
American HYTech, Prophesy |
1495 |
ЛС |
8МбОП, 6 Мбдиск, DOS, Windows, OS/2 |
Оценивание производительности при работе с текстовыми и графическими данными по отдельным сегментам и сети в целом |
|
CACI Product, COMNET III |
34500-39500 |
ЛС, ГС |
32 МбОП, 100 Мбдиск, Windows, Windows NT, OS/2, Unix |
Моделируетсети X.25, ATM, Frame Relay, связи LAN-WAN, SNA, DECnet, протоколы OSPF, RIP. Доступ CSMA/CD и токенный доступ, FDDI и др. Встроенная библиотека марщрутизаторов 3COM, Cisco, DEC, HP, Wellfleat, ... |
|
Make System, NetMaker XA |
6995-14995 |
ЛС, ГС |
128 МбОП, 2000 Мбдиск, AIX, Sun OS, Sun Solaris |
Проверка данных о топологии сети; импорт информации о трафике, получаемой в реальном времени |
|
NetMagic System,StressMagik |
2995 |
ЛС |
2 МбОП, 8 МБдиск, Windows |
Поддержка стандартных тестов измерения производительности; имитация пиковой нагрузки на файл-сервер |
|
Network Analysis Center, MIND |
9400-70000 |
ГС |
8 MбОП, 65 Мбдиск, DOS, Windows |
Средство проектирования, оптимизации сети, содержит данные о стоимости типичных конфигураций с возможностью точного оценивания производительности |
|
Network Design and Analysis Group, AutoNet/ Designer |
25000 |
ГС |
8 MбОП, 40 Мбдиск, Windows, OS/2 |
Определение оптимального расположения концентратора в ГС, возможность оценки экономии средств за счет снижения тарифной платы, смены поставщика услуг и обновления оборудования; сравнение вариантов связи через ближайшую и оптимальную точку доступа, а также через мост и местную телефонную сеть |
|
Network Design and Analysis Group, AutoNet/ MeshNET |
30000 |
ГС |
8 MбОП, 40 Мбдиск, Windows, OS/2 |
Моделирование полосы пропускания и оптимизация расходов на организацию ГС путем имитации поврежденных линий, поддержка тарифной сетки компаний AT & T, Sprint, WiTel, Bell |
|
Network Design and Analysis Group, AutoNet/ Performance-1 |
4000 |
ГС |
8 MбОП, 1 Мбдиск, Windows, OS/2 |
Моделирование производительности иерархических сетей путем анализа чувствительности к длительности задержки, времени ответа, а также узких мест в структуре сети |
|
Network Design and Analysis Group, AutoNet/ Performance-3 |
6000 |
ГС |
8 MбОП, 3 Мбдиск, Windows, OS/2 |
Моделирование производительности многопротокольных объединений локальных и глобальных сетей; оценивание задержек в очередях, прогнозирование времени ответа, а также узких мест в структуре сети; учет реальных данных о трафике, поступающих от сетевых анализаторов |
|
System& Networks, BONES |
20000-40000 |
ЛС, ГС |
32 MбОП, 80 Мбдиск, Sun OS, Sun Solaris, HP-UX |
Анализ воздействия приложений клиент-сервер и новых технологий на работу сети |
|
MIL3,Opnet |
16000-40000 |
|
16 МбОП, 100 Мбдиск, DEC AXP, Sun OS, Sun Solaris, HP-UX |
Имеет библиотеку различных сетевых устройств, поддерживает анимацию, генерирует карту сети, моделирует полосу пропускания. |
Представленная здесь для сравнения Система имитационного моделирования COMNET позволяет анализировать работу сложных сетей, работающих на основе практически всех современных сетевых технологий и включающих как локальные, так и глобальные связи.
Существуют также системы имитационного моделирования, которые ориентируются на узкий класс изучаемых систем и позволяют строить модели без программирования.
Существуют также специальные языки имитационного моделирования, которые облегчают процесс создания программной модели по сравнению с использованием универсальных языков программирования. Примерами языков имитационного моделирования могут служить такие языки, как SIMULA, GPSS, SIMDIS [4, 18, 19, 9].
Язык GPSS относится к числу наиболее широко применяемых языков системного моделирования , что объясняется не его уникальными свойствами, а его распространенностью и наличием хорошо апробированных трансляторов [2].
Язык GPSS относят к универсальным языкам системного моделирования, хотя в наибольшей степени он приспособлен для описания систем с объектами информационной природы, таких как ВС и системы передачи данных. В составе языка определены структурные элементы типа устройство и память. Обладает средствами сбора статистики о ходе процессов в составе сети. Язык GPSS легок в усвоении и для его использования достаточно минимального опыта в программировании [2].
По этим причинам для разработки имитационной модели выбран язык GPSS.
1.6 Методика и задачи исследований
На основе графоаналитического представления ресурсов вычислительной системы и класса задач, решаемых в ней построить аналитические детерминированные линейные полнобазисные модели компонент вычислительных систем, найти и исследовать их многофакторную зависимость, на основании которой разработать методику поиска наилучших системных решений при реструктуризации существующих вычислительных сетей.
В плане выполнения исследований предполагается решить следующие задачи.
1. Разработать модель информационной связности комплекса программ, параллельно выполняемых при управлении предприятием, и определить параметры этого комплекса, являющиеся уже выходной характеристикой класса задач, решаемых в вычислительной системе.
2. Разработать модель для представления конкретной структуры (топологии и взаимосвязи ресурсов) вычислительной системы предприятия, для которой исходными и задающими расчет данными является полученная характеристика класса задач, решаемых в вычислительной системе.
3. Разработать схему расчета параметров вычислительного процесса в вычислительной системе при выполнении всего комплекса программ по управлению предприятием.
4. Найти аналитическую зависимость времени ответа системы от характеристик класса решаемых задач и параметров ресурсов вычислительной системы, на основе которой построить функцию цели для оптимизации параметров ресурсов вычислительной системы.
Выполнить сравнительные исследования результатов оптимизации вычислительной системы полученных с помощью построенной целевой функции и на имитационной GPSS-модел