IV. Способы кодирования на основе анализа временных
параметров
Целью цифрового
кодирования является возможно более точное
представление речевого сигнала для того, чтобы по этому цифровому представлению
можно было восстановить исходный акустический сигнал. Однако при решении многих
задач по обработке речи нас интересует не восстановление акустического
сигнала, а возможность его представления совокупностью свойств или параметров
модели, рассмотренной в разделе II. Ряд сравнительно простых, но также полезных
характеристик можно определить путем непосредственных измерений параметров
самого сигнала, а именно по его ИКМ-представлению.
Ключом к этим, а по сути
дела и ко всем параметрическим представлениям является понятие кратковременного
анализа. Из фиг. 2 видно, что если выбрать
произвольный участок речевого сигнала длительностью 10—30 ms,
то весьма вероятно, что свойства сигнала на таком интервале заметно не
изменятся. Можно, например, выбрать вокализированный участок, на котором
речевой сигнал характеризуется периодом основного тона и амплитудой. С другой
стороны, можно выбрать невокализированный участок, на
котором отсутствует периодичность сигнала, и нельзя говорить об амплитуде
участка в целом. Поскольку эти свойства изменяются от участка к участку, речь
принято анализировать на основе скользящего во времени базиса, выполняя анализ
коротких участков речи через равные промежутки времени.
Измерение пиков
Из фиг.
2 легко видеть, что на вокализированпых интервалах
речевой сигнал характеризуется последовательностью пиков, периодически
появляющихся с основной частотой речевого сигнала. В противоположность этому
на невокализированных интервалах пики имеют сравнительно
меньшую величину и их появление не имеет видимой закономерности. Таким
образом, максимальную амплитуду пика на анализируемом интервале можно
использовать и в качестве простого индикатора амплитуды сигнала, и как
средство для различения вокализированных и невокализированных участков речи
Временной интервал между
соответствующими пиками, очевидно, равен основному периоду вокализированной
речи. Этот принцип положен в основу многочисленных способов определения
основного периода или периода основного тона. Однако главная трудность здесь в
том, что даже на весьма коротких временных интервалах
речевой сигнал не имеет строго периодической структуры. Поскольку на каждом периоде
имеется множество пиков, возможно несколько различных оценок этого периода.
Способ логического объединения результатов нескольких простых замеров такого
рода для повышения точности описан Голдом и Рабииером. Путем тщательного выбора элементарных
измерителей и схемы логической обработки удается получить существенный выигрыш
в точности суммарной оценки по отношению к любой из отдельных оценок.
Измерения энергии
Одним из простейших
представлений сигнала является его энергия. Энергия вещественного дискретного
во времени сигнала
 (4)
(4)
Для
нестационарных сигналов, например речевого, более удобно вычислять изменяющуюся
во времени энергию в виде
 (5)
(5)
где w (m) —
весовая последовательность или окно, которое выделяет участок х (n), a
N — количество отсчетов в окне. В простейшем случае, когда
для всех т функция w(m)=1, энергия Е (n)
равна сумме квадратов N последних значений сигнала х
(n). На фиг. 7, а представлен один из
способов измерения энергии (5) посредством сглаживания последовательности х(n) фильтром с конечной
длительностью импульсной реакции вида W (n).
Как и следовало ожидать,
функция E(n) отображает изменяющиеся во времени
амплитудные свойства речевого сигнала. Однако определение (5) нуждается в
тщательной интерпретации. Во-первых, это касается выбора окна. Задача окна
состоит в приписывании меньших весов более старым отсчетам речи, поэтому с
увеличением m w(m),
как правило, монотонно стремится к нулю. Если на всем интервале отсчеты должны
иметь одинаковый вес, используется прямоугольное окно. Вторая трудность
заключается в выборе интервала измерения N. При слишком малом N, когда его величина
меньше периода основного тона, величина энергии Е (n), определяемой выражением
(5), подвержена быстрым флуктуациям, зависящим от тонкой структуры сигнала.
Если N слишком велико и равно нескольким периодам основного тона, величина Е (n)
изменяется незначительно и поэтому не может отразить изменяющиеся свойства
речевого сигнала. Практически наиболее подходящее значение N при частоте
дискретизации 10 kHz составляет величину порядка 100—200 (т.
е. 10—20 ms речи).
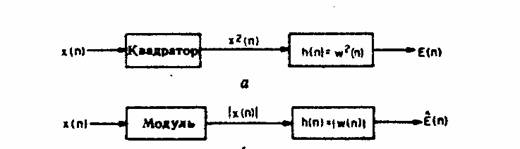
Фмг. 7. а
— способ вычисления кратковременной энергий при использования цифрового фильтра
с конечной длительностыо импульсной реакции; 6 - еще
один способ определения энергяи.
Основное значение
энергии Е (n) состоит в том, что она может служить хорошей мерой отличия
вокализированных и невокализированных участков речи. Как можно видеть из фиг.
2, на невокализированных участках величина Е(n) намного меньше, чем для вокализированных. Кроме того, чем меньше N,
тем меньше ошибка определения точного положения границ, где невокализированная
речь переходит а вокализировапную
и обратно. Более того, применительно к высококачественной речи энергию можно
использовать для отделения невокализированных участков речи от паузы.
t
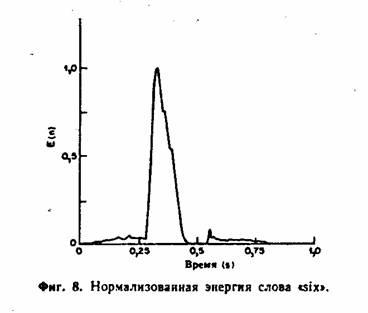
Процедура измерения
энергии осложняется тем обстоятельством, что ее величина сильно изменяется при
больших уровнях сигнала в (5) величина уровня возводится
в квадрат, усиливая тем самым в Е (n) большие перепады между
отсчетами. Один из сравнительно простых способов преодоления этой трудности
состоит в том, что для оценки энергии используют функцию
в которой вместо суммы квадратов вычисляют сумма абсолютных величии. На фиг. 7, это выражение интерпретировано в виде операции
линейной фильтрации по отношению к |x(n)|.
На фиг. 8 показана энергетическая функция слова «six» при использовании
прямоугольного окна длительностью 10 ms. Легко видеть, что на участках
фрикативных звуков в начале и в конце этого слова энергия имеет малую величину,
а во время смычки на звуке <k> она уменьшается
почти до нуля. Примером приложения энергетических измерений для распознавания
речи может служить работа Редди [14].
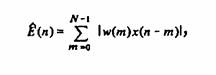
Измерены числа переходов через ноль.
Еще один весьма простой
способ анализа временных параметров сигнала основан на измерении числа переходов
через нуль. Имея в виду цифровое представление сигнала, можно утверждать, что
между моментами взятия n-го и (n — 1)-го
отсчетов произошло пересечение нулевого уровня, если
sign [х(n)] ¹ sign [(n - 1)] (7)
Это измерение несложно в
реализации и часто используется для грубой оценки частотного содержания
речевого сигнала. Возможность его использования объясняется тем, что для
синусоидального сигнала с частотой f среднее число
пересечений нулевого уровня в 1 s равно
n=2f0 (8)
Однако соотношение (8)
нельзя без оговорок распространить на речевой сигнал, поскольку большая часть
звуков речи имеет широкий спектр частот. Тем не менее
иногда достаточно даже такой грубой оценки.
Например, хорошо
известно, что энергия вокализированной речи обычно концентрируется в диапазоне
ниже 3 kHz, тогда как энергия фрикативных звуков в основном
сосредоточена выше 3 kHz. На этом основании результаты
измерений числа переходов через нуль (наряду с информацией об энергии) часто
используются для принятия решения о том, вокализированный
или невокалнзнрованный характер имеет данный
участок речи. Если частота пересечений высока, то это свидетельствует о невокализироваином характере речи, если же она мала, то
весьма вероятно, что анализируется вокализированный участок. В сочетании с детектором основного тона речи измерения числа переходов
через нуль оказываются весьма полезными при оценке параметров возбуждения [341.
Они также успешно применяются для представления речевых сигналов при решении
задачи по распознаванию речи [14].
При цифровой реализации
измерений числа переходов через нуль следует учитывать ряд важных обстоятельств.
Хотя в соответствии с основным алгоритмом требуется произвести лишь сравнение
знаков двух следующих друг за другом отсчетов, необходимо также весьма
тщательно выполнять и саму процедуру дискретизации. Большие искажения в
результаты измерений числа переходов через нуль вносят наличие шума, смещение
уровня постоянного тока и напряжение фона с частотой питающей сети 60 Hz.
Поэтому для ослабления мешающего влияния указанных факторов перед устройством
дискретизации вместо фильтра нижних частот ставится полосовой фильтр. Кроме
того, поскольку временное разрешение при измерении числа переходов через нуль
определяется периодом дискретизации Т, его повышение сопряжено с увеличением
частоты дискретизации. Вместе с тем для неискаженной передачи информации о
числе переходов через нуль можно применить чрезвычайно грубое двухуровневое
квантование.
Кратковременный автокорреляционный анализ.
Функция автокорреляции
дискретного во времени сигнала х(n)
определяется как
 (9)
(9)
Автокорреляционная
функция весьма полезна для выявления структуры любого сигнала, и в этом смысле
речь не составляет исключения. Если, например, некоторый сигнал имеет
периодическую структуру с периодом Р. т. е. x(n+Р)=х (n) для всех n, то
легко показать, что
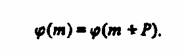 (10)
(10)
Таким образом,
периодичность автокорреляционной функции указывает на периодичность исходного
сигнала. С другой стороны, если автокорреляционная функция в окрестности точки
m=0 имеет острый пик и с возрастанием m
быстро спадает к нулю, то это указывает на отсутствие в сигнале предсказуемой
структуры.
Как уже отмечалось, речь
является нестационарным сигналом. Однако в течение сравнитетельно длинных интервалов времени свойства речевого
сигнала сохраняются неизменными.. Как мы уже видели. это свойство служит основой кратковременного анализа, т. е.
анализа коротких участков речевого сигнала. Рассмотрим для примера отрезок
сигнала из N отсчетов
![]() (11)
(11)
где через l
обозначено начало этого отрезка. В этом. случае кратковременная автокорреляционная функция может
быть определена как
![]() (12)
(12)
где через M0, обозначена максимально
требуемая задержка. Так, например, для выявления периодичности сигнала
необходимо выполнить условие М,>Р. Значение целого числа N’
оговорено ниже.
Выражение [11] можно трактовать как
автокорреляцию отрезка речевого сигнала протяженностью в N отсчетов, начиная с
отсчета I. Если N'=N. то для вычисления
используются отсчеты, находящиеся вне отрезка l<n<N+l-1.
Если N'=N - m,
то используются отсчеты только внутри интервала. В последнем случае
исследуемый отрезок часто взвешивается с помощью функции «окна», которая
плавно сводит к нулю величины отсчетов на концах отрезка. При использовании
автокорреляционной функции для обнаружения периодичности в
речевом сигнале подходит любая функция «окна», однако, как будет показано в
разделе VII, правильный выбор «окна» имеет большое значение для анализа на
основе линейного предсказания. В любом случае прямое вычисление jl(m) для 0<m<M0 - 1 связано с затратами
машинного времени, пропорциональными величине M0N, а это может оказаться
невыгодным.
Способы кратковременного
анализа используются, как правила, для оценки параметров речевой модели, рассмотреной в разделе II. Обычно предполагается, что для
хранения существенных признаков речевого сигнала при его кодировании с помощью
ИКМ может потребоваться частота дискретизации от 6 до 20 kHz,
однако кодирование медленно изменяющихся параметров модели возможно со
значительно меньшей частотой (от 50 до 100 Hz). Положим для примера,
что частота дискретизации речевого сигнала равна 10 kHz, а кратковременная
автокорреляция должна вычисляться 100 раз в секунду. Оценка величины
автокорреляции обычно производится на отрезках речевого сигнала длительностью
20—40 ms (для оценки периодичности сигнала длительность окна должна
быть достаточной для перекрытия минимум двух периодов речевого сигнала). Таким
образом, при частоте дискретизации 10 kHz количество отсчетов находится
в интервале 200<N<400, а требуемые оценки величины
автокорреляции должны вычисляться для приращения, равного 100 отсчетам.
При использовании
кратковременной автокорреляционной функции для оценки периода основного тона
желательно, чтобы эта функция имела острые пики с интервалом, кратным периоду
Р. Корреляционная функция речи не имеет острых пиков, поскольку структуру
каждого периода речевого сигнала в значительной степени можно предсказать
заранее. Несколько способов построения пиков автокорреляционной функции было
предложено Сондхи 151. Один из них, получивший
название способа центрального клиппирования
(вырезания), иллюстрируется фиг. 9. Нелинейная
операция вырезания средней (по амплитуде) части речевого сигнала позволила
существенно ослабить корреляцию между дискретными отсчетами сигнала. Это
иллюстрируется фиг. 10, на которой показана
последовательность кратковременных функций автокорреляции, вычисленных с
интервалом 15 ms (частота дискретизации равна 66 Hz)
на отрезках центрально - клиппированной речи
длительностью 30 ms.
По серии таких
корреляционных функций можно оценить период основного тона путем простой
фиксации положения наиболее выраженного пика, который, очевидно, появляется на
участках вокализированиой речи. Соидхн
предложил алгоритм принятия решения, который позволяет формализовать этот
процесс. Он показал, что предложенная схема надежно работает либо на
вокализированных участках речи, когда форма сигнала близка к
синусоидальной, либо при отсутствии в сигнале основной частоты.


Фиг 10. – образцы
автокорреляционной функции